|
Homotopy Analysis Method
The homotopy analysis method (HAM) is a semi-analytical technique to solve nonlinear ordinary/partial differential equations. The homotopy analysis method employs the concept of the homotopy from topology to generate a convergent series solution for nonlinear systems. This is enabled by utilizing a homotopy-Maclaurin series to deal with the nonlinearities in the system. The HAM was first devised in 1992 by Liao Shijun of Shanghai Jiaotong University in his PhD dissertation and further modified in 1997 to introduce a non-zero auxiliary parameter, referred to as the convergence-control parameter, ''c''0, to construct a homotopy on a differential system in general form. The convergence-control parameter is a non-physical variable that provides a simple way to verify and enforce convergence of a solution series. The capability of the HAM to naturally show convergence of the series solution is unusual in analytical and semi-analytic approaches to nonlinear partial differential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Put Option
In finance, a put or put option is a derivative instrument in financial markets that gives the holder (i.e. the purchaser of the put option) the right to sell an asset (the ''underlying''), at a specified price (the ''strike''), by (or on) a specified date (the '' expiry'' or ''maturity'') to the ''writer'' (i.e. seller) of the put. The purchase of a put option is interpreted as a negative sentiment about the future value of the underlying stock. page 15 , 4.2.3 Positive and negative sentiment The term "put" comes from the fact that the owner has the right to "put up for sale" the stock or index. Puts may also be combined with other derivatives as part of more complex investment strategies, and in particular, may be useful for hedging. Holding a European put option is equivalent to holding the corresponding call option and selling an appropriate forward contract. This equivalence is called " put-call parity". Put options are most commonly used in the stock market to prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Limit Cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912). Definition We consider a two-dimensional dynamical system of the form x'(t)=V(x(t)) where V : \R^2 \to \R^2 is a smooth function. A ''trajectory'' of this system is some smooth function x(t) with values in \mathbb^2 which satisfies this differential equation. Such a trajectory is called ''closed'' (or ''periodic'') if it is not constant but returns to its starting point, i.e. if there exists some t_0>0 such that x(t + t_0) = x(t) for all t \in \R. An orbit (dynamics), orbit is the ima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
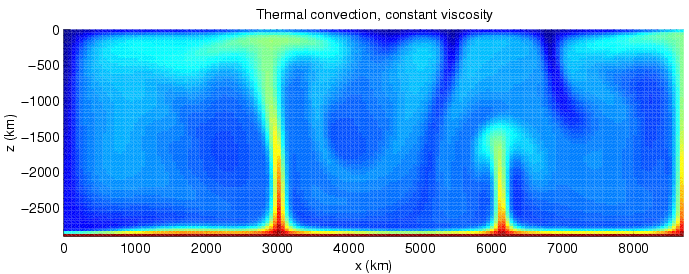
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gravity Waves
In fluid dynamics, gravity waves are waves in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves. A gravity wave results when fluid is displaced from a position of equilibrium. The restoration of the fluid to equilibrium will produce a movement of the fluid back and forth, called a ''wave orbit''. Gravity waves on an air–sea interface of the ocean are called surface gravity waves (a type of surface wave), while gravity waves that are the body of the water (such as between parts of different densities) are called '' internal waves''. Wind-generated waves on the water surface are examples of gravity waves, as are tsunamis, ocean tides, and the wakes of surface vessels. The period of wind-generated gravity waves on the free surface of the Earth's ponds, lakes, seas and oceans are predominantly b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wave Resonance
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. ''Periodic waves'' oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a ''standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. There are two types of waves that are most commonly studied in classical physics: mechanical waves and electromagnetic waves. In a mechanical wave, stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (strain) in some physical medium that propagates from particle to particle by creating local stresses that cause strain in neighboring particles too. For exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numerical Continuation
Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations, :F(\mathbf u,\lambda) = 0. The parameter \lambda is usually a real scalar and the ''solution'' \mathbf u is an ''n''-vector. For a fixed parameter value \lambda, F(\cdot,\lambda) maps Euclidean n-space into itself. Often the original mapping F is from a Banach space into itself, and the Euclidean n-space is a finite-dimensional Banach space. A steady state, or fixed point, of a parameterized family of flows or maps are of this form, and by discretizing trajectories of a flow or iterating a map, periodic orbits and heteroclinic orbits can also be posed as a solution of F=0. Other forms In some nonlinear systems, parameters are explicit. In others they are implicit, and the system of nonlinear equations is written :F(\mathbf u) = 0 where \mathbf u is an ''n''-vector, and its image F(\mathbf u) is an ''n-1'' vector. This formulation, without an explicit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Boundary Element Method
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations (i.e. in ''boundary integral'' form), including fluid mechanics, acoustics, electromagnetics (where the technique is known as method of moments or abbreviated as MoM), fracture mechanics, and contact mechanics. Mathematical basis The integral equation may be regarded as an exact solution of the governing partial differential equation. The boundary element method attempts to use the given boundary conditions to fit boundary values into the integral equation, rather than values throughout the space defined by a partial differential equation. Once this is done, in the post-processing stage, the integral equation can then be used again to calculate numerically the solution directly at any desired point in the interior of the solution domain. BEM is applicable to problems for which Green's functions can be calculated. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |