|
Generatrices
In geometry, a generatrix () or describent is a point, curve or surface that, when moved along a given path, generates a new shape. The path directing the motion of the generatrix motion is called a directrix or dirigent. Examples A cone can be generated by moving a line (the generatrix) fixed at the future apex of the cone along a closed curve (the directrix); if that directrix is a circle perpendicular to the line connecting its center to the apex, the motion is rotation around a fixed axis and the resulting shape is a circular cone. The generatrix of a cylinder, a limiting case of a cone, is a line that is kept parallel to some axis. See also * Surface of revolution A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ... References Elementary geometry Computer graphics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In geometry, a point is an abstract idealization of an exact position, without size, in physical space, or its generalization to other kinds of mathematical spaces. As zero-dimensional objects, points are usually taken to be the fundamental indivisible elements comprising the space, of which one-dimensional curves, two-dimensional surfaces, and higher-dimensional objects consist. In classical Euclidean geometry, a point is a primitive notion, defined as "that which has no part". Points and other primitive notions are not defined in terms of other concepts, but only by certain formal properties, called axioms, that they must satisfy; for example, ''"there is exactly one straight line that passes through two distinct points"''. As physical diagrams, geometric figures are made with tools such as a compass, scriber, or pen, whose pointed tip can mark a small dot or prick a small hole representing a point, or can be drawn across a surface to represent a curve. A po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is €¦the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which €¦will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface (mathematics)
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line. There are several more precise definitions, depending on the context and the mathematical tools that are used for the study. The simplest mathematical surfaces are planes and spheres in the Euclidean 3-space. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a topological space of dimension two; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a '' coordinate patch'' on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape
A shape is a graphics, graphical representation of an object's form or its external boundary, outline, or external Surface (mathematics), surface. It is distinct from other object properties, such as color, Surface texture, texture, or material type. In geometry, ''shape'' excludes information about the object's Position (geometry), position, size, Orientation (geometry), orientation and chirality. A ''figure'' is a representation including both shape and size (as in, e.g., figure of the Earth). A plane shape or plane figure is constrained to lie on a ''plane (geometry), plane'', in contrast to ''solid figure, solid'' 3D shapes. A two-dimensional shape or two-dimensional figure (also: 2D shape or 2D figure) may lie on a more general curved ''surface (mathematics), surface'' (a two-dimensional space). Classification of simple shapes Some simple shapes can be put into broad categories. For instance, polygons are classified according to their number of edges as triangles, qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
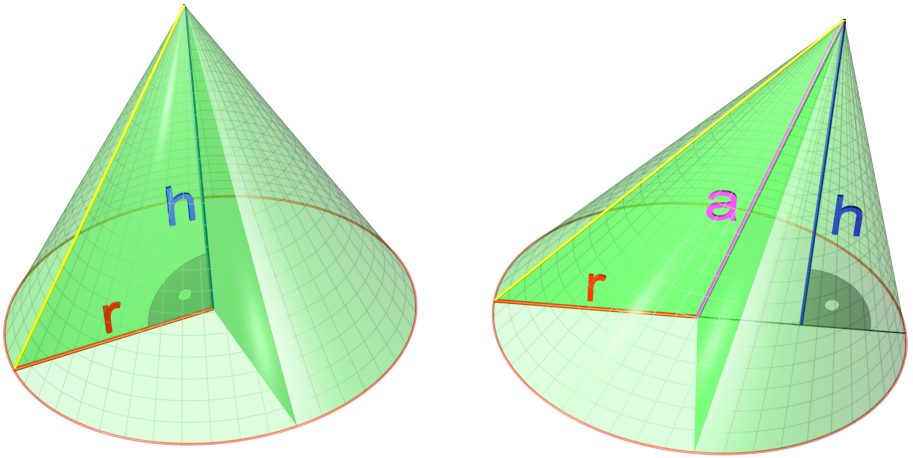
Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Around A Fixed Axis
Rotation around a fixed axis or axial rotation is a special case of rotational motion around an ''axis of rotation'' fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation (geometry), orientation and cannot describe such phenomena as nutation, wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result. This concept assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics (mechanics), dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for Rigid body dynamics#Rigid-body angular momentum, free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylinder (geometry)
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the '' right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel (geometry)
In geometry, parallel lines are coplanar infinite straight line (geometry), lines that do not intersecting lines, intersect at any point. Parallel planes are plane (geometry), planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not tangent, touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Line segments and Euclidean vectors are parallel if they have the same direction (geometry), direction or opposite direction (geometry), opposite direction (not necessarily the same length). Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometry, affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Of Revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersecting the generatrix, except at its endpoints). The volume bounded by the surface created by this revolution is the ''solid of revolution''. Examples of surfaces of revolution generated by a straight line are cylinder (geometry), cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |