|
Fractals
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called Affine geometry, affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they Scaling (geometry), scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractals In Technology
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Fractals By Hausdorff Dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension." Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to illustrate what it means for a fractal to have a low or a high dimension. Deterministic fractals Random and natural fractals See also * Fractal dimension * Hausdorff dimension * Scale invariance Notes and references Further reading * * * * External links The fractals on MathworldOther fractals on Paul Bourke's websiteFractals on mathcurve.com* ttps://web.archive.org/web/20060923100014/http://library.thinkquest.org/26242/full/index.html Fractals unleashedIFStile - software that computes the dimension of the boundary of self-affine tiles {{DEFAULTSORT:Fractals By Hausdorff Dimension Hausdorff Dimension Hausdorff Dimension In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Dimension
In mathematics, more specifically in fractal geometry, a fractal dimension is a ratio providing a statistical index of complexity comparing how detail in a pattern (strictly speaking, a fractal pattern) changes with the scale at which it is measured. It has also been characterized as a measure of the space-filling capacity of a pattern that tells how a fractal scales differently from the space it is embedded in; a fractal dimension does not have to be an integer. The essential idea of "fractured" dimensions has a long history in mathematics, but the term itself was brought to the fore by Benoit Mandelbrot based on his 1967 paper on self-similarity in which he discussed ''fractional dimensions''. In that paper, Mandelbrot cited previous work by Lewis Fry Richardson describing the counter-intuitive notion that a coastline's measured length changes with the length of the measuring stick used ( see Fig. 1). In terms of that notion, the fractal dimension of a coastline quantifie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Curve
A fractal curve is, loosely, a mathematical curve whose shape retains the same general pattern of irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fractal. In general, fractal curves are nowhere rectifiable curves — that is, they do not have finite length — and every subarc longer than a single point has infinite length. A famous example is the boundary of the Mandelbrot set. Fractal curves in nature Fractal curves and fractal patterns are widespread, in nature, found in such places as broccoli, snowflakes, feet of geckos, frost crystals, and lightning bolts. See also Romanesco broccoli, dendrite crystal, trees, fractals, Hofstadter's butterfly, Lichtenberg figure, and self-organized criticality. Dimensions of a fractal curve Most of us are used to mathematical curves having dimension one, but as a general rule, fractal curves have different dimensions, also see also fractal dimension and list of fractals by Hausdor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractals In Nature
Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time. In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Menger Sponge
In mathematics, the Menger sponge (also known as the Menger cube, Menger universal curve, Sierpinski cube, or Sierpinski sponge) is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension. Construction The construction of a Menger sponge can be described as follows: # Begin with a cube. # Divide every face of the cube into nine squares, like Rubik's Cube. This sub-divides the cube into 27 smaller cubes. # Remove the smaller cube in the middle of each face, and remove the smaller cube in the center of the more giant cube, leaving 20 smaller cubes. This is a level-1 Menger sponge (resembling a void cube). # Repeat steps two and three for each of the remaining smaller cubes, and continue to iterate ''ad infinitum''. The second iteration gives a level-2 sponge, the third iteration gives a level-3 sponge, and s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Dimension
In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that was first introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
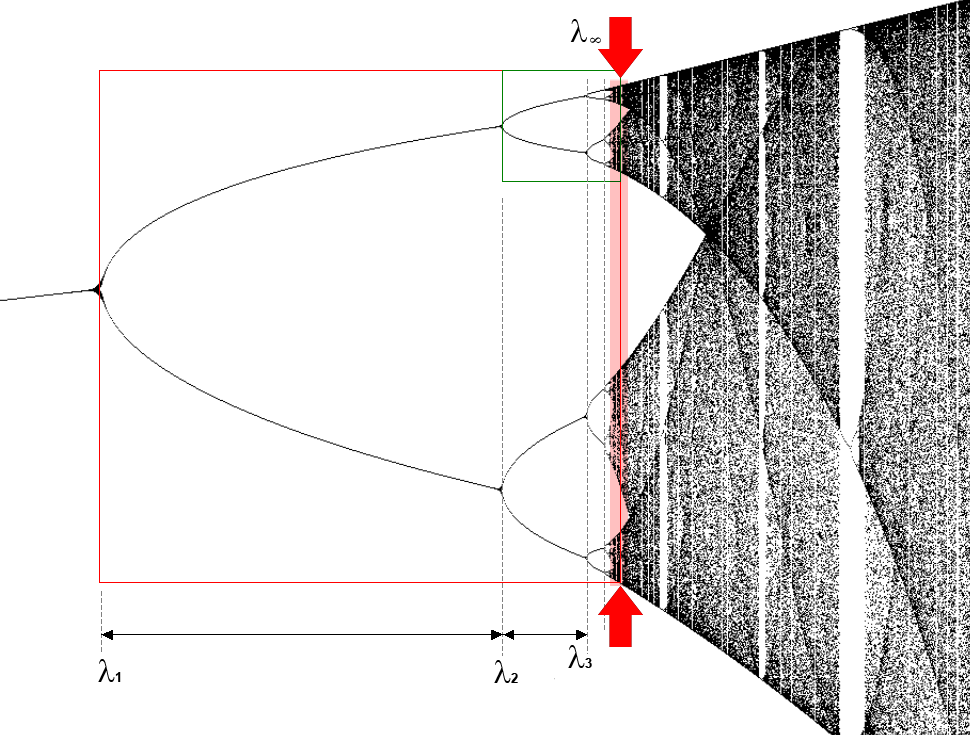
Mandelbrot Set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value. This set was first defined and drawn by Robert W. Brooks and Peter Matelski in 1978, as part of a study of Kleinian groups. Afterwards, in 1980, Benoit Mandelbrot obtained high-quality visualizations of the set while working at IBM's Thomas J. Watson Research Center in Yorktown Heights, New York. Images of the Mandelbrot set exhibit an elaborate and infinitely complicated boundary that reveals progressively ever-finer recursive detail at increasing magnifications; mathematically, one would say that the boundary of the Mandelbrot set is a ''fractal curve''. The "style" of this recursive detail depends on the region of the set boundary being examined. Mandelbrot set images may be created by sampling the complex numbers and testing, for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-similarity
__NOTOC__ In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales. Self-similarity is a typical property of fractals. Scale invariance is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar to the whole. For instance, a side of the Koch snowflake is both symmetrical and scale-invariant; it can be continually magnified 3x without changing shape. The non-trivial similarity evident in fractals is distinguished by their fine structure, or detail on arbitrarily small scales. As a counterexample, whereas any portion of a straight line may resemble the whole, further detail is not revealed. A time developing phenomenon is said to exhibit self-similarity if the numerical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. In mathematics and computer science, iteration (along with the related technique of recursion) is a standard element of algorithms. Mathematics In mathematics, iteration may refer to the process of iterating a function, i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviors and difficult problems – for examples, see the Collatz conjecture and juggler sequences. Another use of iteration in mathematics is in iterative methods which are used to produce approximate numerical solutions to certain mathematical problems. Newton's method is an example of an iterative method. Manual calculation of a number's square root is a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





.jpg)

