|
Fundamental Domain
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits. There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile the space. One general construction of fundamental domains uses Voronoi cells. Hints at a general definition Given an action of a group ''G'' on a topological space ''X'' by homeomorphisms, a fundamental domain for this action is a set ''D'' of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a topological space is a Set (mathematics), set whose elements are called Point (geometry), points, along with an additional structure called a topology, which can be defined as a set of Neighbourhood (mathematics), neighbourhoods for each point that satisfy some Axiom#Non-logical axioms, axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate. A topological space is the most general type of a space (mathematics), mathematical space that allows for the definition of Limit (mathematics), limits, Continuous function (topology), continuity, and Connected space, connectedness. Common types ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group Theory)
In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of R''n'', this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood. The theory is particularly rich for lattices in semisimple Lie groups or more generally in semisimple algebraic groups over local fields. In particular there is a wealth of rigidity results in this setting, and a celebrated theorem of Grigory Margulis states that in most cases all lattices are obtained as arithmetic groups. Lattices are also well-studied in some other classes of groups, in particular groups associated to Kac–Moody algebras and automorphisms groups of regular trees (the latter are known as ''tree lattices''). Lattices are of i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper Half-plane
In mathematics, the upper half-plane, is the set of points in the Cartesian plane with The lower half-plane is the set of points with instead. Arbitrary oriented half-planes can be obtained via a planar rotation. Half-planes are an example of two-dimensional half-space. A half-plane can be split in two quadrants. Affine geometry The affine transformations of the upper half-plane include # shifts (x,y)\mapsto (x+c,y), c\in\mathbb, and # dilations (x,y)\mapsto (\lambda x,\lambda y), \lambda > 0. Proposition: Let and be semicircles in the upper half-plane with centers on the boundary. Then there is an affine mapping that takes A to B. :Proof: First shift the center of to Then take \lambda=(\text\ B)/(\text\ A) and dilate. Then shift to the center of Inversive geometry Definition: \mathcal := \left\ . can be recognized as the circle of radius centered at and as the polar plot of \rho(\theta) = \cos \theta. Proposition: in and are collinear points. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Group
In mathematics, the modular group is the projective special linear group \operatorname(2,\mathbb Z) of 2\times 2 matrices with integer coefficients and determinant 1, such that the matrices A and -A are identified. The modular group acts on the upper-half of the complex plane by linear fractional transformations. The name "modular group" comes from the relation to moduli spaces, and not from modular arithmetic. Definition The modular group is the group of fractional linear transformations of the complex upper half-plane, which have the form :z\mapsto\frac, where a,b,c,d are integers, and ad-bc=1. The group operation is function composition. This group of transformations is isomorphic to the projective special linear group \operatorname(2,\mathbb Z), which is the quotient of the 2-dimensional special linear group \operatorname(2,\mathbb Z) by its center \. In other words, \operatorname(2,\mathbb Z) consists of all matrices :\begin a & b \\ c & d \end where a,b, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wallpaper Group
A wallpaper group (or plane symmetry group or plane crystallographic group) is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetry, symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tiles, and wallpaper. The simplest wallpaper group, Group ''p''1, applies when there is no symmetry beyond simple translation of a pattern in two dimensions. The following patterns have more forms of symmetry, including some rotational and reflectional symmetries: Image:Wallpaper_group-p4m-2.jpg, Example A: Cloth, Tahiti Image:Wallpaper_group-p4m-1.jpg, Example B: Ornamental painting, Nineveh, Assyria Image:Wallpaper_group-p4g-2.jpg, Example C: Painted porcelain, China Examples A and B have the same wallpaper group; it is called #Group p4mm, ''p''4''m'' in the International Union of Crystallography#IUCr Symmetry notation, IUCr notation and #Group p4mm, *442 in the orbifold notation. Example C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voronoi Diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation. The Voronoi diagram is named after mathematician Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi cells are also known as Thiessen polygons, after Alfred H. Thiessen. Voronoi diagrams have practical and theoretical applications in many fields, mainly in science and technology, but also in visual art. Simplest case In the simplest case, shown in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
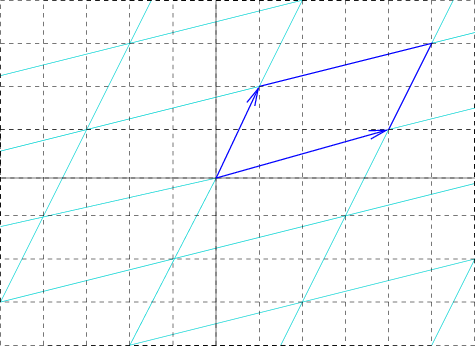
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. Three equivalent definitions of ''parallelepiped'' are *a hexahedron with three pairs of parallel faces, *a polyhedron with six faces (hexahedron), each of which is a parallelogram, and *a prism (geometry), prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all special cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; traditionally it was because of its etymology in Ancient Greek, Greek παραλληλεπίπεδον ''parallelepipedon'' (with short -i-), a body "having parallel planes". Parallelepipeds are a subclass of the prismatoids. Properties Any of the three pairs of parallel faces can be viewed as the bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Translational Symmetry
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation. Analogously, an operator on functions is said to be ''translationally invariant'' with respect to a translation operator T_\delta if the result after applying doesn't change if the argument function is translated. More precisely it must hold that \forall \delta \ A f = A (T_\delta f). Laws of physics are translationally invariant under a spatial translation if they do not distinguish different points in space. According to Noether's theorem, space translational symmetry of a physical system is equivalent to the momentum conservation law. Translational symmetry of an object means that a particular translation does not change the object. For a given object, the translations for which this applies form a group, the symmetry group of the object, or, if the obj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |