|
Fermi Level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics. In band structure theory, used in solid state physics to analyze the energy levels in a solid, the Fermi level can be considered to be a hypothetical energy level of an electron, such that at thermodynamic equilibrium this energy level would have a ''50% probability of being occupied at any given time''. The position of the Fermi level in relation to the band energy levels is a crucial factor in determining electrical properties. The Fer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid-state Physics
Solid-state physics is the study of rigid matter, or solids, through methods such as solid-state chemistry, quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from their atomic-scale properties. Thus, solid-state physics forms a theoretical basis of materials science. Along with solid-state chemistry, it also has direct applications in the technology of transistors and semiconductors. Background Solid materials are formed from densely packed atoms, which interact intensely. These interactions produce the mechanical (e.g. hardness and Elasticity (physics), elasticity), Heat conduction, thermal, Electrical conduction, electrical, Magnetism, magnetic and Crystal optics, optical properties of solids. Depending on the material involved and the conditions in which it was formed, the atoms may be arranged in a regular, geometric patt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
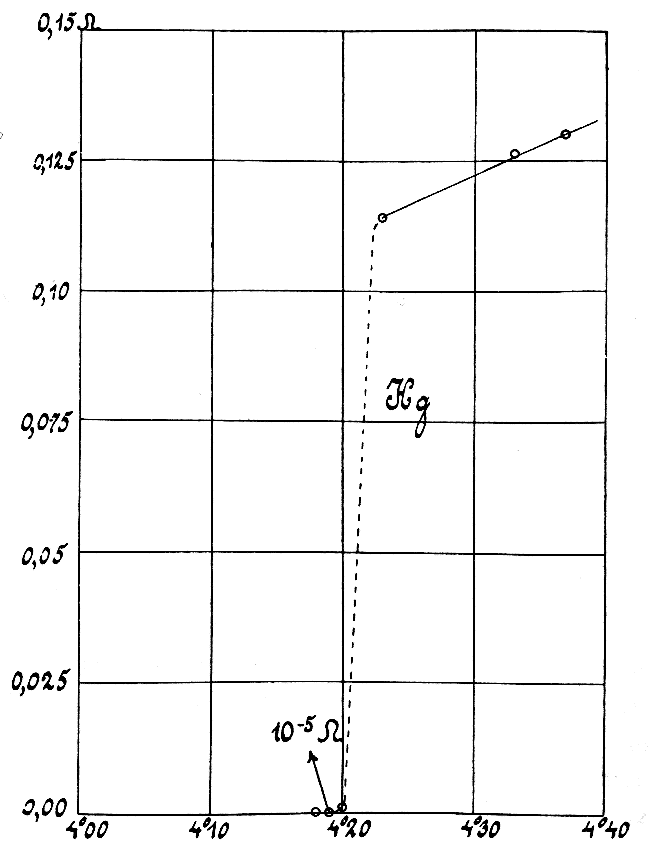
Short Circuit
A short circuit (sometimes abbreviated to short or s/c) is an electrical circuit that allows a current to travel along an unintended path with no or very low electrical impedance. This results in an excessive current flowing through the circuit. The opposite of a short circuit is an open circuit, which is an infinite resistance (or very high impedance) between two nodes. Definition A short circuit is an abnormal connection between two nodes of an electric circuit intended to be at different voltages. This results in an electric current limited only by the Thévenin equivalent resistance of the rest of the network which can cause circuit damage, overheating, fire or explosion. Although usually the result of a fault, there are cases where short circuits are caused intentionally, for example, for the purpose of voltage-sensing crowbar circuit protectors. In circuit analysis, a ''short circuit'' is defined as a connection between two nodes that forces them to be at the sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Effect Transistor
The field-effect transistor (FET) is a type of transistor that uses an electric field to control the current through a semiconductor. It comes in two types: junction FET (JFET) and metal-oxide-semiconductor FET (MOSFET). FETs have three terminals: ''source'', ''gate'', and ''drain''. FETs control the current by the application of a voltage to the gate, which in turn alters the conductivity between the drain and source. FETs are also known as unipolar transistors since they involve single-carrier-type operation. That is, FETs use either electrons (n-channel) or holes (p-channel) as charge carriers in their operation, but not both. Many different types of field effect transistors exist. Field effect transistors generally display very high input impedance at low frequencies. The most widely used field-effect transistor is the MOSFET (metal–oxide–semiconductor field-effect transistor). History The concept of a field-effect transistor (FET) was first patented by the Aust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity or those in a spring. The term ''potential energy'' was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to the ancient Greek philosopher Aristotle's concept of Potentiality and Actuality, ''potentiality''. Common types of potential energy include gravitational potential energy, the elastic potential energy of a deformed spring, and the electric potential energy of an electric charge and an electric field. The unit for energy in the International System of Units (SI) is the joule (symbol J). Potential energy is associated with forces that act on a body in a way that the total Work (physics), work done by these forces on the body depends only on the initial and final positions of the b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Robert and Halliday, David (1960) ''Physics'', Section 7-5, Wiley International Edition The kinetic energy of an object is equal to the work, or force ( F) in the direction of motion times its displacement ( s), needed to accelerate the object from rest to its given speed. The same amount of work is done by the object when decelerating from its current speed to a state of rest. The SI unit of energy is the joule, while the English unit of energy is the foot-pound. In relativistic mechanics, \fracmv^2 is a good approximation of kinetic energy only when ''v'' is much less than the speed of light. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', meaning "motion". The dichoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek alphabet, Greek letter (Rho (letter), rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the Electrical resistance, resistance between these contacts is , then the resistivity of the material is . Electrical conductivity (or specific conductance) is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter (Sigma (letter), sigma), but (kappa) (especially in electrical engineering) and (gamma) are sometimes used. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semimetal
A semimetal is a material with a small energy overlap between the bottom of the Electrical conduction, conduction Electronic band structure, band and the top of the valence band, but they do not overlap in momentum space. According to Band theory, electronic band theory, solids can be classified as Insulator (electricity), insulators, semiconductors, semimetals, or metals. In insulators and semiconductors the filled valence band is separated from an empty conduction band by a band gap. For insulators, the magnitude of the band gap is larger (e.g., > 4 Electronvolt, eV) than that of a semiconductor (e.g., < 4 eV). Because of the slight overlap between the conduction and valence bands, semimetals have no band gap and a small density of states at the Fermi level. A metal, by contrast, has an appreciable density of states at the Fermi level because the conduction band is partially filled. Temperature dependency The insulating/semiconducting st ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Insulator (electricity)
An electrical insulator is a material in which electric current does not flow freely. The atoms of the insulator have tightly bound electrons which cannot readily move. Other materials—semiconductors and electrical conductor, conductors—conduct electric current more easily. The property that distinguishes an insulator is its resistivity; insulators have higher resistivity than semiconductors or conductors. The most common examples are Nonmetal (chemistry), non-metals. A perfect insulator does not exist because even the materials used as insulators contain small numbers of mobile charges (charge carriers) which can carry current. In addition, all insulators become electrically conductive when a sufficiently large voltage is applied that the electric field tears electrons away from the atoms. This is known as electrical breakdown, and the voltage at which it occurs is called the breakdown voltage of an insulator. Some materials such as glass, Electrical insulation paper, paper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
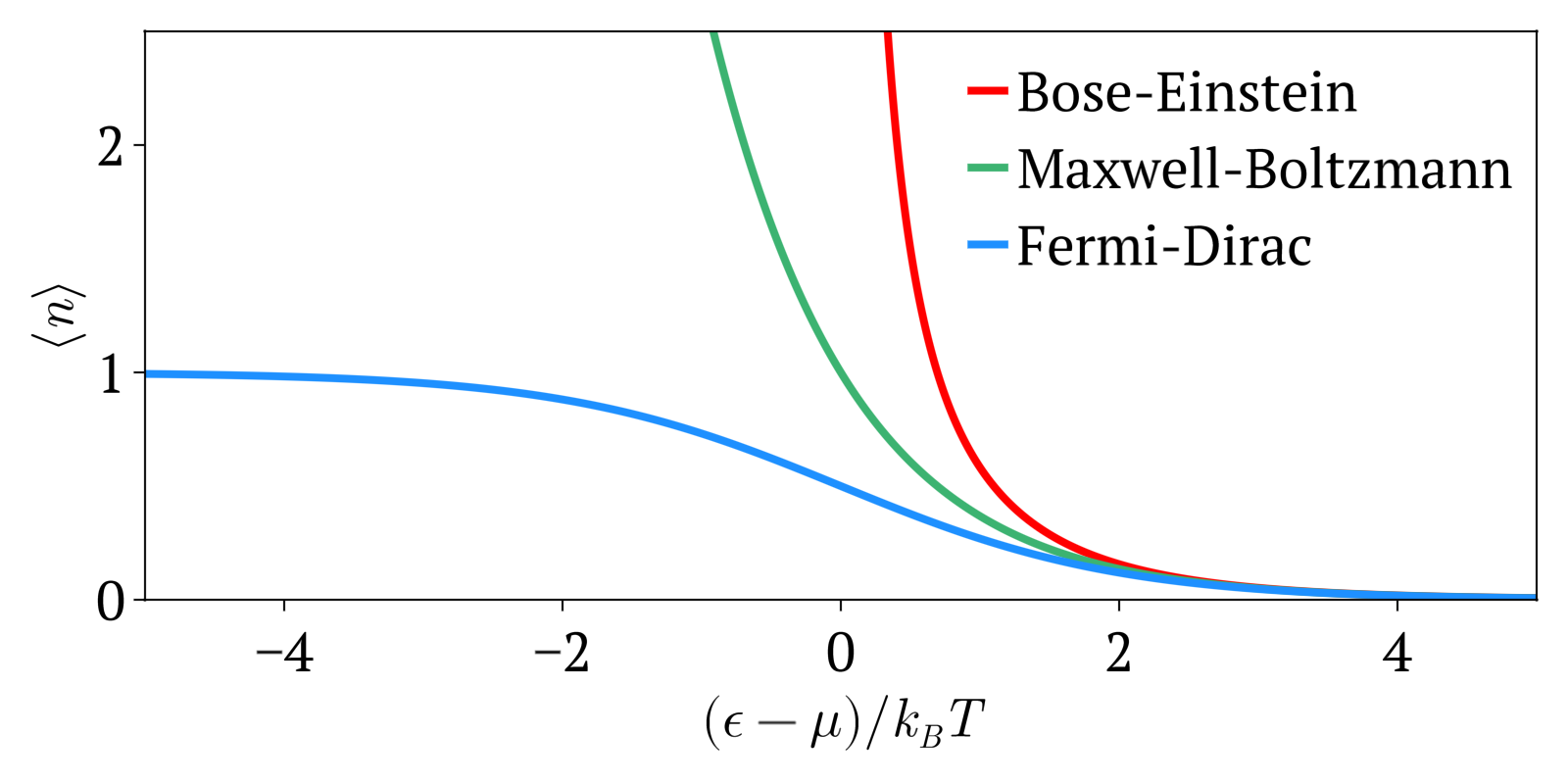
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |