|
Elongation (astronomy)
In astronomy, a planet's elongation is the angular separation between the Sun and the planet, with Earth as the vertex (geometry), reference point. The greatest elongation is the maximum angular separation. ephemeris, Astronomical tables and websites, such as Heavens-Above, forecast when and where the planets reach their next maximum elongations. Sometimes elongation may instead refer to the angular distance of the Moon relative Earth or the natural satellite of another planet from its central planet, for instance the angular distance of Io (moon), Io from Jupiter. A Quadrature (astronomy), quadrature occurs when the position of a body (moon or planet) is such that its elongation is 90° or 270°; i.e. the body-earth-sun angle is 90°. Of inferior planets The greatest elongation of a given inferior planet occurs when this planet's position, in its orbital path around the Sun, is at tangent to the observer on Earth. Since an inferior planet is well within the area of Earth's o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positional Astronomy
Positional notation, also known as place-value notation, positional numeral system, or simply place value, usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the values may be modified when combined). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sunset
Sunset (or sundown) is the disappearance of the Sun at the end of the Sun path, below the horizon of the Earth (or any other astronomical object in the Solar System) due to its Earth's rotation, rotation. As viewed from everywhere on Earth, it is a phenomenon that happens approximately once every 24 hours, except in areas close to the Geographical pole, poles. The equinox Sun sets due west at the moment of both the spring and autumn equinoxes. As viewed from the Northern Hemisphere, the Sun sets to the northwest (or not at all) in the spring and summer, and to the southwest in the autumn and winter; these seasons are reversed for the Southern Hemisphere. The sunset is defined in astronomy the moment the upper limb of the Sun disappears below the horizon. Near the horizon, atmospheric refraction causes sunlight rays to be distorted to such an extent that geometrically the solar disk is already about one diameter below the horizon when a sunset is observed. Sunset is distinct from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synodic Period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit. For celestial objects in general, the orbital period is determined by a 360° revolution of orbiting body, one body around its primary body, primary, ''e.g.'' Earth around the Sun. Periods in astronomy are expressed in units of time, usually hours, days, or years. Its reciprocal is the orbital frequency, a kind of revolution speed, revolution frequency, in units of hertz. Small body orbiting a central body According to Kepler's laws of planetary motion, Kepler's Third Law, the orbital period ''T'' of two point masses orbiting each other in a circular or elliptic orbit is: :T = 2\pi\sqrt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Velocity
In physics, angular velocity (symbol or \vec, the lowercase Greek letter omega), also known as the angular frequency vector,(UP1) is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates (spins or revolves) around an axis of rotation and how fast the axis itself changes direction. The magnitude of the pseudovector, \omega=\, \boldsymbol\, , represents the '' angular speed'' (or ''angular frequency''), the angular rate at which the object rotates (spins or revolves). The pseudovector direction \hat\boldsymbol=\boldsymbol/\omega is normal to the instantaneous plane of rotation or angular displacement. There are two types of angular velocity: * Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. * Spin angular velocity refers to how fast a rigid body rotates around a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariable Plane
The invariable plane of a planetary system, also called Laplace's invariable plane, is the plane passing through its barycenter (center of mass) perpendicular to its angular momentum vector. Solar System In the Solar System, about 98% of this effect is contributed by the orbital angular momenta of the four giant planets (Jupiter, Saturn, Uranus, and Neptune). The invariable plane is within 0.5° of the orbital plane of Jupiter, and may be regarded as the weighted average of all planetary orbital and rotational planes. Terminology and definition This plane is sometimes called the "Laplacian" or "Laplace plane" or the "invariable plane of Laplace", though it should not be confused with the Laplace plane, which is the plane about which the individual orbital planes of planetary satellites precess. Both derive from the work of (and are at least sometimes named for) the French astronomer Pierre-Simon Laplace. — English translation published in four volumes, 1829–1839; : ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecliptic
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the fixed stars, background of stars – specifically the Zodiac constellations. The planets of the Solar System can also be seen along the ecliptic, because their orbital planes are very close to Earth's. The Moon's orbital plane is also similar to Earth's; the ecliptic is so named because the ancients noted that eclipses only occur when the Moon is crossing it. The ecliptic is an important Plane of reference, reference plane and is the basis of the ecliptic coordinate system. Ancient scientists were able to calculate Earth's axial tilt by comparing the ecliptic plane to that of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference Plane
In celestial mechanics, the orbital plane of reference (or orbital reference plane) is the plane used to define orbital elements (positions). The two main orbital elements that are measured with respect to the plane of reference are the inclination and the longitude of the ascending node. Depending on the type of body being described, there are four different kinds of reference planes that are typically used: *The ecliptic or invariable plane for planets, asteroids, comets, etc. within the Solar System, as these bodies generally have orbits that lie close to the ecliptic. *The equatorial plane of the orbited body for satellites orbiting with small semi-major axes *The local Laplace plane for satellites orbiting with intermediate-to-large semi-major axes *The plane tangent to celestial sphere for extrasolar objects On the plane of reference, a zero-point must be defined from which the angles of longitude are measured. This is usually defined as the point on the celestial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Plane
The orbital plane of a revolving body is the geometric plane in which its orbit lies. Three non-collinear points in space suffice to determine an orbital plane. A common example would be the positions of the centers of a massive body (host) and of an orbiting celestial body at two different times/points of its orbit. The orbital plane is defined in relation to a reference plane by two parameters: inclination (''i'') and longitude of the ascending node (Ω). By definition, the reference plane for the Solar System is usually considered to be Earth's orbital plane, which defines the ecliptic, the circular path on the celestial sphere that the Sun appears to follow over the course of a year. In other cases, for instance a moon or artificial satellite orbiting another planet, it is convenient to define the inclination of the object's orbit as the angle between its orbital plane and the planet's equatorial plane. The coordinate system defined that uses the orbital plane as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degrees. For a satellite orbiting a planet, the plane of reference is usually the plane containing the planet's equator. For pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
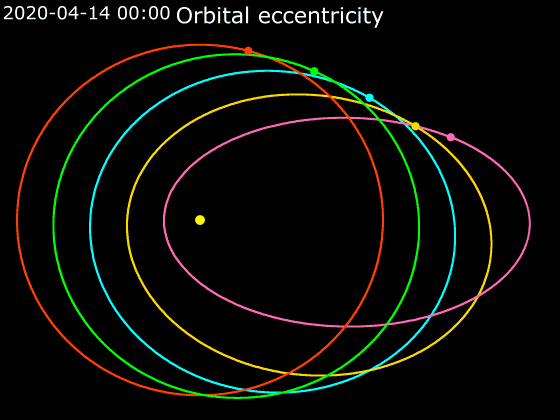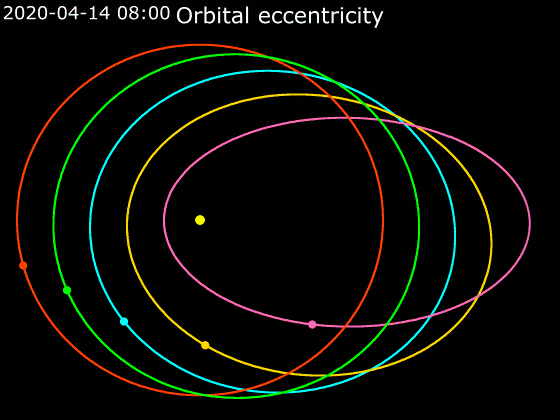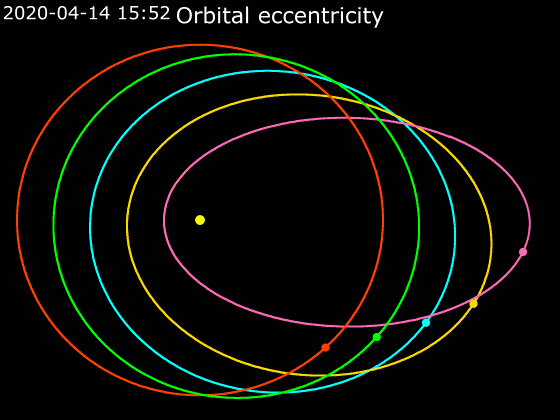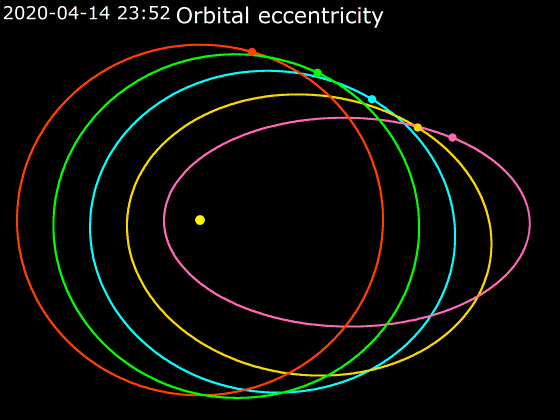
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, Potential energy, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no Radial orbit, radial version. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the Center of mass, center of the central mass perpendicular to the orbital plane. Circular acceleration :wikt:transverse, Transverse acceleration (perpendicular to velocity) causes a change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates concerning time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is Kinetic e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |