|
Elongated Gyrobifastigium
In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces. Name The first name is from the regular-faced gyrobifastigium but Elongation (geometry), elongated with 4 triangles expanded into pentagons. The name of the gyrobifastigium comes from the Latin ''fastigium'', meaning a sloping roof. In the standard naming convention of the Johnson solids, ''bi-'' means two solids connected at their bases, and ''gyro-'' means the two halves are twisted with respect to each other. The gyrobifastigium is first in a series of gyrobicupola, so this solid can also be called an ''elongated digonal gyrobicupola''. Geometrically it can also be constructed as the dual of a digonal gyrobianticupola. This construction is space-filling. The second name, ''gabled rhombohedron'', is from Michael Goldberg's paper on space-filling octahedra, model 8-VI, the 6th of at least 49 space-filling octahedra. A gable is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Triangular Prismatic Honeycomb
The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed entirely of triangular prisms. It is constructed from a triangular tiling extruded into prisms. It is one of 28 convex uniform honeycombs. It consists of 1 + 6 + 1 = 8 edges meeting at a vertex, There are 6 triangular prism cells meeting at an edge and faces are shared between 2 cells. Related honeycombs Hexagonal prismatic honeycomb The hexagonal prismatic honeycomb or hexagonal prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of hexagonal prisms. It is constructed from a hexagonal tiling extruded into prisms. It is one of 28 convex uniform honeycombs. This honeycomb can be alternated into the gyrated tetrahedral-octahedral honeycomb, with pairs of tetrahedra existing in the alternated gaps (instead of a triangular bipyramid). There are 1 + 3 + 1 = 5 edges meeting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
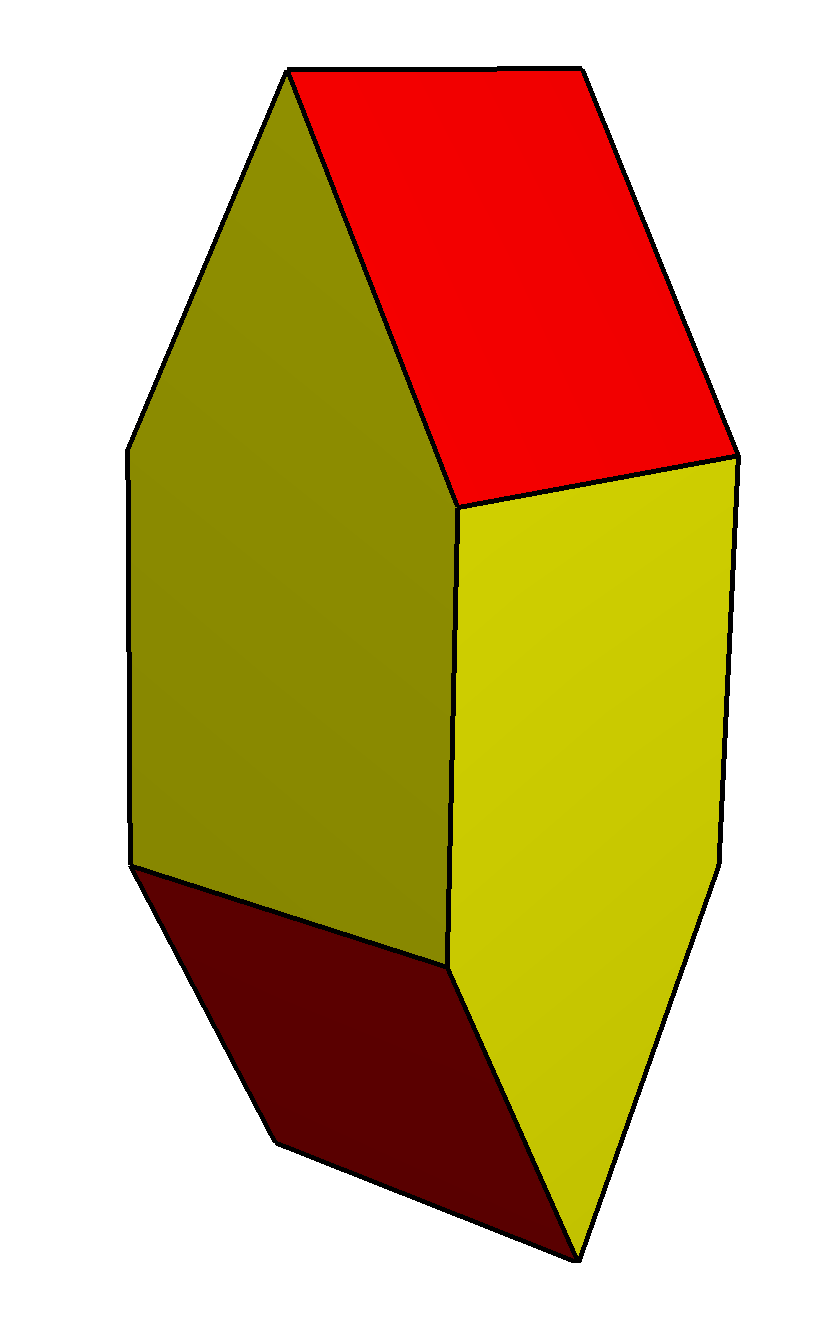
Elongated Digonal Gyrobicupola
In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces. Name The first name is from the regular-faced gyrobifastigium but elongated with 4 triangles expanded into pentagons. The name of the gyrobifastigium comes from the Latin ''fastigium'', meaning a sloping roof. In the standard naming convention of the Johnson solids, ''bi-'' means two solids connected at their bases, and ''gyro-'' means the two halves are twisted with respect to each other. The gyrobifastigium is first in a series of gyrobicupola, so this solid can also be called an ''elongated digonal gyrobicupola''. Geometrically it can also be constructed as the dual of a digonal gyrobianticupola. This construction is space-filling. The second name, ''gabled rhombohedron'', is from Michael Goldberg's paper on space-filling octahedra, model 8-VI, the 6th of at least 49 space-filling octahedra. A gable is the triangular portion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereohedron
In geometry and crystallography, a stereohedron is a convex polyhedron that isohedral tiling, fills space isohedrally, meaning that the symmetries of the tiling take any copy of the stereohedron to any other copy. Two-dimensional analogues to the stereohedra are called planigons. Higher dimensional polytopes can also be stereohedra, while they would more accurately be called stereotopes. Plesiohedra A subset of stereohedra are called plesiohedrons, defined as the Voronoi diagram, Voronoi cells of a symmetric Delone set. Parallelohedrons are plesiohedra which are space-filling by translation only. Edges here are colored as parallel vectors. Other periodic stereohedra The catoptric tessellation contain stereohedra cells. Dihedral angles are integer divisors of 180°, and are colored by their order. The first three are the fundamental domains of _3, _3, and _3 symmetry, represented by Coxeter-Dynkin diagrams: , and . _3 is a half symmetry of _3, and _3 is a quarter symmetry. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Gyrobifastigium Concave
Elongation may refer to: * Elongation (astronomy) * Elongation (geometry) * Elongation (plasma physics) * Part of transcription of DNA into RNA of all types, including mRNA, tRNA, rRNA, etc. * Part of translation (biology) of mRNA into proteins * Elongated organisms * Elongation (mechanics) In physics and continuum mechanics, deformation is the change in the shape or size of an object. It has dimension of length with SI unit of metre (m). It is quantified as the residual displacement of particles in a non- rigid body, from an con ..., linear deformation See also * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Gyrobifastigium Conplanar
Elongation may refer to: * Elongation (astronomy) * Elongation (geometry) * Elongation (plasma physics) * Part of Transcription (biology)#Elongation, transcription of DNA into RNA of all types, including mRNA, tRNA, rRNA, etc. * Part of translation (biology) of mRNA into proteins * Anatomical terms of location#Elongated organisms, Elongated organisms * Elongation (mechanics), linear deformation See also * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Digonal Gyrobicupola2
Elongation may refer to: * Elongation (astronomy) * Elongation (geometry) * Elongation (plasma physics) * Part of transcription of DNA into RNA of all types, including mRNA, tRNA, rRNA, etc. * Part of translation (biology) of mRNA into proteins * Elongated organisms * Elongation (mechanics) In physics and continuum mechanics, deformation is the change in the shape or size of an object. It has dimension of length with SI unit of metre (m). It is quantified as the residual displacement of particles in a non- rigid body, from an con ..., linear deformation See also * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissection (geometry)
In geometry, a dissection problem is the problem of partitioning a geometric figure (such as a polytope or ball) into smaller pieces that may be rearranged into a new figure of equal content. In this context, the partitioning is called simply a dissection (of one polytope into another). It is usually required that the dissection use only a finite number of pieces. Additionally, to avoid set-theoretic issues related to the Banach–Tarski paradox and Tarski's circle-squaring problem, the pieces are typically required to be well-behaved. For instance, they may be restricted to being the closures of disjoint open sets. Polygon dissection problem The Bolyai–Gerwien theorem states that any polygon may be dissected into any other polygon of the same area, using interior-disjoint polygonal pieces. It is not true, however, that any polyhedron has a dissection into any other polyhedron of the same volume using polyhedral pieces (see Dehn invariant). This process ''is'' possible, how ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Prism
In geometry, a triangular prism or trigonal prism is a Prism (geometry), prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangular prism may be both Semiregular polyhedron, semiregular and Uniform polyhedron, uniform. The triangular prism can be used in constructing another polyhedron. Examples are some of the Johnson solids, the truncated right triangular prism, and Schönhardt polyhedron. Properties A triangular prism has 6 vertices, 9 edges, and 5 faces. Every prism has 2 congruent faces known as its ''bases'', and the bases of a triangular prism are triangles. The triangle has 3 vertices, each of which pairs with another triangle's vertex, making up another 3 edges. These edges form 3 parallelograms as other faces. If the prism's edges are perpendicular to the base, the lateral faces are rectangles, and the prism is called a ''right triangular prism''. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |