|
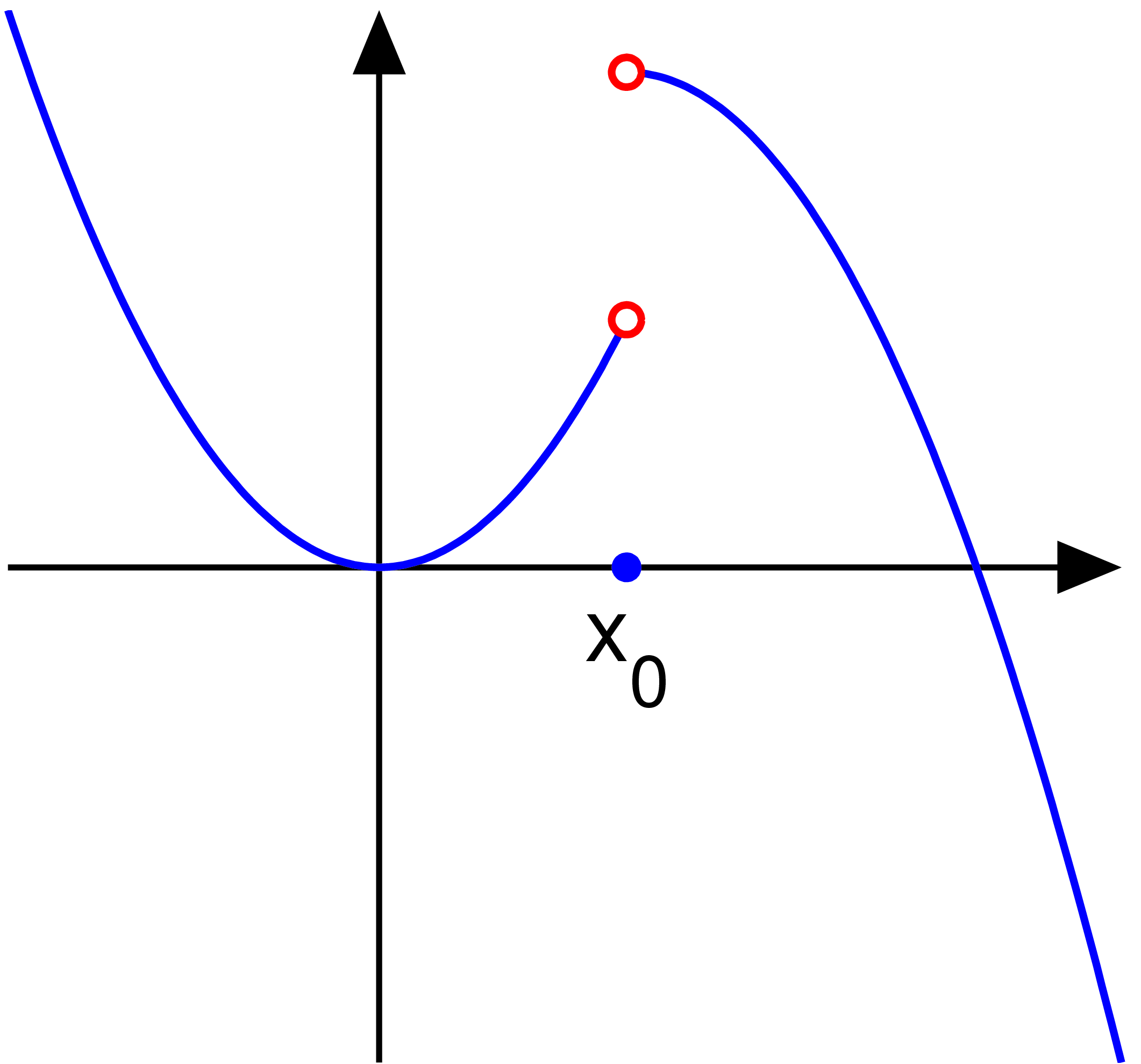
Differentiability
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Function
In mathematics, the Weierstrass function is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is an example of a fractal curve. It is named after its discoverer Karl Weierstrass. The Weierstrass function has historically served the role of a pathological function, being the first published example (1872) specifically concocted to challenge the notion that every continuous function is differentiable except on a set of isolated points. Weierstrass's demonstration that continuity did not imply almost-everywhere differentiability upended mathematics, overturning several proofs that relied on geometric intuition and vague definitions of smoothness. These types of functions were denounced by contemporaries: Henri Poincaré famously described them as "monsters" and called Weierstrass' work "an outrage against common sense", while Charles Hermite wrote that they were a "lamentable scourge". The functions were impossible to visualize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Tangent
In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. Limit definition A function ƒ has a vertical tangent at ''x'' = ''a'' if the difference quotient used to define the derivative has infinite limit: :\lim_\frac = \quad\text\quad\lim_\frac = . The first case corresponds to an upward-sloping vertical tangent, and the second case to a downward-sloping vertical tangent. The graph of ƒ has a vertical tangent at ''x'' = ''a'' if the derivative of ƒ at ''a'' is either positive or negative infinity. For a continuous function, it is often possible to detect a vertical tangent by taking the limit of the derivative. If :\lim_ f'(x) = \text then ƒ must have an upward-sloping vertical tangent at ''x'' = ''a''. Similarly, if :\lim_ f'(x) = \text then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermediate Value Theorem
In mathematical analysis, the intermediate value theorem states that if f is a continuous function whose domain contains the interval , then it takes on any given value between f(a) and f(b) at some point within the interval. This has two important corollaries: # If a continuous function has values of opposite sign inside an interval, then it has a root in that interval (Bolzano's theorem). # The image of a continuous function over an interval is itself an interval. Motivation This captures an intuitive property of continuous functions over the real numbers: given ''f'' continuous on ,2/math> with the known values f(1) = 3 and f(2) = 5, then the graph of y = f(x) must pass through the horizontal line y = 4 while x moves from 1 to 2. It represents the idea that the graph of a continuous function on a closed interval can be drawn without lifting a pencil from the paper. Theorem The intermediate value theorem states the following: Consider an interval I = ,b/math> of real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darboux's Theorem (analysis)
In mathematics, Darboux's theorem is a theorem in real analysis, named after Jean Gaston Darboux. It states that every function that results from the differentiation of another function has the intermediate value property: the image of an interval is also an interval. When ''ƒ'' is continuously differentiable (''ƒ'' in ''C''1( 'a'',''b''), this is a consequence of the intermediate value theorem. But even when ''ƒ′'' is ''not'' continuous, Darboux's theorem places a severe restriction on what it can be. Darboux's theorem Let I be a closed interval, f\colon I\to \R be a real-valued differentiable function. Then f' has the intermediate value property: If a and b are points in I with a such that f'(x)=y.Apostol, Tom M.: Mathematical Analysis: A Modern Approach to Advanced Calculus, 2nd edition, Addison-Wesley Longman, Inc. (1974), page 112.Olsen, Lars: ''A New Proof of Darboux's Theorem'', Vol. 111, No. 8 (Oct., 2004) (pp. 713–715), The American Mathematical Monthl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiation Rules
This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus. Elementary rules of differentiation Unless otherwise stated, all functions are functions of real numbers (R) that return real values; although more generally, the formulae below apply wherever they are well defined — including the case of complex numbers (C). Constant term rule For any value of c, where c \in \mathbb, if f(x) is the constant function given by f(x) = c, then \frac = 0. Proof Let c \in \mathbb and f(x) = c. By the definition of the derivative, :\begin f'(x) &= \lim_\frac \\ &= \lim_ \frac \\ &= \lim_ \frac \\ &= \lim_ 0 \\ &= 0 \end This shows that the derivative of any constant function is 0. Differentiation is linear For any functions f and g and any real numbers a and b, the derivative of the function h(x) = af(x) + bg(x) with respect to x is: h'(x) = a f'(x) + b g'(x). In Leibniz's notation this is written as: \frac = a\frac +b\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Of Discontinuities
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. This article describes the classification of discontinuities in the simplest case of functions of a single real variable taking real values. The oscillation of a function at a point quantifies these discontinuities as follows: * in a removable discontinuity, the distance that the value of the function is off by is the oscillation; * in a jump discontinuity, the size of the jump is the oscillation (assuming that the value ''at'' the point lies between these limits of the two sides); * in an essential discontinuity, oscillation measures the failure of a limit to exist; the limit is constant. A special case is if the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jump Discontinuity
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. This article describes the classification of discontinuities in the simplest case of functions of a single real variable taking real values. The oscillation of a function at a point quantifies these discontinuities as follows: * in a removable discontinuity, the distance that the value of the function is off by is the oscillation; * in a jump discontinuity, the size of the jump is the oscillation (assuming that the value ''at'' the point lies between these limits of the two sides); * in an essential discontinuity, oscillation measures the failure of a limit to exist; the limit is constant. A special case is if the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Function X^2*sin(1 Over X)
''The'' () is a grammatical article in English, denoting persons or things already mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with pronouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of pronoun '' thee'') when followed by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Of Cos With Linear Functions Without Numbers
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)