|
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent ''mixed states''. Mixed states arise in quantum mechanics in two different situations: first when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and second when one wants to describe a physical system which is entangled with another, without describing their combined state. Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information. Definition and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection Operator
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a Hilbert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Superposition
Quantum superposition is a fundamental principle of quantum mechanics. It states that, much like waves in classical physics, any two (or more) quantum states can be added together ("superposed") and the result will be another valid quantum state; and conversely, that every quantum state can be represented as a sum of two or more other distinct states. Mathematically, it refers to a property of solutions to the Schrödinger equation; since the Schrödinger equation is linear, any linear combination of solutions will also be a solution(s) . An example of a physically observable manifestation of the wave nature of quantum systems is the interference peaks from an electron beam in a double-slit experiment. The pattern is very similar to the one obtained by diffraction of classical waves. Another example is a quantum logical qubit state, as used in quantum information processing, which is a quantum superposition of the "basis states" , 0 \rangle and , 1 \rangle . Here , 0 \r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Purity (quantum Mechanics)
In quantum mechanics, and especially quantum information theory, the purity of a normalized quantum state is a scalar defined as :\gamma \, \equiv \, \mbox(\rho^2) \, where \rho \, is the density matrix of the state. The purity defines a measure on quantum states, giving information on how much a state is mixed. Mathematical properties The purity of a normalized quantum state satisfies \frac1d \leq \gamma \leq 1 \,, where d \, is the dimension of the Hilbert space upon which the state is defined. The upper bound is obtained by \mbox(\rho)=1 \,and \mbox(\rho^2)\leq \mbox(\rho) \,(see trace). If \rho \, is a projection, which defines a pure state, then the upper bound is saturated: \mbox(\rho^2)= \mbox(\rho)=1 \, (see Projections). The lower bound is obtained by the completely mixed state, represented by the matrix \frac1d I_d \,. The purity of a quantum state is conserved under unitary transformations acting on the density matrix in the form \rho \mapsto U\rho U^\dagger \,, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Idempotent
Idempotence (, ) is the property of certain operation (mathematics), operations in mathematics and computer science whereby they can be applied multiple times without changing the result beyond the initial application. The concept of idempotence arises in a number of places in abstract algebra (in particular, in the theory of projector (linear algebra), projectors and closure operators) and functional programming (in which it is connected to the property of referential transparency). The term was introduced by American mathematician Benjamin Peirce in 1870 in the context of elements of algebras that remain invariant when raised to a positive integer power, and literally means "(the quality of having) the same power", from + ''wikt:potence, potence'' (same + power). Definition An element x of a set S equipped with a binary operator \cdot is said to be ''idempotent'' under \cdot if : . The ''binary operation'' \cdot is said to be ''idempotent'' if : . Examples * In the monoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank (linear Algebra)
In linear algebra, the rank of a matrix is the dimension of the vector space generated (or spanned) by its columns. p. 48, § 1.16 This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the " nondegenerateness" of the system of linear equations and linear transformation encoded by . There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics. The rank is commonly denoted by or ; sometimes the parentheses are not written, as in .Alternative notation includes \rho (\Phi) from and . Main definitions In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see Alternative definitions for several of these. The column rank of is the dimension of the column space of , while the row rank of is the dimension of the row space of . A fundamental result in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a Hilbert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outer Product
In linear algebra, the outer product of two coordinate vector In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. An easy example may be a position such as (5, 2, 1) in a 3-dimensiona ...s is a Matrix (mathematics), matrix. If the two vectors have dimensions ''n'' and ''m'', then their outer product is an ''n'' × ''m'' matrix. More generally, given two tensors (multidimensional arrays of numbers), their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra. The outer product contrasts with: * The dot product (a special case of "inner product"), which takes a pair of coordinate vectors as input and produces a Scalar (mathematics), scalar * The Kronecker product, which takes a pair of matrices as input and produces a block matrix * Matrix multiplication, Standard mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concepts And Methods
Concepts are defined as abstract ideas. They are understood to be the fundamental building blocks of the concept behind principles, thoughts and beliefs. They play an important role in all aspects of cognition. As such, concepts are studied by several disciplines, such as linguistics, psychology, and philosophy, and these disciplines are interested in the logical and psychological structure of concepts, and how they are put together to form thoughts and sentences. The study of concepts has served as an important flagship of an emerging interdisciplinary approach called cognitive science. In contemporary philosophy, there are at least three prevailing ways to understand what a concept is: * Concepts as mental representations, where concepts are entities that exist in the mind (mental objects) * Concepts as abilities, where concepts are abilities peculiar to cognitive agents (mental states) * Concepts as Fregean senses, where concepts are abstract objects, as opposed to mental obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
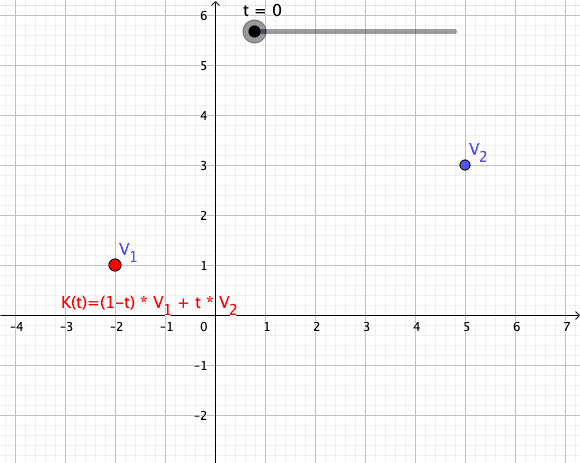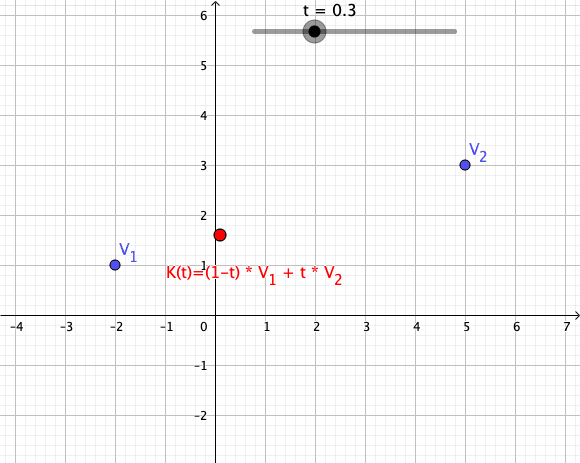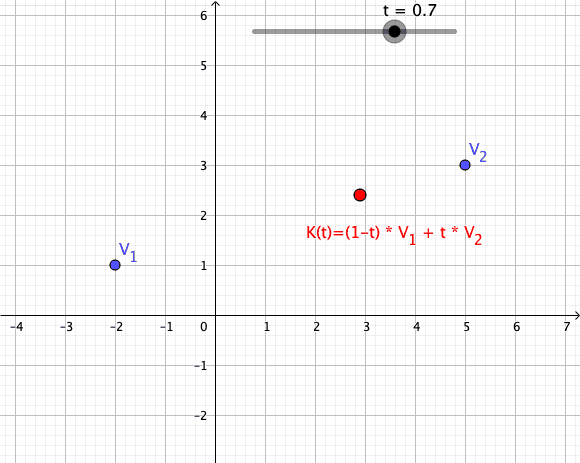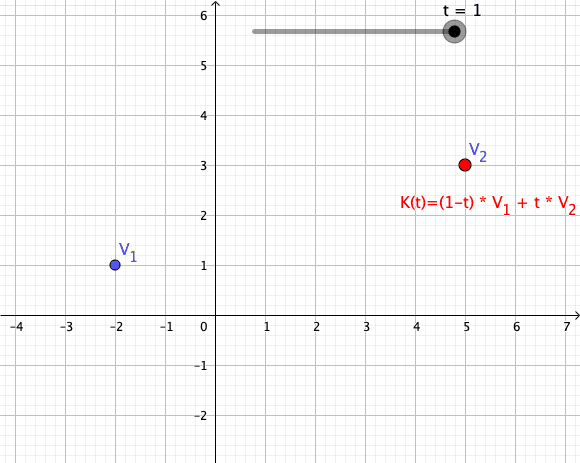
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Density Matrix
Reduction, reduced, or reduce may refer to: Science and technology Chemistry * Reduction (chemistry), part of a reduction-oxidation (redox) reaction in which atoms have their oxidation state changed. ** Organic redox reaction, a redox reaction that takes place with organic compounds ** Ore reduction: see smelting Computing and algorithms * Reduction (complexity), a transformation of one problem into another problem * Reduction (recursion theory), given sets A and B of natural numbers, is it possible to effectively convert a method for deciding membership in B into a method for deciding membership in A? * Bit Rate Reduction, an audio compression method * Data reduction, simplifying data in order to facilitate analysis * Graph reduction, an efficient version of non-strict evaluation * L-reduction, a transformation of optimization problems which keeps the approximability features * Partial order reduction, a technique for reducing the size of the state-space to be searched ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation. Details Suppose V, W are finite-dimensional vector spaces over a field, with dimensions m and n, respectively. For any space A, let L(A) denote the space of linear operators on A. The partial trace over W is then written as \operatorname_W: \operatorname(V \otimes W) \to \operatorname(V). It is defined as follows: For T\in \operatorname(V \otimes W), let e_1, \ldots, e_m , and f_1, \ldots, f_n , be bases for ''V'' and ''W'' respectively; then ''T'' has a matrix representation : \ \quad 1 \leq k, i \leq m, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)