|
Divergence Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Calculus
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, \mathbb^3. The term ''vector calculus'' is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow. Vector calculus was developed from the theory of quaternions by J. Willard Gibbs and Oliver Heaviside near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson in their 1901 book, '' Vector Analysis'', though earlier mathematicians such as Isaac Newton pioneered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are Matter, substances which cannot resist any shear force applied to them. Although the term ''fluid'' generally includes both the liquid and gas phases, its definition varies among branches of science. Definitions of ''solid'' vary as well, and depending on field, some substances can have both fluid and solid properties. Non-Newtonian fluids like Silly Putty appear to behave similar to a solid when a sudden force is applied. Substances with a very high viscosity such as Pitch (resin), pitch appear to behave like a solid (see pitch drop experiment) as well. In particle physics, the concept is extended to include fluidic matters other than liquids or gases. A fluid in medicine or biology refers to any liquid constituent of the body (body fluid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Vector
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the curve at the point. A normal vector is a vector perpendicular to a given object at a particular point. A normal vector of length one is called a unit normal vector or normal direction. A curvature vector is a normal vector whose length is the curvature of the object. Multiplying a normal vector by results in the opposite vector, which may be used for indicating sides (e.g., interior or exterior). In three-dimensional space, a surface normal, or simply normal, to a surface at point is a vector perpendicular to the tangent plane of the surface at . The vector field of normal directions to a surface is known as '' Gauss map''. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of a for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
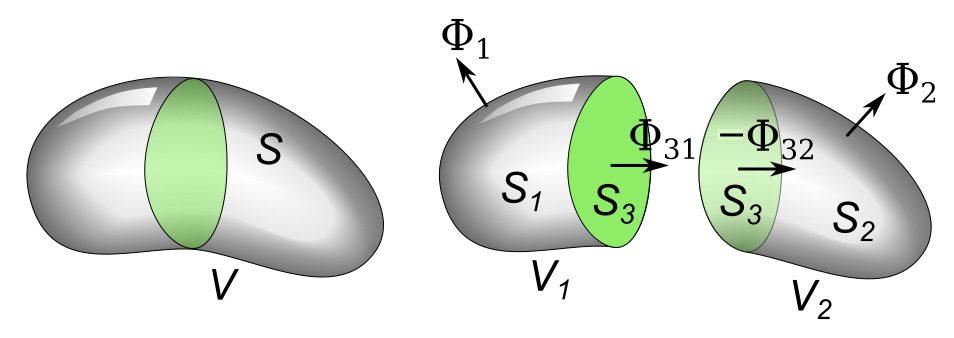
Divergence Theorem 1 - Split Volume
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to area.) More precisely, the divergence at a point is the rate that the flow of the vector field modifies a volume about the point ''in the limit'', as a small volume shrinks down to the point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal (geometry)
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the curve at the point. A normal vector is a vector perpendicular to a given object at a particular point. A normal vector of length one is called a unit normal vector or normal direction. A curvature vector is a normal vector whose length is the curvature of the object. Multiplying a normal vector by results in the opposite vector, which may be used for indicating sides (e.g., interior or exterior). In three-dimensional space, a surface normal, or simply normal, to a surface at point is a vector perpendicular to the tangent plane of the surface at . The vector field of normal directions to a surface is known as '' Gauss map''. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and Interior (topology), interior. Intuitively speaking, a neighbourhood of a point is a Set (mathematics), set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a neighbourhood of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is equivalent to the point p \in X belonging to the Interior (topology)#Interior point, topological interior of V in X. The neighbourhood V need not be an open subset of X. When V is open (resp. closed, compact, etc.) in X, it is called an (resp. closed neighbourhood, compact neighbourhood, etc.). Some authors require neighbourhoods to be open, so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Surface
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth manifold, smooth Surface (topology), surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: ''extrinsically'', relating to their embedding in Euclidean space and ''intrinsically'', reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometry, isometric embedding in Euclidean space. Surfaces naturally arise as Graph of a function, graphs of Function (mathematics), functions of a pair of Variable (mathematics), variables, and sometimes appear in parametric form or as Locus (mathematics), loci associated to Curve#Definitions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piecewise
In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be defined differently. Piecewise definition is actually a way of specifying the function, rather than a characteristic of the resulting function itself, as every function whose domain contains at least two points can be rewritten as a piecewise function. The first three paragraphs of this article only deal with this first meaning of "piecewise". Terms like piecewise linear, piecewise smooth, piecewise continuous, and others are also very common. The meaning of a function being piecewise P, for a property P is roughly that the domain of the function can be partitioned into pieces on which the property P holds, but is used slightly differently by different authors. Unlike the first meaning, this is a property of the function itself and not on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it includes all ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces. One suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called '' 3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a '' solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |