|
Discrete Modeling
Discrete modelling is the discrete analogue of continuous modelling. In discrete modelling, formulae are fit to discrete data—data that could potentially take on only a countable set of values, such as the integers, and which are not infinitely divisible. A common method in this form of modelling is to use recurrence relations. Discrete time In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "poi ... models are well-suited for step-by-step computer simulations and are often appropriate for modelling experimental data, which is typically collected in discrete form. References {{Mathapplied-stub Applied mathematics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points form a , meaning they are '' isolated'' from each other in a certain sense. The discrete topology is the finest topology that can be given on a set. Every subset is open in the discrete topology so that in particular, every singleton subset is an open set in the discrete topology. Definitions Given a set X: A metric space (E,d) is said to be '' uniformly discrete'' if there exists a ' r > 0 such that, for any x,y \in E, one has either x = y or d(x,y) > r. The topology underlying a metric space can be discrete, without the metric being uniformly discrete: for example the usual metric on the set \left\. Properties The underlying uniformity on a discrete metric space is the discrete uniformity, and the underlying topology on a discrete uniform space is the discrete topology. Thus, the different notions of discrete space are compatible with on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Continuous Modelling
Continuous modelling is the mathematical practice of applying a model A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , . Models can be divided in ... to continuous data (data which has a potentially infinite number, and divisibility, of attributes). They often use differential equations and are converse to discrete modelling. Modelling is generally broken down into several steps: * Making assumptions about the data: The modeller decides what is influencing the data and what can be safely ignored. * Making equations to fit the assumptions. * Solving the equations. * Verifying the results: Various statistical tests are applied to the data and the model and compared. * If the model passes the verification progress, putting it into practice. * If the model fails the verification progress, altering it and subje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
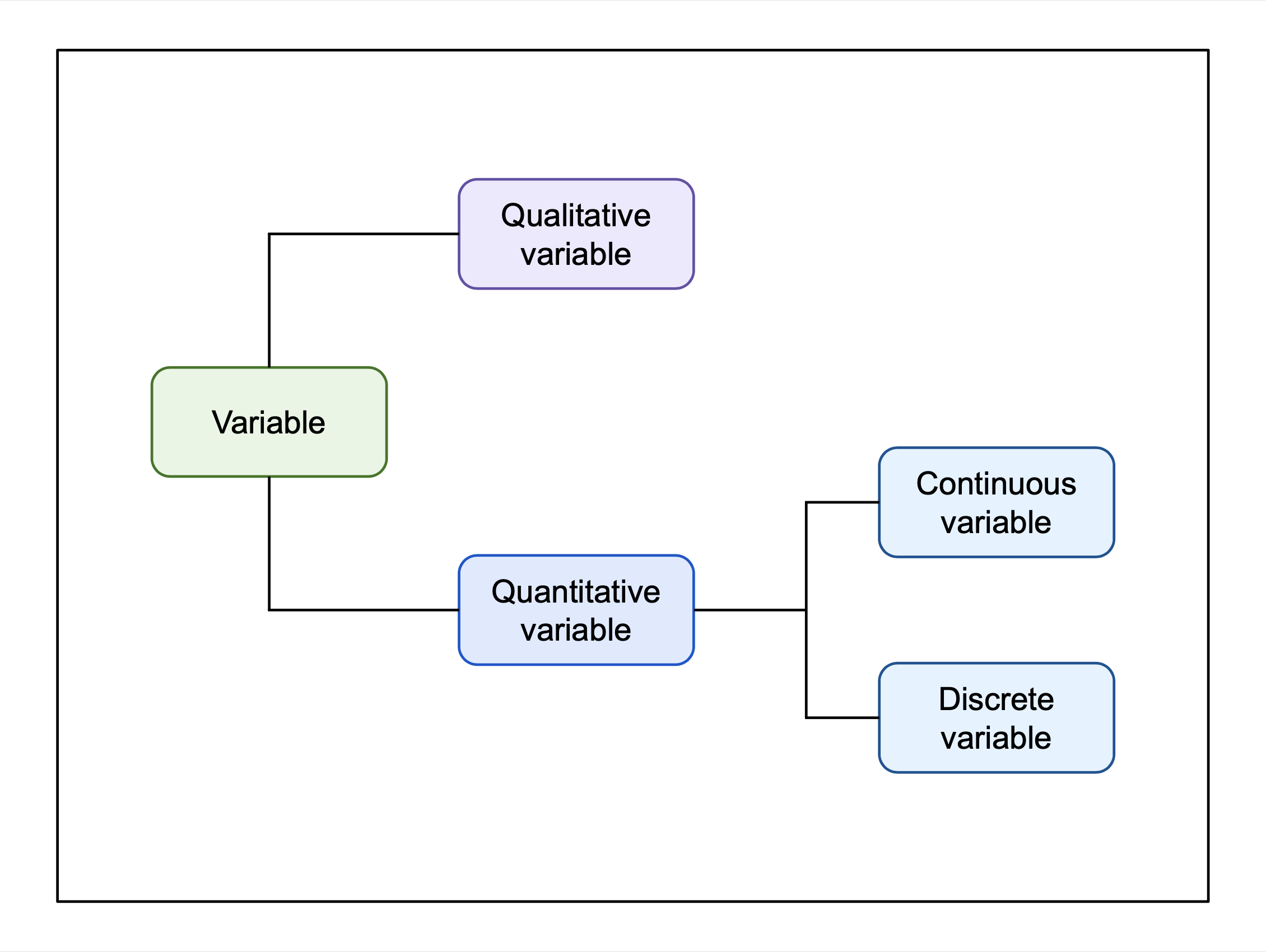
Discrete Variable
In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions. Continuous variable A continuous variable is a variable such that there are possible values between any two values. For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range. Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Data
Data ( , ) are a collection of discrete or continuous values that convey information, describing the quantity, quality, fact, statistics, other basic units of meaning, or simply sequences of symbols that may be further interpreted formally. A datum is an individual value in a collection of data. Data are usually organized into structures such as tables that provide additional context and meaning, and may themselves be used as data in larger structures. Data may be used as variables in a computational process. Data may represent abstract ideas or concrete measurements. Data are commonly used in scientific research, economics, and virtually every other form of human organizational activity. Examples of data sets include price indices (such as the consumer price index), unemployment rates, literacy rates, and census data. In this context, data represent the raw facts and figures from which useful information can be extracted. Data are collected using technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Countable
In mathematics, a Set (mathematics), set is countable if either it is finite set, finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Recurrence Relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Time And Continuous Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |