|
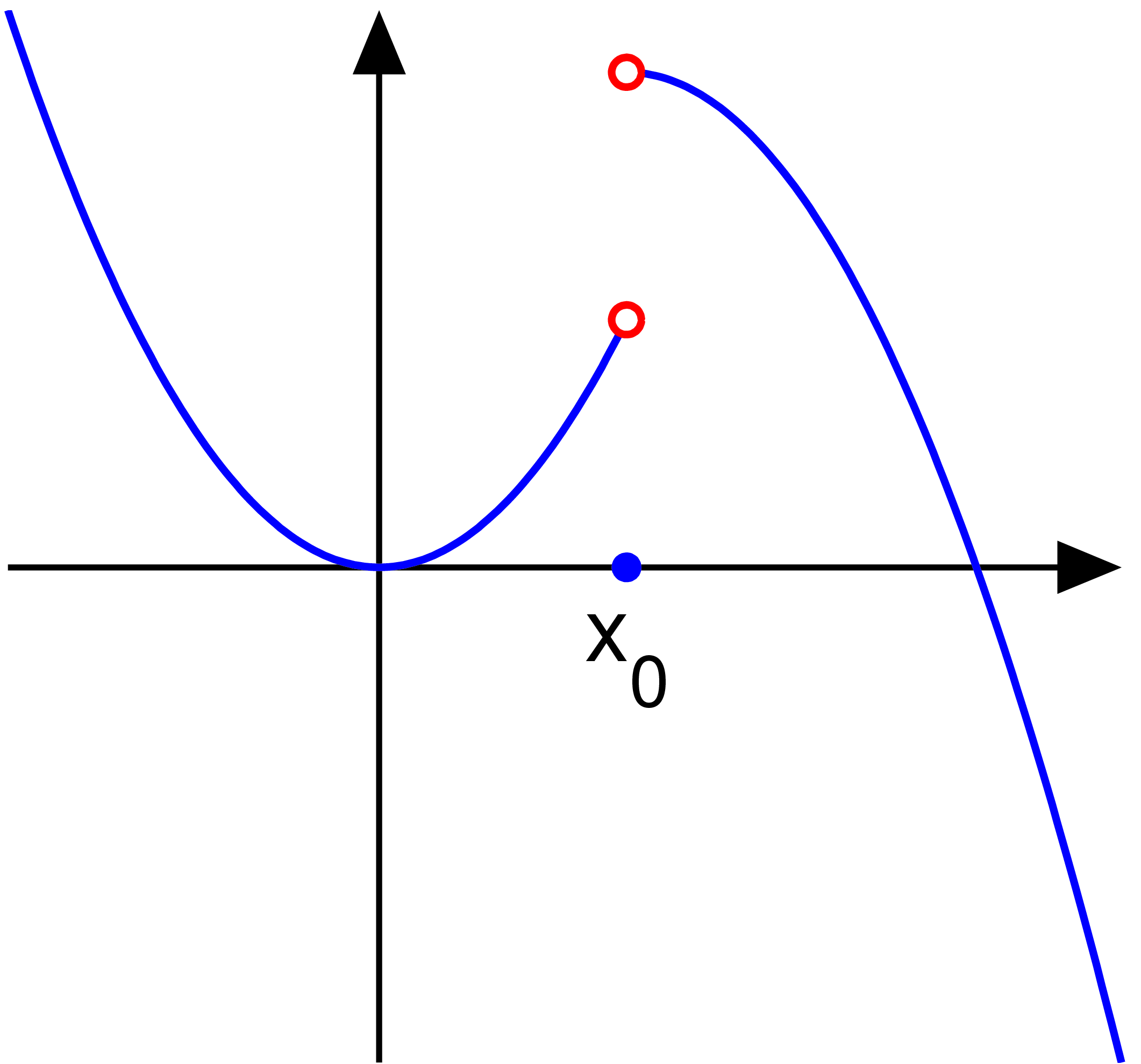
Differentiable Imaging
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary (topology)
In topology and mathematics in general, the boundary of a subset of a topological space is the set of points in the Closure (topology), closure of not belonging to the Interior (topology), interior of . An element of the boundary of is called a boundary point of . The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set include \operatorname(S), \operatorname(S), and \partial S. Some authors (for example Willard, in ''General Topology'') use the term frontier instead of boundary in an attempt to avoid confusion with a Manifold#Manifold with boundary, different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, ''Metric Spaces'' by E. T. Copson uses the term boundary to refer to Felix Hausdorff, Hausdorff's border, which is defined as the intersection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Of Discontinuities
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a limit point (also called "accumulation point" or "cluster point") of its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. The oscillation of a function at a point quantifies these discontinuities as follows: * in a removable discontinuity, the distance that the value of the function is off by is the oscillation; * in a jump discontinuity, the size of the jump is the oscillation (assuming that the value ''at'' the point lies between these limits of the two sides); * in an essential discontinuity (a.k.a. infinite discontinuity), oscillation measures the failure of a limit to exist. A special case is if the function diverges to infinity or minus infinity, in which case the oscillati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jump Discontinuity
Continuous functions are of utmost importance in mathematics, functions and applications. However, not all Function (mathematics), functions are continuous. If a function is not continuous at a limit point (also called "accumulation point" or "cluster point") of its Domain of a function, domain, one says that it has a discontinuity there. The Set theory, set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. The Oscillation (mathematics), oscillation of a function at a point quantifies these discontinuities as follows: * in a removable discontinuity, the distance that the value of the function is off by is the oscillation; * in a jump discontinuity, the size of the jump is the oscillation (assuming that the value ''at'' the point lies between these limits of the two sides); * in an essential discontinuity (a.k.a. infinite discontinuity), oscillation measures the failure of a Limit of a function, limit to exist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Function X^2*sin(1 Over X)
''The'' is a grammatical article in English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archaic pronoun ''thee' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Of Cos With Linear Functions Without Numbers
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Function
In mathematics, the Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function (mathematics), function that is continuous function, continuous everywhere but Differentiable function, differentiable nowhere. It is also an example of a fractal curve. The Weierstrass function has historically served the role of a pathological (mathematics), pathological function, being the first published example (1872) specifically concocted to challenge the notion that every continuous function is differentiable except on a set of isolated points. Weierstrass's demonstration that continuity did not imply almost-everywhere differentiability upended mathematics, overturning several proofs that relied on geometric intuition and vague definitions of smoothness. These types of functions were disliked by contemporaries: Charles Hermite, on finding that one class of function he was working on had such a property, described it as a "lamentable scourge". Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Studia Mathematica
''Studia Mathematica'' is a triannual peer-reviewed scientific journal of mathematics published by the Polish Academy of Sciences. Papers are written in English, French, German, or Russian, primarily covering functional analysis, abstract methods of mathematical analysis, and probability theory. The editor-in-chief is Adam Skalski. History The journal was established in 1929 by Stefan Banach and Hugo Steinhaus and its first editors were Banach, Steinhaus and Herman Auerbach. Due to the Second World War publication stopped after volume 9 (1940) and was not resumed until volume 10 in 1948. Abstracting and indexing The journal is abstracted and indexed in: *Current Contents/Physical, Chemical & Earth Sciences *MathSciNet *Science Citation Index *Scopus *Zentralblatt MATH According to the ''Journal Citation Reports'', the journal has a 2018 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meagre Set
In the mathematical Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ... field of general topology, a meagre set (also called a meager set or a set of first category) is a subset of a topological space that is small or Negligible set, negligible in a precise sense detailed below. A set that is not meagre is called nonmeagre, or of the second category. See below for definitions of other related terms. The meagre subsets of a fixed space form a Sigma-ideal, σ-ideal of subsets; that is, any subset of a meagre set is meagre, and the union (set theory), union of Countable set, countably many meagre sets is meagre. Meagre sets play an important role in the formulation of the notion of Baire space and of the Baire category theorem, which is used in the proof of several fundamental results ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Banach
Stefan Banach ( ; 30 March 1892 – 31 August 1945) was a Polish mathematician who is generally considered one of the 20th century's most important and influential mathematicians. He was the founder of modern functional analysis, and an original member of the Lwów School of Mathematics. His major work was the 1932 book, ''Théorie des opérations linéaires'' (Theory of Linear Operations), the first monograph on the general theory of functional analysis. Born in Kraków to a family of Gorals, Goral descent, Banach showed a keen interest in mathematics and engaged in solving mathematical problems during school Recess (break), recess. After completing his secondary education, he befriended Hugo Steinhaus, with whom he established the Polish Mathematical Society in 1919 and later published the scientific journal ''Studia Mathematica''. In 1920, he received an assistantship at the Lwów Polytechnic, subsequently becoming a professor in 1922 and a member of the Polish Academy of Lear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to the concept of measure zero, and is analogous to the notion of '' almost surely'' in probability theory. More specifically, a property holds almost everywhere if it holds for all elements in a set except a subset of measure zero, or equivalently, if the set of elements for which the property holds is conull. In cases where the measure is not complete, it is sufficient that the set be contained within a set of measure zero. When discussing sets of real numbers, the Lebesgue measure is usually assumed unless otherwise stated. The term ''almost everywhere'' is abbreviated ''a.e.''; in older literature ''p.p.'' is used, to stand for the equivalent French language phrase ''presque partout''. A set with full measure is one whose complement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Tangent
In mathematics, particularly calculus, a vertical tangent is a tangent, tangent line that is Vertical direction, vertical. Because a vertical line has Infinity, infinite slope, a Function (mathematics), function whose graph of a function, graph has a vertical tangent is not Differentiable function, differentiable at the point of tangency. Limit definition A function ƒ has a vertical tangent at ''x'' = ''a'' if the difference quotient used to define the derivative has Limit_of_a_function#Infinite_limits, infinite limit: :\lim_\frac = \quad\text\quad\lim_\frac = . The graph of ƒ has a vertical tangent at ''x'' = ''a'' if the derivative of ƒ at ''a'' is either positive or negative infinity. For a continuous function, it is often possible to detect a vertical tangent by taking the limit of the derivative. If :\lim_ f'(x) = \text then ƒ must have an upward-sloping vertical tangent at ''x'' = ''a''. Similarly, if :\lim_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |