|
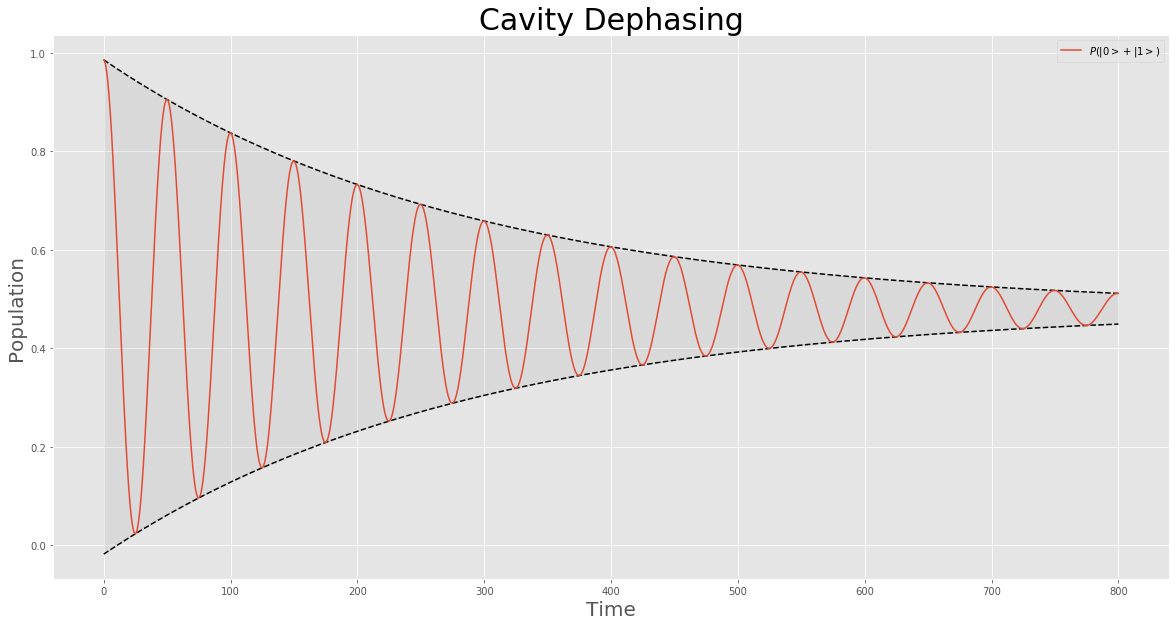
Dephasing
In physics, dephasing is a mechanism that recovers classical physics, classical behaviour from a quantum physics, quantum system. It refers to the ways in which coherence (physics), coherence caused by perturbation decays over time, and the system returns to the state before perturbation. It is an important effect in molecular and atomic spectroscopy, and in the condensed matter physics of mesoscopic devices. The reason can be understood by describing the conduction in metals as a classical phenomenon with quantum effects all embedded into an Effective mass (solid-state physics), effective mass that can be computed quantum mechanically, as also happens to Conductance quantum, resistance that can be seen as a Scattering theory, scattering effect of Valence and conduction bands, conduction electrons. When the temperature is lowered and the dimensions of the device are meaningfully reduced, this classical behaviour should disappear and the laws of quantum mechanics should govern the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dephasing Rate SP Formula
The ''SP'' formula for the dephasing rate \Gamma_ of a particle that moves in a fluctuating environment unifies various results that have been obtained, notably in condensed matter physics, with regard to the motion of electrons in a metal. The general case requires to take into account not only the temporal correlations but also the spatial correlations of the environmental fluctuations. These can be characterized by the spectral form factor \tilde(q,\omega), while the motion of the particle is characterized by its power spectrum \tilde(q,\omega). Consequently, at finite temperature the expression for the dephasing rate takes the following form that involves ''S'' and ''P'' functions: \Gamma_ \ = \ \int d \int \frac \,\tilde(,\omega) \, \tilde(-,-\omega) Due to inherent limitations of the semiclassical (stationary phase) approximation, the physically correct procedure is to use the non-symmetrized quantum versions of \tilde(q,\omega) and \tilde(q,\omega). The argument is based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
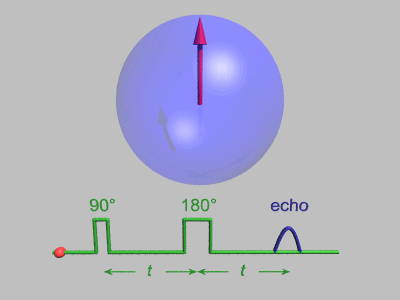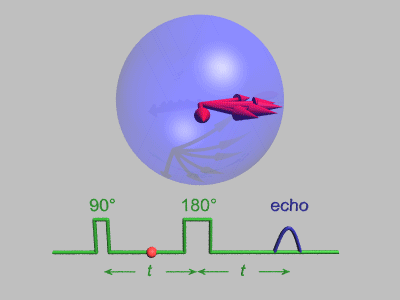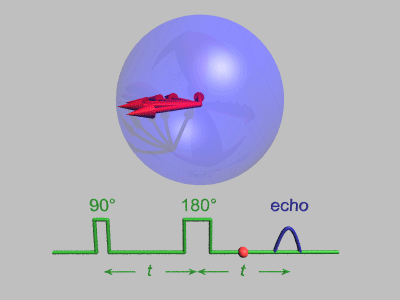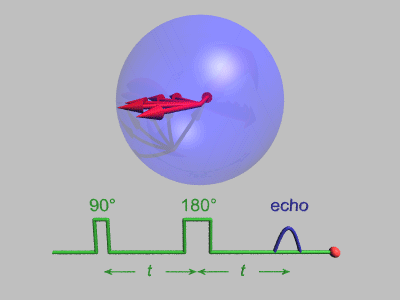
Spin Echo
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation. Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect. The NMR signal observed following an initial excitation pulse decays with time due to both spin relaxation and any ''inhomogeneous'' effects which cause spins in the sample to precess at different rates. The first of these, relaxation, leads to an irreversible loss of magnetisation. But the inhomogeneous dephasing can be removed by applying a 180° ''inversion'' pulse that inverts the magnetisation vectors. Examples of inhomogeneous effects include a magnetic field gradient and a distribution of chemical shifts. If the inversion pulse is applied after a period ''t'' of dephasing, the inhomogeneous evolution will rephase to form an echo at time 2''t''. In simple cases, the intensity of the echo relative to the initial signal is given by '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Boris Altshuler
Boris Leonidovich Altshuler (, born 27 January 1955, Leningrad, USSR) is a professor of theoretical physics at Columbia University. His specialty is theoretical condensed matter physics. Education and career Altshuler attended State Secondary School 489 in Saint Petersburg. He received his diploma in physics from Leningrad State University in 1976. Altshuler continued on at the Leningrad Institute for Nuclear Physics, where he was awarded his Ph.D. in physics in 1979. Altshuler stayed at the institute for the next ten years as a research fellow. In 1989, Altshuler joined the faculty of the Massachusetts Institute of Technology. While there, he received the Hewlett-Packard Europhysics Prize (now called the Agilent Physics Prize) and became a fellow of the American Physical Society. Altshuler left MIT in 1996 to take a professorship at Princeton University. While there, he became affiliated with NEC Laboratories America. Recently, Altshuler has joined the faculty of Columbia and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arkady Aronov
Arkady Girshevich Aronov (, ; July 26, 1939 in Leningrad, Soviet Union – November 13, 1994 in Rehovot, Israel) was a Russian and Israeli theoretical condensed matter physicist, notable for his achievements in physics of semiconductors and in mesoscopic physics. Biography Aronov was born in 1939 in Leningrad, currently Saint Petersburg, and in 1962 graduated from the Leningrad Electrotechnical Institute. He got his PhD degree from the Institute of Semiconductors of Russian Academy of Sciences in 1966 under supervision of Grigory Pikus. The title of his thesis was "Magnetic phenomena in crossed electric and magnetic fields". He stayed to work at the same institute as a researcher. In 1972, the Institute of Semiconductors was merged with into Ioffe Physical-Technical Institute. In 1974, Aronov moved to the Konstantinov Leningrad Nuclear Physics Institute, located in Gatchina. In 1977, he received there his Doktor nauk degree for the thesis "Behavior of superconductors and polari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Magnetic Field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function (mathematics), function assigning a Euclidean vector, vector to each point of space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time-resolved Spectroscopy
In physics and physical chemistry, time-resolved spectroscopy is the study of dynamic processes in materials or chemical compounds by means of spectroscopic techniques. Most often, processes are studied after the illumination of a material occurs, but in principle, the technique can be applied to any process that leads to a change in properties of a material. With the help of pulsed lasers, it is possible to study processes that occur on time scales as short as 10−16 seconds. This is done to overcome the hampering background interference that often disrupts and challenges Raman measurements to improve spectra quality. All time-resolved spectra are suitable to be analyzed using the two-dimensional correlation method for a correlation map between the peaks. Time-gated Raman spectroscopy The most common issue in conventional (CW) Raman spectroscopy (RS) is sample-induced fluorescence emission making the identification or quantification of materials challenging or impossible. An eff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spin–lattice Relaxation
During nuclear magnetic resonance observations, spin–lattice relaxation is the mechanism by which the longitudinal component of the total nuclear magnetic moment vector (parallel to the constant magnetic field) exponentially relaxes from a higher energy, non-equilibrium state to thermodynamic equilibrium with its surroundings (the "lattice"). It is characterized by the spin–lattice relaxation time, a time constant known as ''T1''. There is a different parameter, ''T2'', the spin–spin relaxation time, which concerns the exponential relaxation of the transverse component of the nuclear magnetization vector ( to the external magnetic field). Measuring the variation of ''T1'' and ''T2'' in different materials is the basis for some magnetic resonance imaging techniques. Nuclear physics ''T1'' relaxation or longitudinal relaxation curve ''T1'' characterizes the rate at which the longitudinal ''Mz'' component of the magnetization vector recovers exponentially towards its thermody ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time Constant
In physics and engineering, the time constant, usually denoted by the Greek language, Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, LTI system theory, linear time-invariant (LTI) system.Concretely, a first-order LTI system is a system that can be modeled by a single Ordinary differential equation, first order differential equation in time. Examples include the simplest single-stage electrical RC circuit#Series circuit, RC circuits and RL circuit#Series circuit, RL circuits. The time constant is the main characteristic unit of a first-order LTI system. It gives speed of the response. In the time domain, the usual choice to explore the time response is through the step response to a Heaviside step function, step input, or the impulse response to a Dirac delta function input. In the frequency domain (for example, looking at the Fourier transform of the step response, or using an input that is a simple sinusoidal function of time) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Absorption Spectrum
Absorption spectroscopy is spectroscopy that involves techniques that measure the absorption of electromagnetic radiation, as a function of frequency or wavelength, due to its interaction with a sample. The sample absorbs energy, i.e., photons, from the radiating field. The intensity of the absorption varies as a function of frequency, and this variation is the absorption spectrum. Absorption spectroscopy is performed across the electromagnetic spectrum. Absorption spectroscopy is employed as an analytical chemistry tool to determine the presence of a particular substance in a sample and, in many cases, to quantify the amount of the substance present. Infrared and ultraviolet–visible spectroscopy are particularly common in analytical applications. Absorption spectroscopy is also employed in studies of molecular and atomic physics, astronomical spectroscopy and remote sensing. There is a wide range of experimental approaches for measuring absorption spectra. The most common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Excited State
In quantum mechanics Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ..., an excited state of a system (such as an atom, molecule or Atomic nucleus, nucleus) is any quantum state of the system that has a higher energy than the ground state (that is, more energy than the absolute minimum). Excitation refers to an increase in energy level above a chosen starting point, usually the ground state, but sometimes an already excited state. The temperature of a group of particles is indicative of the level of excitation (with the notable exception of systems that exhibit negative temperature). The lifetime of a system in an excited state is usually short: Spontaneous emission, spontaneous or stimulated emission, induced emission of a quantum of energy (such as a photon or a phonon) usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |