|
Conjugate Variables
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation—in physics Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ... called the Heisenberg uncertainty principle—between them. In mathematical terms, conjugate variables are part of a symplectic basis, and the uncertainty relation corresponds to the symplectic form. Also, conjugate variables are related by Noether's theorem, which states that if the laws of physics are invariant with respect to a change in one of the conjugate variables, then the other conjugate variable will not change with time (i.e. it will be conserved). Conjugate variab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
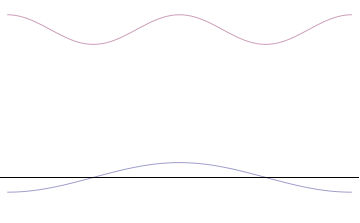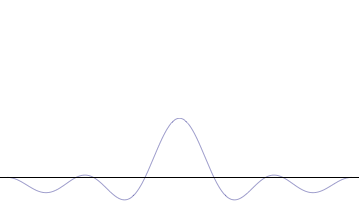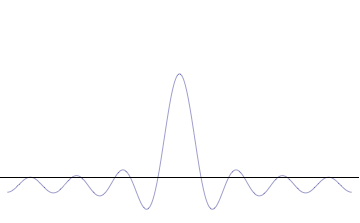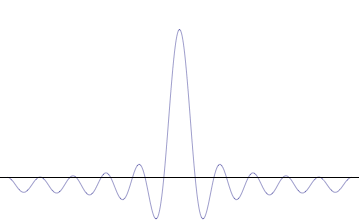
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Uncertainty Principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known. More formally, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the product of the accuracy of certain related pairs of measurements on a quantum system, such as position, ''x'', and momentum, ''p''. Such paired-variables are known as complementary variables or canonically conjugate variables. First introduced in 1927 by German physicist Werner Heisenberg, the formal inequality relating the standard deviation of position ''σx'' and the standard deviation of momentum ''σp'' was derived by Earle Hesse Kennard later that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Quantum LC Circuit
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency: :\omega = \sqrt where L is the inductance in henries, and C is the capacitance in farads. The angular frequency \omega\, has units of radians per second. A capacitor stores energy in the electric field between the plates, which can be written as follows: :U_C=\frac C V^2 =\frac Where Q is the net charge on the capacitor, calculated as : Q(t) = \int_^t I(\tau) d\tau Likewise, an inductor stores energy in the magnetic field depending on the current, which can be written as follows: :U_L=\frac L I^2 =\frac Where \phi is the branch flux, defined as :\phi(t) \equiv \int_^t V(\tau) d\tau Since charge and flux are canonically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Electric Charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and unlike charges attract each other. An object with no net charge is referred to as neutral particle, electrically neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum mechanics, quantum effects. In an isolated system, the total charge stays the same - the amount of positive charge minus the amount of negative charge does not change over time. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the atomic nucleus, nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Voltage
Voltage, also known as (electrical) potential difference, electric pressure, or electric tension, is the difference in electric potential between two points. In a Electrostatics, static electric field, it corresponds to the Work (electrical), work needed per unit of Electric charge, charge to move a positive Test particle#Electrostatics, test charge from the first point to the second point. In the SI unit, International System of Units (SI), the SI derived unit, derived unit for voltage is the ''volt'' (''V''). The voltage between points can be caused by the build-up of electric charge (e.g., a capacitor), and from an electromotive force (e.g., electromagnetic induction in a Electric generator, generator). On a macroscopic scale, a potential difference can be caused by electrochemical processes (e.g., cells and batteries), the pressure-induced piezoelectric effect, and the thermoelectric effect. Since it is the difference in electric potential, it is a physical Scalar (physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Electric Potential
Electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as electric potential energy per unit of electric charge. More precisely, electric potential is the amount of work (physics), work needed to move a test charge from a reference point to a specific point in a static electric field. The test charge used is small enough that disturbance to the field is unnoticeable, and its motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is Earth (electricity), earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar (physics), scalar quantity denoted by or occasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Rapidity
In special relativity, the classical concept of velocity is converted to rapidity to accommodate the limit determined by the speed of light. Velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are almost exactly proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates. Using the inverse hyperbolic function , the rapidity corresponding to velocity is where is the speed of light. For low speeds, by the small-angle approximation, is approximately . Since in relativity any velocity is constrained to the interval the ratio satisfies . The inverse hyperbolic tangent has the unit interval for its domain and the whole real line for its image; that is, the interval maps ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Relativistic Angular Momentum
In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics. Angular momentum is an important dynamical quantity derived from position and momentum. It is a measure of an object's rotational motion and resistance to changes in its rotation. Also, in the same way momentum conservation corresponds to translational symmetry, angular momentum conservation corresponds to rotational symmetry – the connection between symmetries and conservation laws is made by Noether's theorem. While these concepts were originally discovered in classical mechanics, they are also true and significant in special and general relativity. In terms of abstract algebra, the invariance of angular momentum, four-momentum, and other symmetries in spacetime, are described by the Lore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Orientation (geometry)
In geometry, the orientation, attitude, bearing, direction, or angular position of an object – such as a Line (geometry), line, plane (geometry), plane or rigid body – is part of the description of how it is placed in the Euclidean space, space it occupies. More specifically, it refers to the imaginary rotation that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement, in which case it may be necessary to add an imaginary translation (geometry), translation to change the object's position (geometry), position (or linear position). The position and orientation together fully describe how the object is placed in space. The above-mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its position does not change when it rotates. Euler's rotation theorem shows that in three dimensions any orien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Angular Momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction (geometry), direction and a magnitude, and both are conserved. Bicycle and motorcycle dynamics, Bicycles and motorcycles, flying discs, Rifling, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Position (vector)
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Linear Momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum (from Latin '' pellere'' "push, drive") is: \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is dimensionally equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame of reference, it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total momentum does not change. Momentum is also conserved in special relativity (with a modifi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |