|
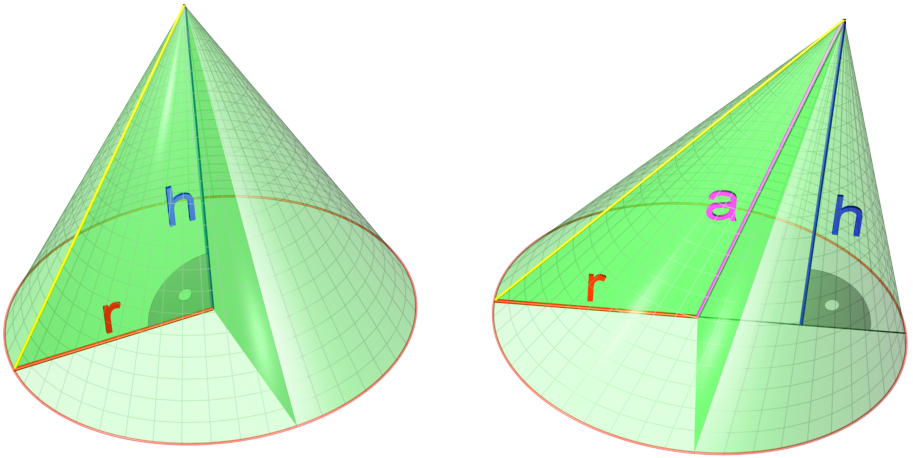
Cone Chart
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by Function composition, composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrix, orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose invertible matrix, inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact group, compact. The orthogonal group in dimension has two connected component (topology), connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unbounded Set
In mathematical analysis and related areas of mathematics, a set is called bounded if all of its points are within a certain distance of each other. Conversely, a set which is not bounded is called unbounded. The word "bounded" makes no sense in a general topological space without a corresponding metric. '' Boundary'' is a distinct concept; for example, a circle (not to be confused with a disk) in isolation is a boundaryless bounded set, while the half plane is unbounded yet has a boundary. A bounded set is not necessarily a closed set and vice versa. For example, a subset of a 2-dimensional real space constrained by two parabolic curves and defined in a Cartesian coordinate system is closed by the curves but not bounded (so unbounded). Definition in the real numbers A set of real numbers is called ''bounded from above'' if there exists some real number (not necessarily in ) such that for all in . The number is called an upper bound of . The terms ''bounded from bel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dandelin Spheres
In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.Taylor, Charles. ''An Introduction to the Ancient and Modern Geometry of Conics''page 196 ("focal spheres") (Deighton, Bell and co., 1881). The Dandelin spheres were discovered in 1822. They are named in honor of the French mathematician [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directrix (conic Section)
A conic section, conic or a quadratic curve is a curve obtained from a Conical surface, cone's surface intersecting a plane (mathematics), plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The Greek mathematics, ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set (mathematics), set of those points whose distances to some particular point, called a ''Focus (geometry), focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''Eccentricity (mathematics), eccentricity''. The type of conic is determined by the value of the ec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Cone
A projective cone (or just cone) in projective geometry is the union of all lines that intersect a projective subspace ''R'' (the apex of the cone) and an arbitrary subset ''A'' (the basis) of some other subspace ''S'', disjoint from ''R''. In the special case that ''R'' is a single point, ''S'' is a plane, and ''A'' is a conic section on ''S'', the projective cone is a conical surface; hence the name. Definition Let ''X'' be a projective space over some field ''K'', and ''R'', ''S'' be disjoint subspaces of ''X''. Let ''A'' be an arbitrary subset of ''S''. Then we define ''RA'', the cone with top ''R'' and basis ''A'', as follows : * When ''A'' is empty, ''RA'' = ''A''. * When ''A'' is not empty, ''RA'' consists of all those points on a line connecting a point on ''R'' and a point on ''A''. Properties * As ''R'' and ''S'' are disjoint, one may deduce from linear algebra and the definition of a projective space that every point on ''RA'' not in ''R'' or ''A'' is on exactly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Cone
In linear algebra, a cone—sometimes called a linear cone to distinguish it from other sorts of cones—is a subset of a real vector space that is closed under positive scalar multiplication; that is, C is a cone if x\in C implies sx\in C for every . This is a broad generalization of the standard cone in Euclidean space. A convex cone is a cone that is also closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. The definition of a convex cone makes sense in a vector space over any ordered field, although the field of real numbers is used most often. Definition A subset C of a vector space is a cone if x\in C implies sx\in C for every s>0. Here s>0 refers to (strict) positivity in the scalar field. Competing definitions Some other authors require ,\infty)C\subset C or even 0\in C. Some require a cone to be convex and/or satisfy C\cap-C\subset\. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area (geometry)
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while ''surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area of a square ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytopes
''Convex Polytopes'' is a graduate-level mathematics textbook about convex polytopes, higher-dimensional generalizations of three-dimensional polyhedron, convex polyhedra. It was written by Branko Grünbaum, with contributions from Victor Klee, Micha Perles, and Geoffrey Colin Shephard, G. C. Shephard, and published in 1967 by John Wiley & Sons. It went out of print in 1970. A second edition, prepared with the assistance of Volker Kaibel, Victor Klee, and Günter M. Ziegler, was published by Springer-Verlag in 2003, as volume 221 of their book series Graduate Texts in Mathematics. ''Convex Polytopes'' was the winner of the 2005 Leroy P. Steele Prize for mathematical exposition, given by the American Mathematical Society. The Basic Library List Committee of the Mathematical Association of America has recommended its inclusion in undergraduate mathematics libraries. Topics The book has 19 chapters. After two chapters introducing background material in linear algebra, topology, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |