|
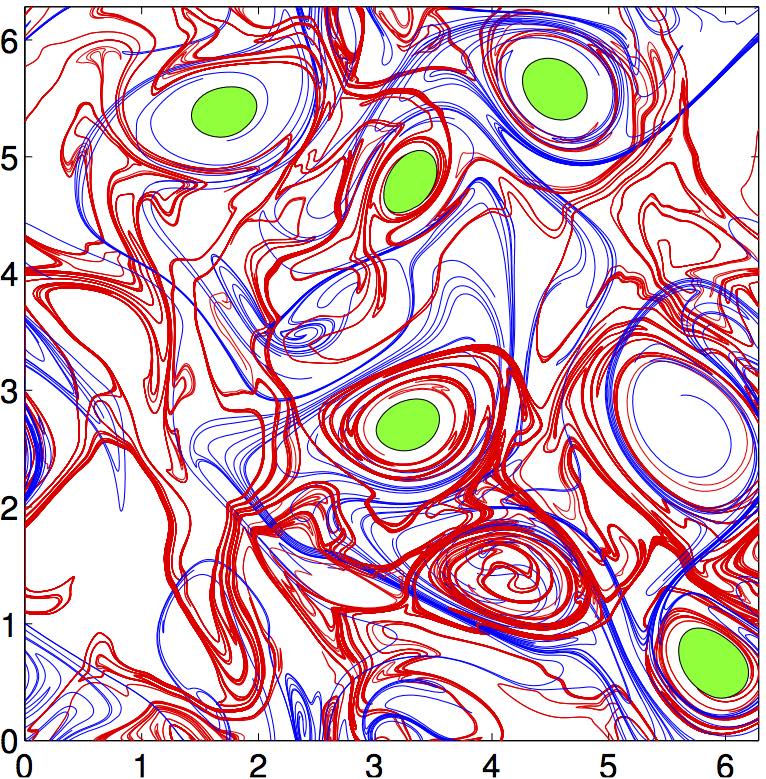
Coherent Structure
Turbulent flows are complex multi-scale and chaotic motions that need to be classified into more elementary components, referred to coherent turbulent structures. Such a structure must have temporal coherence, i.e. it must persist in its form for long enough periods that the methods of time-averaged statistics can be applied. Coherent structures are typically studied on very large scales, but can be broken down into more elementary structures with coherent properties of their own, such examples include hairpin vortices. Hairpins and coherent structures have been studied and noticed in data since the 1930s, and have been since cited in thousands of scientific papers and reviews. Flow visualization experiments, using smoke and dye as tracers, have been historically used to simulate coherent structures and verify theories, but computer models are now the dominant tools widely used in the field to verify and understand the formation, evolution, and other properties of such structures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turbulent Flow
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by Chaos theory, chaotic changes in pressure and flow velocity. It is in contrast to laminar flow, which occurs when a fluid flows in parallel layers with no disruption between those layers. Turbulence is commonly observed in everyday phenomena such as Breaking wave, surf, fast flowing rivers, billowing storm clouds, or smoke from a chimney, and most fluid flows occurring in nature or created in engineering applications are turbulent. Turbulence is caused by excessive kinetic energy in parts of a fluid flow, which overcomes the damping effect of the fluid's viscosity. For this reason, turbulence is commonly realized in low viscosity fluids. In general terms, in turbulent flow, unsteady vortices appear of many sizes which interact with each other, consequently Drag (physics), drag due to friction effects increases. The onset of turbulence can be predicted by the dimensionless Reynolds number, the rati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Stress
In fluid dynamics, the Reynolds stress is the component of the total stress tensor in a fluid obtained from the averaging operation over the Navier–Stokes equations to account for turbulent fluctuations in fluid momentum. Definition The velocity field of a flow can be split into a mean part and a fluctuating part using Reynolds decomposition. We write :u_i = \overline + u_',\, with \mathbf(\mathbf,t) being the flow velocity vector having components u_i in the x_i coordinate direction (with x_i denoting the components of the coordinate vector \mathbf). The mean velocities \overline are determined by either time averaging, spatial averaging or ensemble averaging, depending on the flow under study. Further u'_i denotes the fluctuating (turbulence) part of the velocity. We consider a homogeneous fluid, whose density ''ρ'' is taken to be a constant. For such a fluid, the components ''τ''ij'' of the Reynolds stress tensor are defined as: :\tau'_ \equiv \rho\,\overline,\, Anot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aerodynamics
Aerodynamics () is the study of the motion of atmosphere of Earth, air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an important domain of study in aeronautics. The term ''aerodynamics'' is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving Aircraft#Heavier-than-air – aerodynes, heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891. Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Numerical Simulation
A direct numerical simulation (DNS)https://eprints.soton.ac.uk/66182/1/A_primer_on_DNS.pdf "A Primer on Direct Numerical Simulation of Turbulence – Methods, Procedures and Guidelines", Coleman and Sandberg, 2010 is a simulation in computational fluid dynamics (CFD) in which the Navier–Stokes equations are numerically solved without any turbulence model. This means that the whole range of spatial and temporal scales of the turbulence must be resolved. All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales ( Kolmogorov microscales), up to the integral scale L, associated with the motions containing most of the kinetic energy. The Kolmogorov scale, \eta, is given by :\eta=(\nu^/\varepsilon)^ where \nu is the kinematic viscosity and \varepsilon is the rate of kinetic energy dissipation. On the other hand, the integral scale depends usually on the spatial scale of the boundary conditions. To satisfy these reso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Coherent Structure
Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest. As illustrated on the right, individual tracer trajectories forming coherent patterns are generally sensitive with respect to changes in their initial conditions and the system parameters. In contrast, the LCSs creating these trajectory patterns turn out to be robust and provide a simplified skeleton of the overall dynamics of the system. The robustness of this skeleton makes LCSs ideal tools for model validation, model comparison and benchmarking. LCSs can also be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Equations (fluid Dynamics)
In fluid dynamics, the Euler equations are a set of partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity. The Euler equations can be applied to incompressible and compressible flows. The incompressible Euler equations consist of Cauchy equations for conservation of mass and balance of momentum, together with the incompressibility condition that the flow velocity is divergence-free. The compressible Euler equations consist of equations for conservation of mass, balance of momentum, and balance of energy, together with a suitable constitutive equation for the specific energy density of the fluid. Historically, only the equations of conservation of mass and balance of momentum were derived by Euler. However, fluid dynamics literature often refers to the full set of the compressible Euler equations – including th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skeleton Turbulence
A skeleton is the structural frame that supports the body of most animals. There are several types of skeletons, including the exoskeleton, which is a rigid outer shell that holds up an organism's shape; the endoskeleton, a rigid internal frame to which the organs and soft tissues attach; and the hydroskeleton, a flexible internal structure supported by the hydrostatic pressure of body fluids. Vertebrates are animals with an endoskeleton centered around an axial vertebral column, and their skeletons are typically composed of bones and cartilages. Invertebrates are other animals that lack a vertebral column, and their skeletons vary, including hard-shelled exoskeleton (arthropods and most molluscs), plated internal shells (e.g. cuttlebones in some cephalopods) or rods (e.g. ossicles in echinoderms), hydrostatically supported body cavities (most), and spicules (sponges). Cartilage is a rigid connective tissue that is found in the skeletal systems of vertebrates and invertebrates. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laminar Flow
Laminar flow () is the property of fluid particles in fluid dynamics to follow smooth paths in layers, with each layer moving smoothly past the adjacent layers with little or no mixing. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another smoothly. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In laminar flow, the motion of the particles of the fluid is very orderly with particles close to a solid surface moving in straight lines parallel to that surface. Laminar flow is a flow regime characterized by high momentum diffusion and low momentum convection. When a fluid is flowing through a closed channel such as a pipe or between two flat plates, either of two types of flow may occur depending on the velocity and viscosity of the fluid: laminar flow or turbulent flow. Laminar flow occurs at lower velocities, below a threshold at which the flow becomes turbulent. The threshol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kelvin–Helmholtz Instability
The Kelvin–Helmholtz instability (after Lord Kelvin and Hermann von Helmholtz) is a fluid instability that occurs when there is shear velocity, velocity shear in a single continuum mechanics, continuous fluid or a velocity difference across the interface between two fluids. Kelvin-Helmholtz instabilities are visible in the atmospheres of planets and moons, such as in List of cloud types, cloud formations on Earth or the Great Red Spot#Great Red Spot, Red Spot on Jupiter, and the Stellar atmosphere, atmospheres of the Sun and other stars. Theory overview and mathematical concepts Fluid dynamics predicts the onset of instability and transition to turbulent flow within fluids of different density, densities moving at different speeds. If surface tension is ignored, two fluids in parallel motion with different velocities and densities yield an interface that is unstable to short-wavelength perturbations for all speeds. However, surface tension is able to stabilize the short w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eddy (fluid Dynamics)
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current (water), current created when the fluid is in a Turbulence, turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid behind the obstacle flows into the void creating a swirl of fluid on each edge of the obstacle, followed by a short reverse flow of fluid behind the obstacle flowing upstream, toward the back of the obstacle. This phenomenon is naturally observed behind large emergent rocks in swift-flowing rivers. An eddy is a movement of fluid that deviates from the general flow of the fluid. An example for an eddy is a vortex which produces such deviation. However, there are other types of eddies that are not simple vortices. For example, a Rossby wave is an eddy which is an undulation that is a deviation from mean flow, but does not have the local closed streamlines of a vortex. Swirl and eddies in engineering The propensi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |