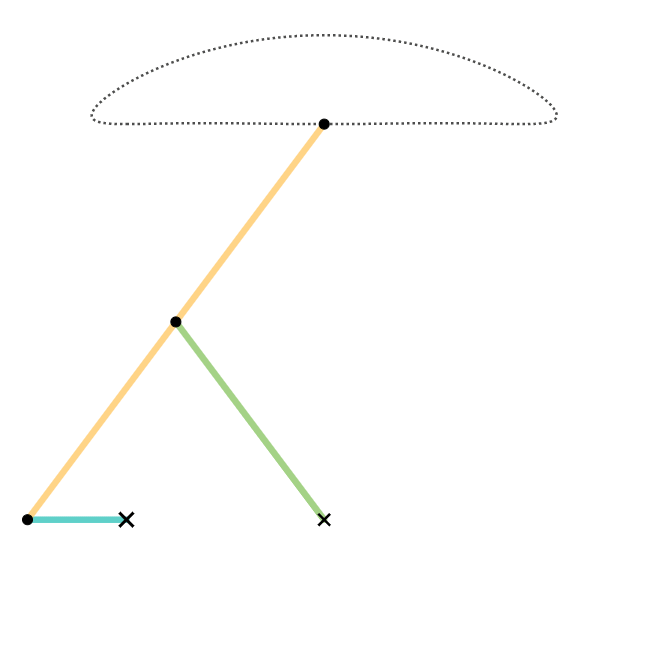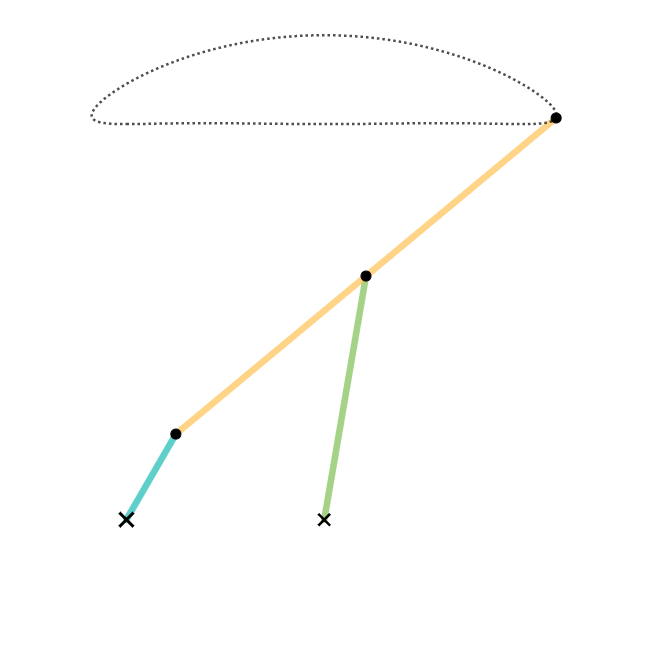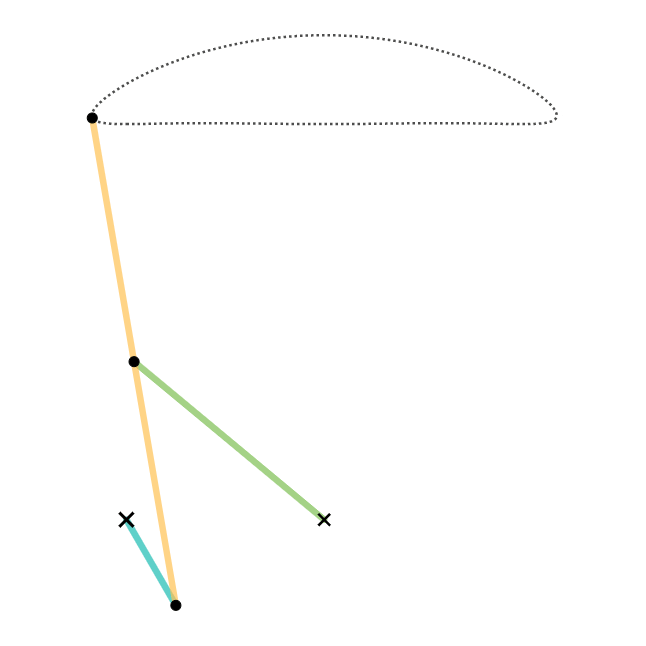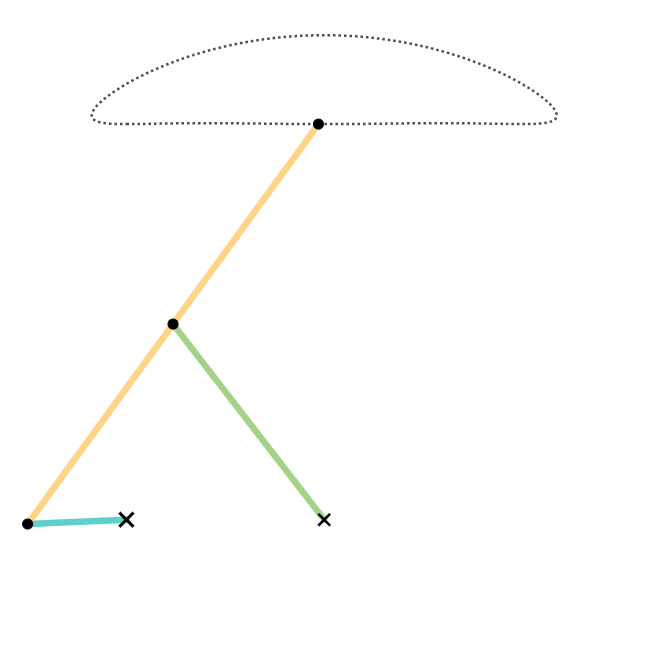|
Cognate Linkage
In kinematics, cognate linkages are linkages that ensure the same coupler curve geometry or input-output relationship, while being dimensionally dissimilar. In case of four-bar linkage coupler cognates, the Roberts–Chebyshev Theorem, after Samuel Roberts and Pafnuty Chebyshev, Retrieved 2012-10-12 states that each coupler curve can be generated by three different four-bar linkages. These four-bar linkages can be constructed using similar triangles and parallelograms, and the Cayley diagram (named after ). Overconstrained mechanism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cognate Linkages - Showcase
In historical linguistics, cognates or lexical cognates are sets of words that have been inherited in direct descent from an etymological ancestor in a common parent language. Because language change can have radical effects on both the sound and the meaning of a word, cognates may not be obvious, and it often takes rigorous study of historical sources and the application of the comparative method to establish whether lexemes are cognate. Cognates are distinguished from loanwords, where a word has been borrowed from another language. Name The English term ''cognate'' derives from Latin , meaning "blood relative". Examples An example of cognates from the same Indo-European root are: ''night'' (English), ''Nacht'' (German), ''nacht'' (Dutch, Frisian), ''nag'' (Afrikaans), ''Naach'' ( Colognian), ''natt'' (Swedish, Norwegian), ''nat'' ( Danish), ''nátt'' ( Faroese), ''nótt'' ( Icelandic), ''noc'' (Czech, Slovak, Polish), ночь, ''noch'' (Russian), ноќ, ''noć'' (Mace ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
De Casteljau's Algorithm
In the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau. De Casteljau's algorithm can also be used to split a single Bézier curve into two Bézier curves at an arbitrary parameter value. The algorithm is numerically stable when compared to direct evaluation of polynomials. The computational complexity of this algorithm is O(d n^2), where d is the number of dimensions, and n is the number of control points. There exist faster alternatives. Definition A Bézier curve B (of degree n, with control points \beta_0, \ldots, \beta_n) can be written in Bernstein form as follows B(t) = \sum_^\beta_b_(t), where b is a Bernstein basis polynomial b_(t) = (1-t)^t^i. The curve at point t_0 can be evaluated with the recurrence relation \begin \beta_i^ &:= \beta_i, && i=0,\ldots,n \\ \beta_i^ &:= \beta_i^ (1-t_0) + \beta_^ t_0, && i = 0,\ldots,n-j,\ \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kinematic Pair
In classical mechanics, a kinematic pair is a connection between two physical objects that imposes constraints on their relative movement (kinematics). German engineer Franz Reuleaux introduced the kinematic pair as a new approach to the study of machines that provided an advance over the notion of elements consisting of simple machines. Description Kinematics is the branch of classical mechanics which describes the motion of points, bodies (objects) and systems of bodies (groups of objects) without consideration of the causes of motion. Kinematics as a field of study is often referred to as the "geometry of motion". For further detail, see Kinematics. Hartenberg & Denavit presents the definition of a kinematic pair: In the matter of connections between rigid bodies, Reuleaux recognized two kinds; he called them higher and lower pairs (of elements). With higher pairs, the two elements are in contact at a point or along a line, as in a ball bearing or disk cam and follower; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cognate Linkages - Watt II Function Cognate Construction
In historical linguistics, cognates or lexical cognates are sets of words that have been inherited in direct descent from an etymological ancestor in a common parent language. Because language change can have radical effects on both the sound and the meaning of a word, cognates may not be obvious, and it often takes rigorous study of historical sources and the application of the comparative method to establish whether lexemes are cognate. Cognates are distinguished from loanwords, where a word has been borrowed from another language. Name The English term ''cognate'' derives from Latin , meaning "blood relative". Examples An example of cognates from the same Indo-European root are: ''night'' ( English), ''Nacht'' (German), ''nacht'' ( Dutch, Frisian), ''nag'' (Afrikaans), ''Naach'' ( Colognian), ''natt'' ( Swedish, Norwegian), ''nat'' ( Danish), ''nátt'' ( Faroese), ''nótt'' ( Icelandic), ''noc'' (Czech, Slovak, Polish), ночь, ''noch'' (Russian), ноќ, ''noć'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chebyshev Lambda Linkage
In kinematics, the Chebyshev Lambda Linkage is a four-bar linkage that converts rotational motion to approximate straight-line motion with approximate constant velocity. It is so-named because it looks like a lowercase Greek letter lambda (λ). The precise design trades off straightness, lack of acceleration, and the proportion of the driving rotation that is spent in the linear portion of the full curve. The example to the right spends over half of the cycle in the near-straight portion. The coupler (link 3) point stays within 1% positional tolerance while intersecting the ideal straight line 6 times. The linkage was first shown in Paris on the Exposition Universelle (1878) as "The Plantigrade Machine". The Chebyshev Lambda Linkage is a cognate linkage of the Chebyshev linkage. The Chebyshev Lambda Linkage is used in vehicle suspension mechanisms, walking robots, and rover wheel mechanisms. In 2004, a study completed as a Master of Science Thesis at Izmir Institute of Technol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chebyshev Linkage
In kinematics, Chebyshev's linkage is a four-bar linkage that converts rotational motion to approximate linear motion. It was invented by the 19th-century mathematician Pafnuty Chebyshev, who studied theoretical problems in kinematic Mechanism (engineering), mechanisms. One of the problems was the construction of a linkage that converts a rotary motion into an approximate straight-line motion (a straight line mechanism). This was also studied by James Watt in his improvements to the steam engine, which resulted in Watt's linkage. – Cross link straight-line mechanism Equations of motion The motion of the linkage can be constrained to an input angle that may be changed through velocities, forces, etc. The input angles can be either link ''L''2 with the horizontal or link ''L ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Five-bar Linkage
In kinematics, a five-bar linkage is a mechanism (engineering), mechanism with two Degrees of freedom (mechanics), degrees of freedom that is constructed from five links that are connected together in a Kinematic chain, closed chain. All links are connected to each other by five Kinematic pair, joints in series forming a loop. One of the links is the ground or base.Dong, Dianbiao, et al"Design and optimization of a powered ankle-foot prosthesis using a geared five-bar spring mechanism" ''International Journal of Advanced Robotic Systems'' 14.3 (2017): 1729881417704545. p. 3. This configuration is also called a pantograph,Campion, Gianni.The Pantograph Mk-II: a haptic instrument. The Synthesis of Three Dimensional Haptic Textures: Geometry, Control, and Psychophysics. Springer, London, 2005. 45-58. however, it is not to be confused with the parallelogram-copying linkage pantograph. The linkage can be a one-degree-of-freedom mechanism if two gears are attached to two links and ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cognate Linkages - 5-bar Geared Linkages
In historical linguistics, cognates or lexical cognates are sets of words that have been inherited in direct descent from an etymological ancestor in a common parent language. Because language change can have radical effects on both the sound and the meaning of a word, cognates may not be obvious, and it often takes rigorous study of historical sources and the application of the comparative method to establish whether lexemes are cognate. Cognates are distinguished from loanwords, where a word has been borrowed from another language. Name The English term ''cognate'' derives from Latin , meaning "blood relative". Examples An example of cognates from the same Indo-European root are: ''night'' (English), ''Nacht'' (German), ''nacht'' (Dutch, Frisian), ''nag'' (Afrikaans), ''Naach'' ( Colognian), ''natt'' (Swedish, Norwegian), ''nat'' ( Danish), ''nátt'' ( Faroese), ''nótt'' ( Icelandic), ''noc'' (Czech, Slovak, Polish), ночь, ''noch'' (Russian), ноќ, ''noć'' (Mace ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Law Of Sines
In trigonometry, the law of sines (sometimes called the sine formula or sine rule) is a mathematical equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, \frac \,=\, \frac \,=\, \frac \,=\, 2R, where , and are the lengths of the sides of a triangle, and , and are the opposite angles (see figure 2), while is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the Multiplicative inverse, reciprocals; \frac \,=\, \frac \,=\, \frac. The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data (called the ''ambiguous case'') and the technique gives two possible values for the enclosed angle. The law of sines is on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Similar Triangle
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (geometry), scaling (enlarging or reducing), possibly with additional translation (geometry), translation, rotation (mathematics), rotation and reflection (mathematics), reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruence (geometry), congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kinematics
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics. Kinematics is concerned with systems of specification of objects' positions and velocities and mathematical transformations between such systems. These systems may be rectangular like Cartesian coordinate system, cartesian, Curvilinear coordinates like polar coordinates or other systems. The object trajectories may be specified with respect to other objects which may themselve be in motion relative to a standard reference. Rotating systems may also be used. Numerous practical problems in kinematics involve constraints, such as mechanical linkages, ropes, or rolling disks. Overview Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, Physical object, bodies (objects), and systems of bodies (group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |