|
Channel Surface
In geometry and topology, a channel or canal surface is a surface formed as the Envelope (mathematics), envelope of a family of spheres whose centers lie on a space curve, its ''Generatrix, directrix''. If the radii of the generating spheres are constant, the canal surface is called a pipe surface. Simple examples are: * right circular cylinder (pipe surface, directrix is a line, the axis of the cylinder) * torus (pipe surface, directrix is a circle), * right circular cone (canal surface, directrix is a line (the axis), radii of the spheres not constant), * surface of revolution (canal surface, directrix is a line). Canal surfaces play an essential role in descriptive geometry, because in case of an orthographic projection its contour curve can be drawn as the envelope of circles. *In technical area canal surfaces can be used for ''blending surfaces'' smoothly. Envelope of a pencil of implicit surfaces Given the pencil of implicit surfaces :\Phi_c: f(,c)=0 , c\in [c_1,c_2], ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space V with finite Dimension (linear algebra), dimension is a Basis (linear algebra), basis for V whose vectors are orthonormal, that is, they are all unit vectors and Orthogonality_(mathematics), orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The Image (mathematics), image of the standard basis under a Rotation (mathematics), rotation or Reflection (mathematics), reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. An orthonormal basis can be derived from an orthogonal basis via Normalize (linear algebra), normalization. The choice of an origin (mathematics), origin and an orthonormal basis forms a coordinate frame known as an ''orthonormal frame''. For a general inner product space V, an orthono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Implicit Surface
In mathematics, an implicit surface is a Surface (geometry), surface in Euclidean space defined by an equation : F(x,y,z)=0. An ''implicit surface'' is the set of Zero of a function, zeros of a Function of several real variables, function of three variables. ''Implicit function, Implicit'' means that the equation is not solved for or or . The graph of a function is usually described by an equation z=f(x,y) and is called an ''explicit'' representation. The third essential description of a surface is the ''Parametric equation, parametric'' one: (x(s,t),y(s,t), z(s,t)), where the -, - and -coordinates of surface points are represented by three functions x(s,t)\, , y(s,t)\, , z(s,t) depending on common parameters s,t. Generally the change of representations is simple only when the explicit representation z=f(x,y) is given: z-f(x,y)=0 (implicit), (s,t,f(s,t)) (parametric). ''Examples'': #The Plane (geometry), plane x+2y-3z+1=0. #The Sphere (geometry), sphere x^2+y^2+z^2-4=0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Surface Of Revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersecting the generatrix, except at its endpoints). The volume bounded by the surface created by this revolution is the ''solid of revolution''. Examples of surfaces of revolution generated by a straight line are cylinder (geometry), cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
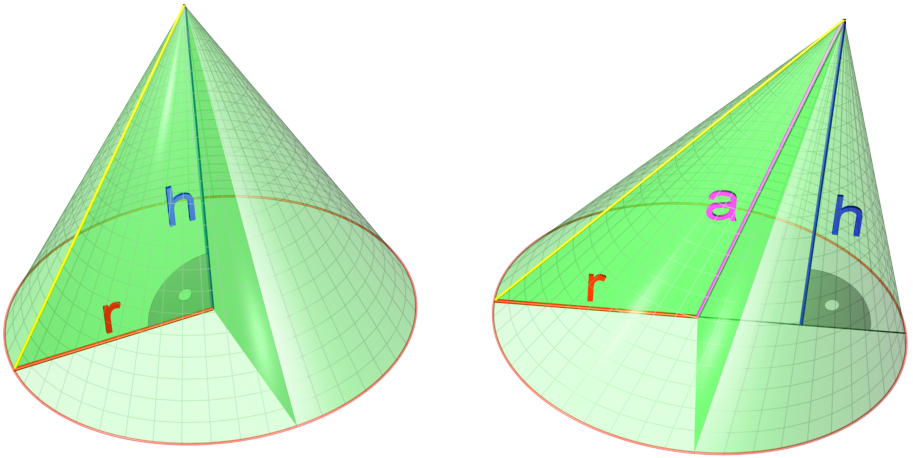
Right Circular Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Right Circular Cylinder
A right circular cylinder is a cylinder whose generatrices are perpendicular to the bases. Thus, in a right circular cylinder, the generatrix and the height have the same measurements. It is also less often called a cylinder of revolution, because it can be obtained by rotating a rectangle of sides r and g around one of its sides. Fixing g as the side on which the revolution takes place, we obtain that the side r, perpendicular to g, will be the measure of the radius of the cylinder. In addition to the right circular cylinder, within the study of spatial geometry there is also the '' oblique circular cylinder'', characterized by not having the geratrices perpendicular to the bases. Elements of the right circular cylinder Bases: the two parallel and congruent circles of the bases; Axis: the line determined by the two points of the centers of the cylinder's bases; Height: the distance between the two planes of the cylinder's bases; Generatrices: the line segments parallel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generatrix
In geometry, a generatrix () or describent is a point, curve or surface that, when moved along a given path, generates a new shape. The path directing the motion of the generatrix motion is called a directrix or dirigent. Examples A cone can be generated by moving a line (the generatrix) fixed at the future apex of the cone along a closed curve (the directrix); if that directrix is a circle perpendicular to the line connecting its center to the apex, the motion is rotation around a fixed axis and the resulting shape is a circular cone. The generatrix of a cylinder, a limiting case of a cone, is a line that is kept parallel to some axis. See also * Surface of revolution A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ... References Elementary geometry Computer graphics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |