|
Chain Rule (probability)
In probability theory, the chain rule (also called the general product rule) describes how to calculate the probability of the intersection of, not necessarily independent, events or the joint distribution of random variables respectively, using conditional probabilities. This rule allows one to express a joint probability in terms of only conditional probabilities. The rule is notably used in the context of discrete stochastic processes and in applications, e.g. the study of Bayesian networks, which describe a probability distribution in terms of conditional probabilities. Chain rule for events Two events For two events A and B, the chain rule states that :\mathbb P(A \cap B) = \mathbb P(B \mid A) \mathbb P(A), where \mathbb P(B \mid A) denotes the conditional probability of B given A. Example An Urn A has 1 black ball and 2 white balls and another Urn B has 1 black ball and 3 white balls. Suppose we pick an urn at random and then select a ball from that urn. Let event A be c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, h'(x) = f'(g(x)) g'(x). or, equivalently, h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as \frac = \frac \cdot \frac, and \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integral, integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
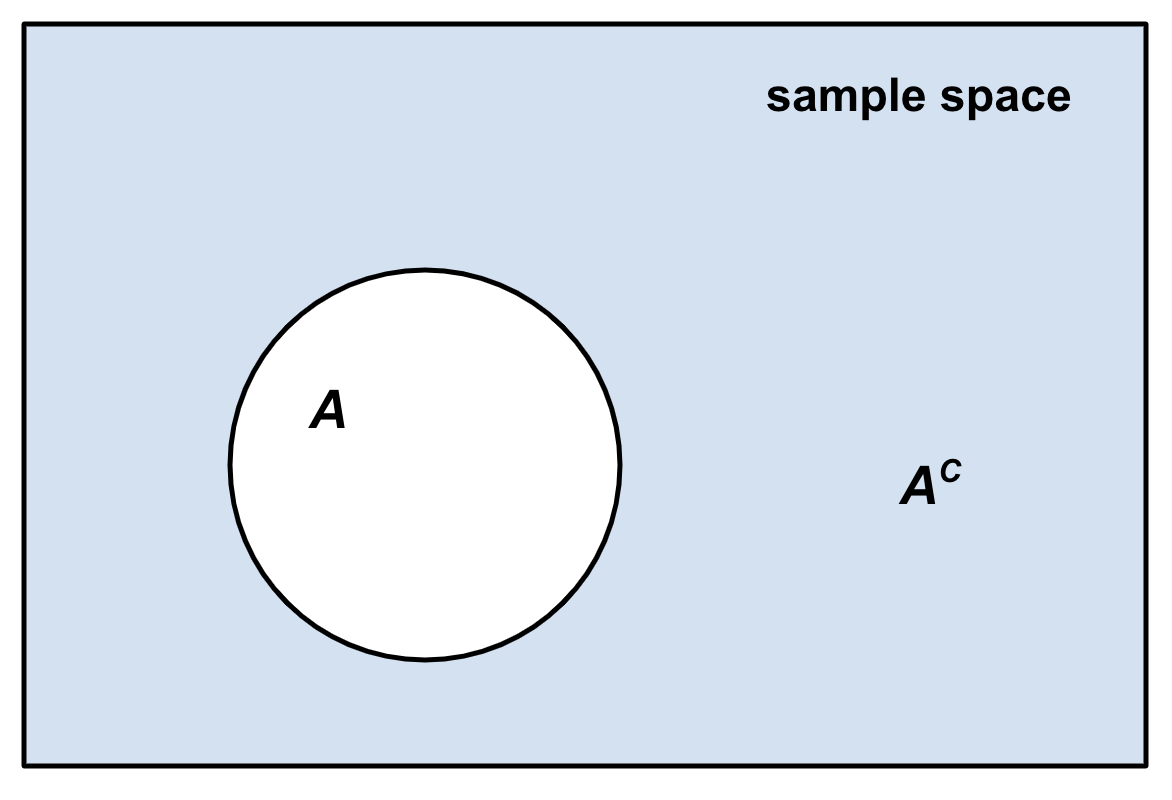
Complementary Event
In probability theory, the complement of any event ''A'' is the event ot ''A'' i.e. the event that ''A'' does not occur.Robert R. Johnson, Patricia J. Kuby: ''Elementary Statistics''. Cengage Learning 2007, , p. 229 () The event ''A'' and its complement ot ''A''are mutually exclusive and exhaustive. Generally, there is only one event ''B'' such that ''A'' and ''B'' are both mutually exclusive and exhaustive; that event is the complement of ''A''. The complement of an event ''A'' is usually denoted as ''A′'', ''Ac'', \neg''A'' or '. Given an event, the event and its complementary event define a Bernoulli trial: did the event occur or not? For example, if a typical coin is tossed and one assumes that it cannot land on its edge, then it can either land showing "heads" or "tails." Because these two outcomes are mutually exclusive (i.e. the coin cannot simultaneously show both heads and tails) and collectively exhaustive (i.e. there are no other possible outcom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics ( or ) is a theory in the field of statistics based on the Bayesian interpretation of probability, where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation, which views probability as the limit of the relative frequency of an event after many trials. More concretely, analysis in Bayesian methods codifies prior knowledge in the form of a prior distribution. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference ( or ) is a method of statistical inference in which Bayes' theorem is used to calculate a probability of a hypothesis, given prior evidence, and update it as more information becomes available. Fundamentally, Bayesian inference uses a prior distribution to estimate posterior probabilities. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Feller
William "Vilim" Feller (July 7, 1906 – January 14, 1970), born Vilibald Srećko Feller, was a Croatian–American mathematician specializing in probability theory. Early life and education Feller was born in Zagreb to Ida Oemichen-Perc, a Croatian–Austrian Catholic, and Eugen Viktor Feller, son of a Polish–Jewish father (David Feller) and an Austrian mother (Elsa Holzer). Eugen Feller was a famous chemist and created ''Elsa fluid'' named after his mother. According to Gian-Carlo Rota, Eugen Feller's surname was a "Slavic tongue twister", which William changed at the age of twenty. This claim appears to be false. His forename, Vilibald, was chosen by his Catholic mother for the saint day of his birthday. Career and later life Feller held a docent position at the University of Kiel beginning in 1928. Because he refused to sign a Nazi oath, he fled the Nazis and went to Copenhagen, Denmark in 1933. He also lectured in Sweden (Stockholm and Lund). As a refugee in Sweden, Fe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
René L
René (''born again'' or ''reborn'' in French) is a common first name in French-speaking, Spanish-speaking, and German-speaking countries. It derives from the Latin name Renatus. René is the masculine form of the name ( Renée being the feminine form). In some non-Francophone countries, however, there exists the habit of giving the name René (sometimes spelled without an accent) to girls as well as boys. In addition, both forms are used as surnames (family names). René as a first name given to boys in the United States reached its peaks in popularity in 1969 and 1983 when it ranked 256th. Since 1983 its popularity has steadily declined and it ranked 881st in 2016. René as a first name given to girls in the United States reached its peak in popularity in 1962 when it ranked 306th. The last year for which René was ranked in the top 1000 names given to girls in the United States was 1988. Persons with the given name * René, Duke of Anjou (1409–1480), titular king of Napl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability Distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Event (probability Theory)
In probability theory, an event is a subset of outcomes of an experiment (a subset of the sample space) to which a probability is assigned. A single outcome may be an element of many different events, and different events in an experiment are usually not equally likely, since they may include very different groups of outcomes. An event consisting of only a single outcome is called an or an ; that is, it is a singleton set. An event that has more than one possible outcome is called a compound event. An event S is said to if S contains the outcome x of the experiment (or trial) (that is, if x \in S). The probability (with respect to some probability measure) that an event S occurs is the probability that S contains the outcome x of an experiment (that is, it is the probability that x \in S). An event defines a complementary event, namely the complementary set (the event occurring), and together these define a Bernoulli trial: did the event occur or not? Typically, when the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Network
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases. Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (''e.g.'' speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |