|
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the exponents and are nonnegative integers with , and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in the term of is known as the binomial coefficient \tbinom or \tbinom (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where \tbinom gives the number of different combinations of elements that can be chosen from an -element set. Therefore \tbinom is often pronounced as " choose ". History Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid ment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the term in the polynomial expansion of the binomial power ; this coefficient can be computed by the multiplicative formula :\binom nk = \frac, which using factorial notation can be compactly expressed as :\binom = \frac. For example, the fourth power of is :\begin (1 + x)^4 &= \tbinom x^0 + \tbinom x^1 + \tbinom x^2 + \tbinom x^3 + \tbinom x^4 \\ &= 1 + 4x + 6 x^2 + 4x^3 + x^4, \end and the binomial coefficient \tbinom =\tfrac = \tfrac = 6 is the coefficient of the term. Arranging the numbers \tbinom, \tbinom, \ldots, \tbinom in successive rows for n=0,1,2,\ldots gives a triangular array called Pascal's triangle, satisfying the recurrence relation :\binom = \binom + \binom. The binomial coefficients occur in many areas of mathematics, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bhāskara II
Bhāskara II (c. 1114–1185), also known as Bhāskarāchārya ("Bhāskara, the teacher"), and as Bhāskara II to avoid confusion with Bhāskara I, was an Indian mathematician and astronomer. From verses, in his main work, Siddhānta Shiromani (सिद्धांतशिरोमणी), it can be inferred that he was born in 1114 in Vijjadavida (Vijjalavida) and living in the Sahyadri mountain ranges of Western Ghats, believed to be the town of Patan in Chalisgaon, located in present-day Khandesh region of Maharashtra by scholars. He is the only ancient mathematician who has been immortalized on a monument. In a temple in Maharashtra, an inscription supposedly created by his grandson Changadeva, lists Bhaskaracharya's ancestral lineage for several generations before him as well as two generations after him. Colebrooke who was the first European to translate (1817) Bhaskaracharya II's mathematical classics refers to the family as Maharashtrian Brahmins residing on the ban ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simon Stevin
Simon Stevin (; 1548–1620), sometimes called Stevinus, was a Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated various mathematical terms into Dutch, making it one of the few European languages in which the word for mathematics, '' wiskunde'' ('' wis'' and '' kunde'', i.e., "the knowledge of what is certain"), was not a loanword from Greek but a calque via Latin. He also replaced the word '' chemie'', the Dutch for chemistry, by '' scheikunde'' ("the art of separating"), made in analogy with ''wikt:en:wiskunde#Dutch, wiskunde''. Biography Very little is known with certainty about Simon Stevin's life, and what we know is mostly inferred from other recorded facts.E. J. Dijksterhuis (1970) ''Simon Stevin: Science in the Netherlands around 1600'', The Hague: Martinus Nijhoff Publishers, Dutch original 1943, 's-Gravenhage The exact birth date and the date ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia (; 1499/1500 – 13 December 1557) was an Italian mathematician, engineer (designing fortifications), a surveyor (of topography, seeking the best means of defense or offense) and a bookkeeper from the then Republic of Venice. He published many books, including the first Italian translations of Archimedes and Euclid, and an acclaimed compilation of mathematics. Tartaglia was the first to apply mathematics to the investigation of the paths of cannonballs, known as ballistics, in his ''Nova Scientia'' (''A New Science'', 1537); his work was later partially validated and partially superseded by Galileo's studies on falling bodies. He also published a treatise on retrieving sunken ships. Personal life Niccolò Fontana was born in Brescia, the son of Michele Fontana, a dispatch rider who travelled to neighbouring towns to deliver mail. In 1506, Michele was murdered by robbers, and Niccolò, his two siblings, and his mother were left impoverished. Niccol� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blaise Pascal
Blaise Pascal ( , , ; ; 19 June 1623 – 19 August 1662) was a French mathematician, physicist, inventor, philosopher, and Catholic Church, Catholic writer. He was a child prodigy who was educated by his father, a tax collector in Rouen. Pascal's earliest mathematical work was on conic sections; he wrote a significant treatise on the subject of projective geometry at the age of 16. He later corresponded with Pierre de Fermat on probability theory, strongly influencing the development of modern economics and social sciences, social science. In 1642, while still a teenager, he started some pioneering work on calculating machines (called Pascal's calculators and later Pascalines), establishing him as one of the first two inventors of the mechanical calculator. Like his contemporary René Descartes, Pascal was also a pioneer in the natural and applied sciences. Pascal wrote in defense of the scientific method and produced several controversial results. He made important contribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Stifel
Michael Stifel or Styfel (1487 – April 19, 1567) was a German monk, Protestant reformer and mathematician. He was an Augustinian who became an early supporter of Martin Luther. He was later appointed professor of mathematics at Jena University. Life Stifel was born in Esslingen am Neckar in southern Germany. He joined the Order of Saint Augustine and was ordained a priest in 1511. Tensions in the abbey grew after he published the poem ''Von der Christförmigen, rechtgegründeten leer Doctoris Martini Luthers'' (1522, i.e. On the Christian, righteous doctrine of Doctor Martin Luther) and came into conflict with Thomas Murner. Stifel then left for Frankfurt, and soon went to Mansfeld, where he began his mathematical studies. In 1524, upon a recommendation by Luther, Stifel was called by the Jörger family to serve at their residence, Tollet Castle in Tollet (close to Grieskirchen, Upper Austria). Due to the tense situation in the Archduchy of Austria in the wake of the execu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
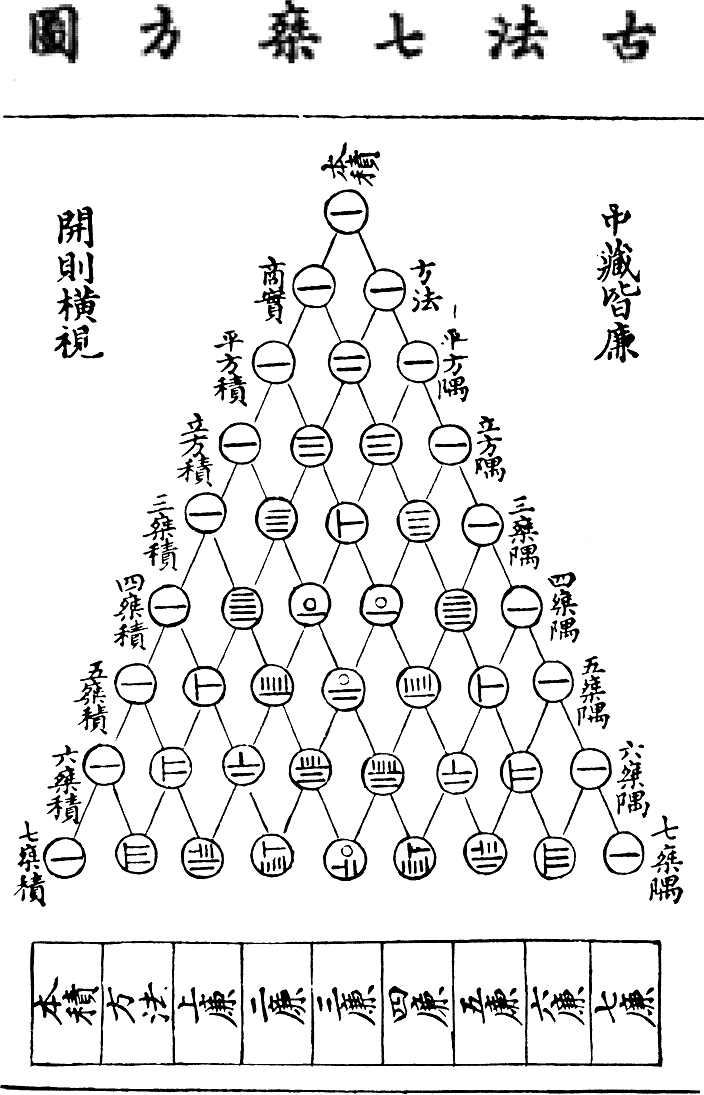
Jia Xian
Jia Xian (; ca. 1010–1070) was a Chinese mathematician from Kaifeng of the Song dynasty. Biography According to the history of the Song dynasty, Jia was a palace eunuch of the Left Duty Group. He studied under the mathematician Chu Yan, and was well versed in mathematics, writing many books on the subject. Jia Xian described the Pascal's triangle (Jia Xian triangle) around the middle of the 11th century, about six centuries before Pascal. Jia used it as a tool for extracting square and cubic roots. The original book by Jia entitled ''Shi Suo Suan Shu'' was lost; however, Jia's method was expounded in detail by Yang Hui, who explicitly acknowledged his source: "My method of finding square and cubic roots was based on the Jia Xian method in ''Shi Suo Suan Shu''." A page from the ''Yongle Encyclopedia The ''Yongle Encyclopedia'' () or ''Yongle Dadian'' () is a largely-lost Chinese ''leishu'' encyclopedia commissioned by the Yongle Emperor of the Ming dynasty in 1403 and compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chu Shih-Chieh
Zhu Shijie (, 1249–1314), courtesy name Hanqing (), pseudonym Songting (), was a Chinese mathematician and writer. He was a Chinese mathematician during the Yuan Dynasty. Zhu was born close to today's Beijing. Two of his mathematical works have survived. ''Introduction to Computational Studies'' ( ''Suan hsüeh Ch'i-mong''), and ''Jade Mirror of the Four Unknowns''. ''Suanxue qimeng'' The ''Suan hsüeh Ch'i-mong'' (), written in 1299, is an elementary textbook on mathematics in three volumes, 20 chapters and 259 problems. This book also showed how to measure different two-dimensional shapes and three-dimensional solids. The ''Introduction'' had an important influence on the development of mathematics in Japan. The book was once lost in China until Qing dynasty mathematician Luo Shilin bought a Korean printed edition, and re-published in Yangzhou. Since then this book was reprinted several times. ''Jade Mirror of the Four Unknowns'' Zhu's second book, ''Jade Mirror of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yang Hui
Yang Hui (, ca. 1238–1298), courtesy name Qianguang (), was a Chinese mathematician and writer during the Song dynasty. Originally, from Qiantang (modern Hangzhou, Zhejiang), Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting Yang Hui's Triangle. This triangle was the same as Pascal's Triangle, discovered by Yang's predecessor Jia Xian. Yang was also a contemporary to the other famous mathematician Qin Jiushao. Written work The earliest extant Chinese illustration of 'Pascal's triangle' is from Yang's book ''Xiangjie Jiuzhang Suanfa'' ()Fragments of this book was retained in the Yongle Encyclopedia vol 16344, in British Museum Library of 1261 AD, in which Yang acknowledged that his method of finding square roots and cubic roots using "Yang Hui's Triangle" was invented by mathematician Jia XianNeedham, Volume 3, 134-137. who expounded it around 1100 AD, about 500 years before Pascal. In his book (now los ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a polymath, known for his contributions to mathematics, astronomy, philosophy, and Persian poetry. He was born in Nishapur, the initial capital of the Seljuk Empire. As a scholar, he was contemporary with the rule of the Seljuk dynasty around the time of the First Crusade. As a mathematician, he is most notable for his work on the classification and solution of cubic equations, where he provided geometric solutions by the intersection of conics. Khayyam also contributed to the understanding of the parallel axiom.Struik, D. (1958). "Omar Khayyam, mathematician". ''The Mathematics Teacher'', 51(4), 280–285. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar, a solar calendar with a very precise 33-year intercalation cycle''The Cam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for ''n'' = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case ''n'' = ''k'', ''then'' it must also hold for the next case ''n'' = ''k'' + 1. These two steps establish that the statement holds for every natural number ''n''. The base case does not necessarily begin with ''n'' = 0, but often with ''n'' = 1, and possibly with any fixed natural number ''n'' = ''N'', establishing the truth of the statement for all natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)