|
Batch Normalization
Batch normalization (also known as batch norm) is a method used to make training of artificial neural networks faster and more stable through normalization of the layers' inputs by re-centering and re-scaling. It was proposed by Sergey Ioffe and Christian Szegedy in 2015. While the effect of batch normalization is evident, the reasons behind its effectiveness remain under discussion. It was believed that it can mitigate the problem of ''internal covariate shift'', where parameter initialization and changes in the distribution of the inputs of each layer affect the learning rate of the network. Recently, some scholars have argued that batch normalization does not reduce internal covariate shift, but rather smooths the objective function, which in turn improves the performance. However, at initialization, batch normalization in fact induces severe gradient explosion in deep networks, which is only alleviated by skip connections in residual networks. Others maintain that batch nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Neural Network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains. An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called ''edges''. Neurons and edges typically have a '' weight'' that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lipschitz Continuity
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the ''Lipschitz constant'' of the function (or '' modulus of uniform continuity''). For instance, every function that has bounded first derivatives is Lipschitz continuous. In the theory of differential equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to an initial value problem. A special type of Lipschitz continuity, called contraction, is used in the Banach fixed-point theorem. We have the following chain of strict inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilayer Perceptron
A multilayer perceptron (MLP) is a fully connected class of feedforward artificial neural network (ANN). The term MLP is used ambiguously, sometimes loosely to mean ''any'' feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons (with threshold activation); see . Multilayer perceptrons are sometimes colloquially referred to as "vanilla" neural networks, especially when they have a single hidden layer. An MLP consists of at least three layers of nodes: an input layer, a hidden layer and an output layer. Except for the input nodes, each node is a neuron that uses a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training. Its multiple layers and non-linear activation distinguish MLP from a linear perceptron. It can distinguish data that is not linearly separable.Cybenko, G. 1989. Approximation by superpositions of a sigmoidal function '' Mathematics of Control, Signals, and Systems'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bisection Algorithm
In mathematics, the bisection method is a root-finding method that applies to any continuous function for which one knows two values with opposite signs. The method consists of repeatedly bisecting the interval defined by these values and then selecting the subinterval in which the function changes sign, and therefore must contain a root. It is a very simple and robust method, but it is also relatively slow. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods. The method is also called the interval halving method, the binary search method, or the dichotomy method. For polynomials, more elaborate methods exist for testing the existence of a root in an interval (Descartes' rule of signs, Sturm's theorem, Budan's theorem). They allow extending the bisection method into efficient algorithms for finding all real roots of a polynomial; see Real-root isolation. The method The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades. Description Gradient descent is based on the observation that if the multi-variable function F(\mathbf) is de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
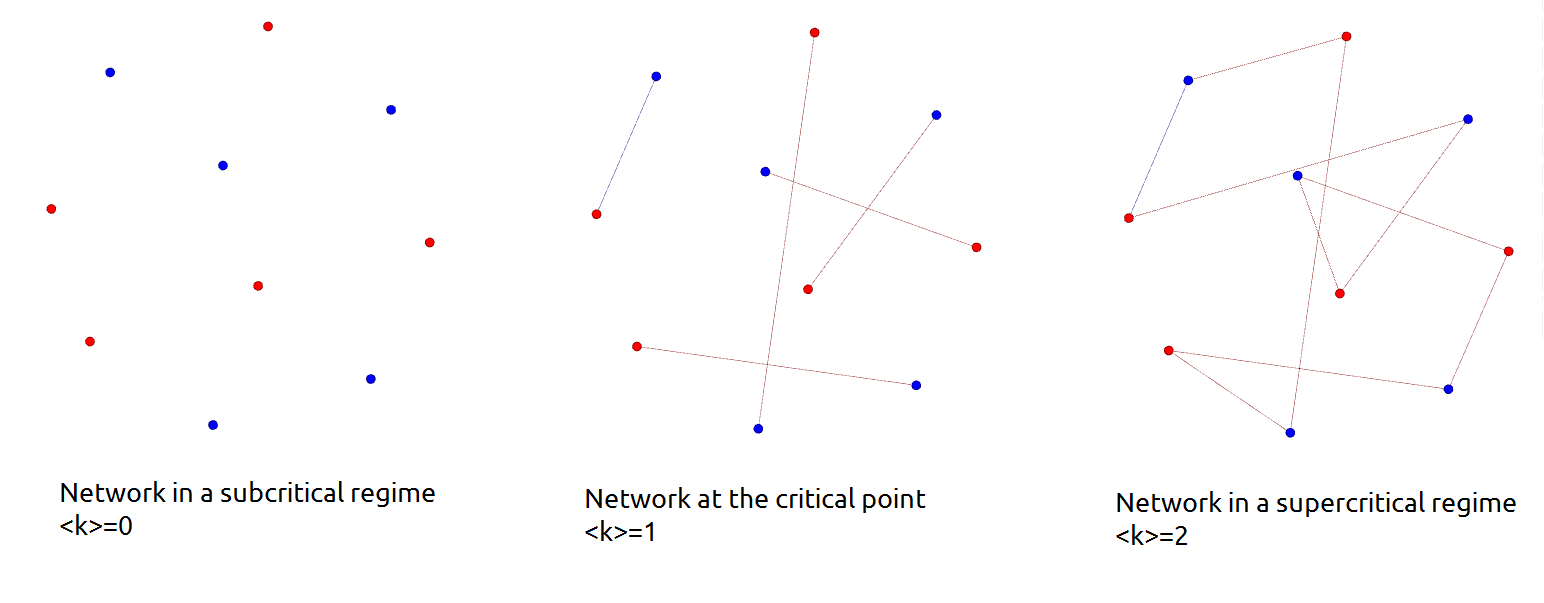
Critical Point (network Science)
In network science, a critical point is a value of average degree, which separates random networks that have a giant component from those that do not (i.e. it separates a network in a subcritical regime from one in a supercritical regime). Considering a random network with an average degree \langle k\rangle the critical point is \langle k\rangle = 1 where the average degree is defined by the fraction of the number of edges (e) and nodes (N) in the network, that is \langle k\rangle =\frac. Subcritical regime In a subcritical regime the network has no giant component, only small clusters. In the special case of \langle k\rangle =0 the network is not connected at all. A random network is in a subcritical regime until the average degree exceeds the critical point, that is the network is in a subcritical regime as long as \langle k\rangle 1. Example on different regimes Consider a speed dating event as an example, with the participants as the nodes of the network. At the begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothness
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain, called ''differentiability class''. At the very minimum, a function could be considered smooth if it is differentiable everywhere (hence continuous). At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function (or C^ function). Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an open set U on the real line and a function f defined on U with real values. Let ''k'' be a non-negative integer. The function f is said to be of differentiability class ''C^k'' if the derivatives f',f'',\dots,f^ exist and are continuous on U. If f is k-diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. History The perceptron was invented in 1943 by McCulloch and Pitts. The first implementation was a machine built in 1958 at the Cornell Aeronautical Laboratory by Frank Rosenblatt, funded by the United States Office of Naval Research. The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the "Mark 1 perceptron". This machine was designed for image recognition: it had an array of 400 photoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic roo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rayleigh Quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix ''M'' and nonzero vector ''x'' is defined as: R(M,x) = . For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugate transpose x^ to the usual transpose x'. Note that R(M, c x) = R(M,x) for any non-zero scalar ''c''. Recall that a Hermitian (or real symmetric) matrix is diagonalizable with only real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value \lambda_\min (the smallest eigenvalue of ''M'') when ''x'' is v_\min (the corresponding eigenvector). Similarly, R(M, x) \leq \lambda_\max and R(M, v_\max) = \lambda_\max. The Rayleigh quotient is used in the min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms (such as Rayleigh quotient iteration) to obtain an eigenvalue approximation from an eigenvector approximation. The range of the Rayleigh qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definiteness
In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular: * Positive-definite bilinear form * Positive-definite function * Positive-definite function on a group * Positive-definite functional * Positive-definite kernel * Positive-definite matrix In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a ... * Positive-definite quadratic form References *. *. {{Set index article, mathematics Quadratic forms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |