|
Bending Oscillators
In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two.Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials, John Wiley and Sons, New York. When the length is considerably longer than the width and the thickness, the element is called a beam. For example, a closet rod sagging under the weight of clothes on clothes hangers is an example of a beam experiencing bending. On the other hand, a shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
I Beam Bending0
I, or i, is the ninth letter and the third vowel letter of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''i'' (pronounced ), plural ''ies''. Name In English, the name of the letter is the "long I" sound, pronounced . In most other languages, its name matches the letter's pronunciation in open syllables. History In the Phoenician alphabet, the letter may have originated in a hieroglyph for an arm that represented a voiced pharyngeal fricative () in Egyptian, but was reassigned to (as in English "yes") by Semites because their word for "arm" began with that sound. This letter could also be used to represent , the close front unrounded vowel, mainly in foreign words. The Greeks adopted a form of this Phoenician ''yodh'' as their letter ''iota'' () to represent , the same as in the Old Italic alphabet. In Latin (as in Modern Greek), it was also used to represent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
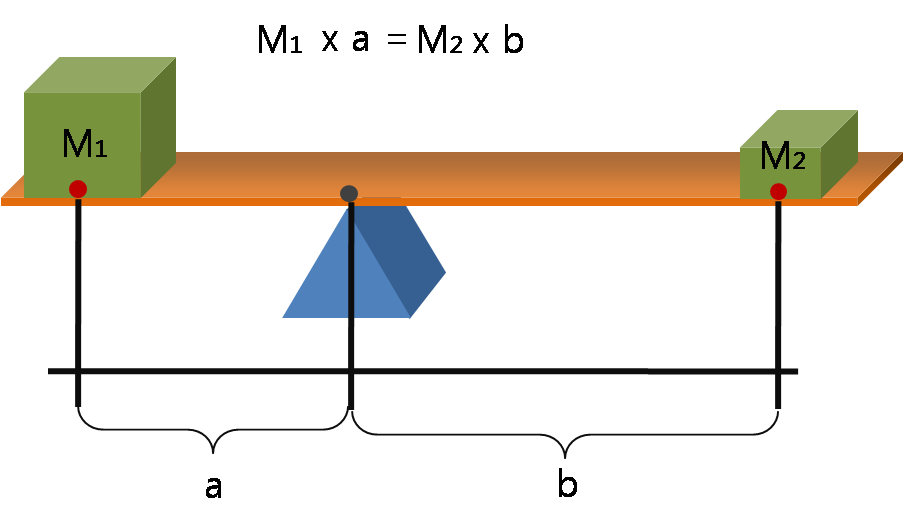
Moment (physics)
A moment is a mathematical expression involving the product of a distance and a physical quantity such as a force or electric charge. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions; a list of examples is provided later. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area Moment Of Inertia
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its physical unit, unit of dimension, when working with the International System of Units, is meters to the fourth power, metre, m4, or inches to the fourth power, inch, in4, when working in the Imperial units, Imperial System of Units or the US customary system. In structural engineering, the second moment of area of a beam (structure), beam is an important property used in the calculation of the beam's deflection (engineering), deflection and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress (force per unit area) applied to the object and the resulting axial strain (displacement or deformation) in the linear elastic region of the material. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years. The term modulus is derived from the Latin root term '' modus'', which means ''measure''. Definition Young's modulus, E, quantifies the relationship between tensile or compressive stress \sigma (force per unit ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous
Homogeneity and heterogeneity are concepts relating to the uniformity of a substance, process or image. A homogeneous feature is uniform in composition or character (i.e., color, shape, size, weight, height, distribution, texture, language, income, disease, temperature, radioactivity, architectural design, etc.); one that is heterogeneous is distinctly nonuniform in at least one of these qualities. Etymology and spelling The words ''homogeneous'' and ''heterogeneous'' come from Medieval Latin ''homogeneus'' and ''heterogeneus'', from Ancient Greek ὁμογενής (''homogenēs'') and ἑτερογενής (''heterogenēs''), from ὁμός (''homos'', "same") and ἕτερος (''heteros'', "other, another, different") respectively, followed by γένος (''genos'', "kind"); -ous is an adjectival suffix. Alternate spellings omitting the last ''-e-'' (and the associated pronunciations) are common, but mistaken: ''homogenous'' is strictly a biological/pathological term whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
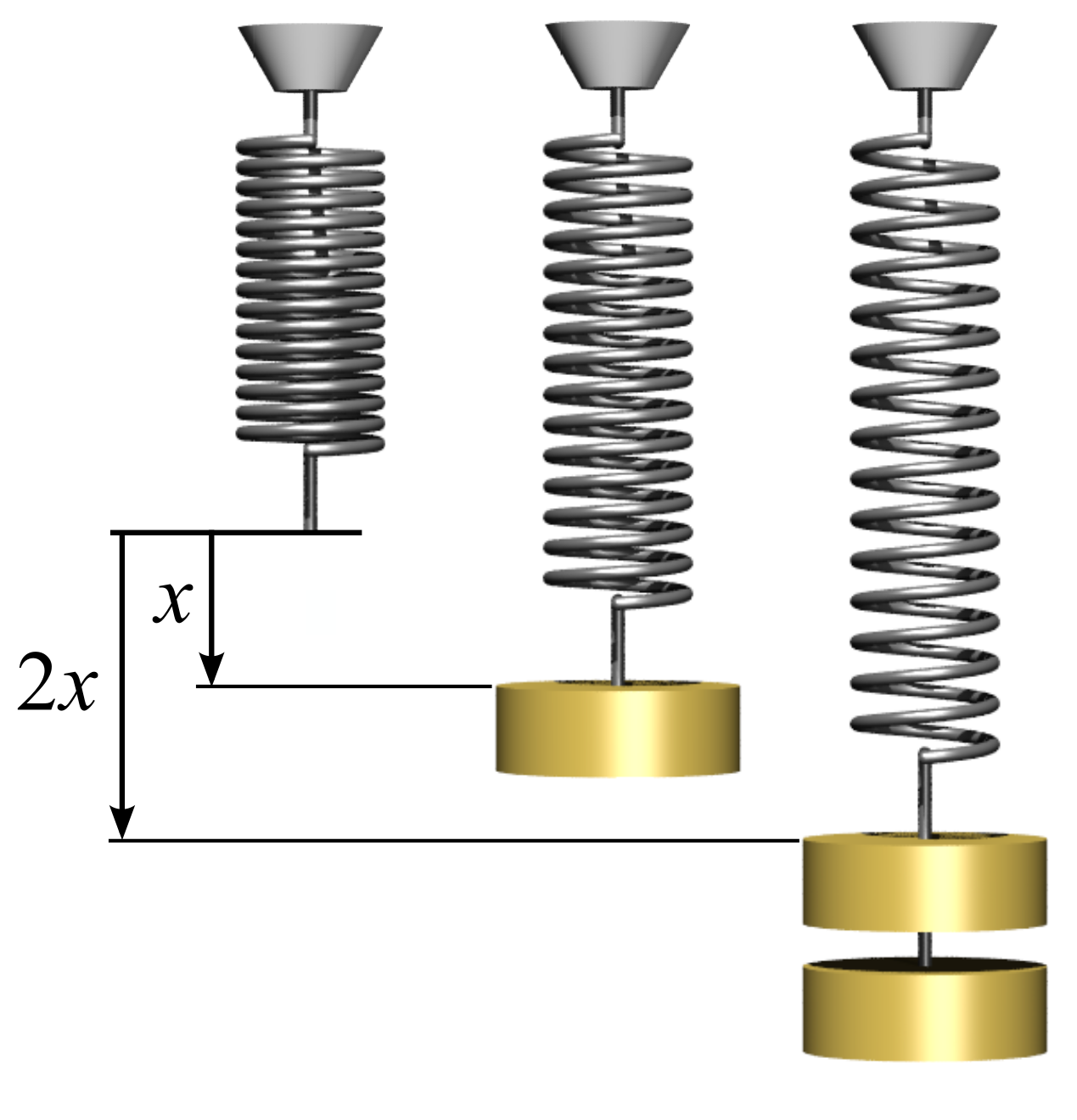
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthotropic Material
In material science and solid mechanics, orthotropic materials have material properties at a particular point which differ along three orthogonal axes, where each axis has twofold rotational symmetry. These directional differences in strength can be quantified with Hankinson's equation. They are a subset of anisotropic materials, because their properties change when measured from different directions. A familiar example of an orthotropic material is wood. In wood, one can define three mutually perpendicular directions at each point in which the properties are different. It is most stiff (and strong) along the grain (axial direction), because most cellulose fibrils are aligned that way. It is usually least stiff in the radial direction (between the growth rings), and is intermediate in the circumferential direction. This anisotropy was provided by evolution, as it best enables the tree to remain upright. Because the preferred coordinate system is cylindrical-polar, this type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the Stress (mechanics), stress in a material just before it Yield (engineering), yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutral Axis
The neutral axis is an axis in the cross section of a beam (a member resisting bending) or shaft along which there are no longitudinal stresses or strains. Theory If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid of a beam or shaft. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression. Since the beam is undergoing uniform bending, a plane on the beam remains plane. That is: \gamma_=\gamma_=\tau_=\tau_=0 Where \gamma is the shear strain and \tau is the shear stress There is a compressive (negative) strain at the top of the beam, and a tensile (positive) strain at the bottom of the beam. Therefore, by the Intermediate Value Theorem, there must be some point in between the top and the bottom that has no strain, since the strain in a beam is a continuous function. Let L be the original length of the beam ( span) ε(y) is the stra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plastic Bending
{{Short description, Behavior of some ductile materials Plastic bending is a nonlinear behavior particular to members made of ductile materials that frequently achieve much greater ultimate bending strength than indicated by a linear elastic bending analysis. In both the plastic and elastic bending analyses of a straight beam, it is assumed that the strain distribution is linear about the neutral axis (plane sections remain plane). In an elastic analysis this assumption leads to a linear stress distribution but in a plastic analysis the resulting stress distribution is nonlinear and is dependent on the beam's material. The limiting plastic bending strength M_r (see Plastic moment) can generally be thought of as an upper limit to a beam's load–carrying capability as it only represents the strength at a particular cross–section and not the load–carrying capability of the overall beam. A beam may fail due to global or local instability before M_r is reached at any point on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yield Stress
In materials science and engineering, the yield point is the point on a stress–strain curve that indicates the limit of elasticity (physics), elastic behavior and the beginning of plasticity (physics), plastic behavior. Below the yield point, a material will deformation (engineering)#elastic deformation, deform elastically and will return to its original shape when the applied stress (mechanics), stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as Deformation (engineering)#plastic deformation, plastic deformation. The yield strength or yield stress is a List of materials properties, material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable Structural load, load in a mechanical component, since it represents the upper limit to forces that can be applied without pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |