|
Autonomous System (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable. When the variable is time, they are also called time-invariant systems. Many laws in physics, where the independent variable is usually assumed to be time, are expressed as autonomous systems because it is assumed the laws of nature which hold now are identical to those for any point in the past or future. Definition An autonomous system is a system of ordinary differential equations of the form \fracx(t)=f(x(t)) where takes values in -dimensional Euclidean space; is often interpreted as time. It is distinguished from systems of differential equations of the form \fracx(t)=g(x(t),t) in which the law governing the evolution of the system does not depend solely on the system's current state but also the parameter , again often interpreted as time; such systems are by definition not autonomous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
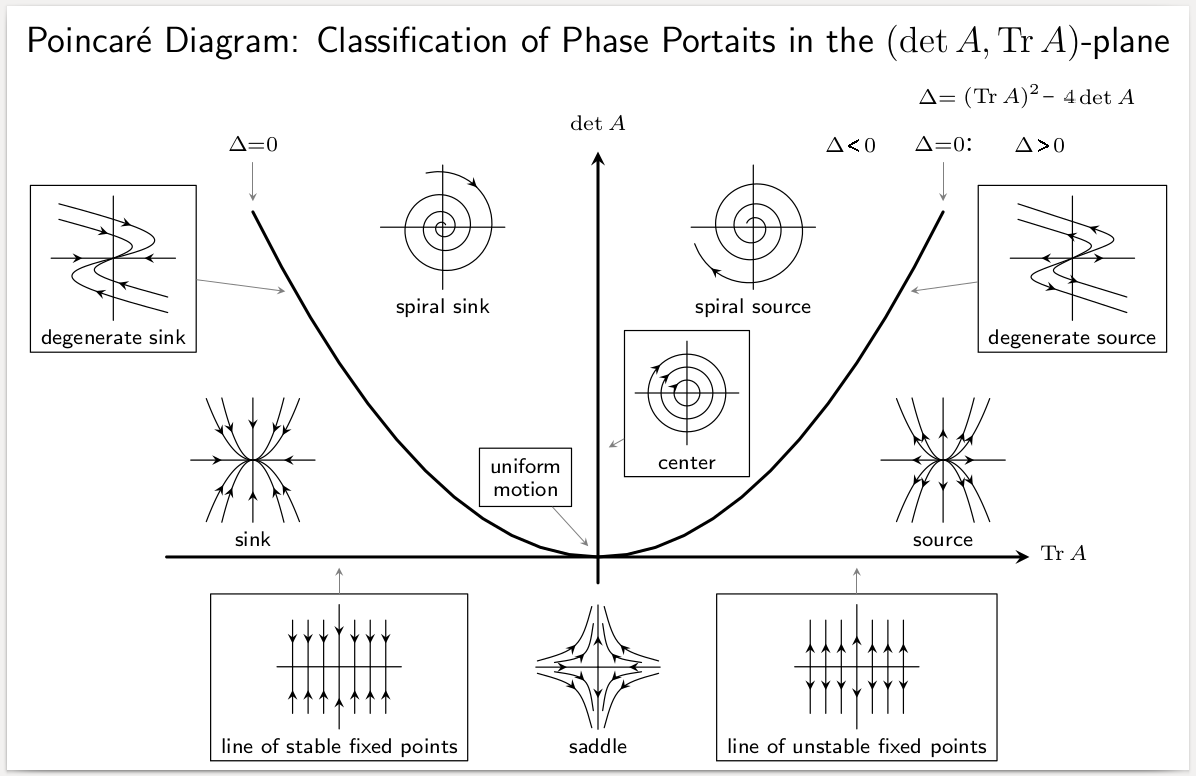
Stability Diagram
Stability may refer to: Mathematics *Stability theory, the study of the stability of solutions to differential equations and dynamical systems **Asymptotic stability **Linear stability **Lyapunov stability **Orbital stability **Structural stability *Stability (probability), a property of probability distributions *Stability (learning theory), a property of machine learning algorithms *Stability, a property of Stable sorting algorithm, sorting algorithms *Numerical stability, a property of numerical algorithms which describes how errors in the input data propagate through the algorithm *Stability radius, a property of continuous polynomial functions *Stable theory, concerned with the notion of stability in model theory *Stability, a property of points in Stable point, geometric invariant theory *K-Stability, a stability condition for algebraic varieties. *Bridgeland stability conditions, a class of stability conditions on elements of a triangulated category. *Stability (algebraic geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by findin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Differential Equation
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x) where and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of an unknown function of the variable . Such an equation is an ordinary differential equation (ODE). A ''linear differential equation'' may also be a linear partial differential equation (PDE), if the unknown function depends on several variables, and the derivatives that appear in the equation are partial derivatives. A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature, which means that the solutions may be expressed in terms of integrals. This is also true for a linear equation of order one, with non-co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division By Zero
In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as \tfrac, where is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number that, when multiplied by , gives (assuming a \neq 0); thus, division by zero is undefined. Since any number multiplied by zero is zero, the expression \tfrac is also undefined; when it is the form of a limit, it is an indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to \tfrac is contained in Anglo-Irish philosopher George Berkeley's criticism of infinitesimal calculus in 1734 in '' The Analyst'' ("ghosts of departed quantities"). There are mathematical structures in which \tfrac is defined for some such as in the Riemann sphere (a model of the extended complex plane) and the Projectively extended real line; however, such structures do not satisf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian System
A Hamiltonian system is a dynamical system governed by Hamilton's equations. In physics, this dynamical system describes the evolution of a physical system such as a planetary system or an electron in an electromagnetic field. These systems can be studied in both Hamiltonian mechanics and dynamical systems theory. Overview Informally, a Hamiltonian system is a mathematical formalism developed by Hamilton to describe the evolution equations of a physical system. The advantage of this description is that it gives important insights into the dynamics, even if the initial value problem cannot be solved analytically. One example is the planetary movement of three bodies: while there is no closed-form solution to the general problem, Poincaré showed for the first time that it exhibits deterministic chaos. Formally, a Hamiltonian system is a dynamical system characterised by the scalar function H(\boldsymbol,\boldsymbol,t), also known as the Hamiltonian. The state of the system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical mechanics, if the present state is known, it is possible to predict how it will move in the future (determinism), and how it has moved in the past (reversibility). The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on foundational works of Sir Isaac Newton, and the mathematical methods invented by Gottfried Wilhelm Leibniz, Joseph-Louis Lagrange, Leonhard Euler, and other contemporaries, in the 17th century to describe the motion of bodies under the influence of a system of forces. Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, :h'(x) = f'(g(x)) g'(x). or, equivalently, :h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as :\frac = \frac \cdot \frac, and : \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing the instantaneous rate of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Derivative
In calculus, the second derivative, or the second order derivative, of a function is the derivative of the derivative of . Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of the object is changing with respect to time. In Leibniz notation: :\mathbf = \frac = \frac, where ''a'' is acceleration, ''v'' is velocity, ''t'' is time, ''x'' is position, and d is the instantaneous "delta" or change. The last expression \tfrac is the second derivative of position (x) with respect to time. On the graph of a function, the second derivative corresponds to the curvature or concavity of the graph. The graph of a function with a positive second derivative is upwardly concave, while the graph of a function with a negative second derivative curves in the opposite way ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Examples Of Differential Equations
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Line (mathematics)
In mathematics, a phase line is a diagram that shows the qualitative behaviour of an autonomous ordinary differential equation in a single variable, \tfrac = f(y). The phase line is the 1-dimensional form of the general n-dimensional phase space, and can be readily analyzed. Diagram A line, usually vertical, represents an interval of the domain of the derivative. The critical points (i.e., roots of the derivative \tfrac, points y such that f(y) = 0) are indicated, and the intervals between the critical points have their signs indicated with arrows: an interval over which the derivative is positive has an arrow pointing in the positive direction along the line (up or right), and an interval over which the derivative is negative has an arrow pointing in the negative direction along the line (down or left). The phase line is identical in form to the line used in the first derivative test, other than being drawn vertically instead of horizontally, and the interpretation is virtuall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |