|
Affirming A Disjunct
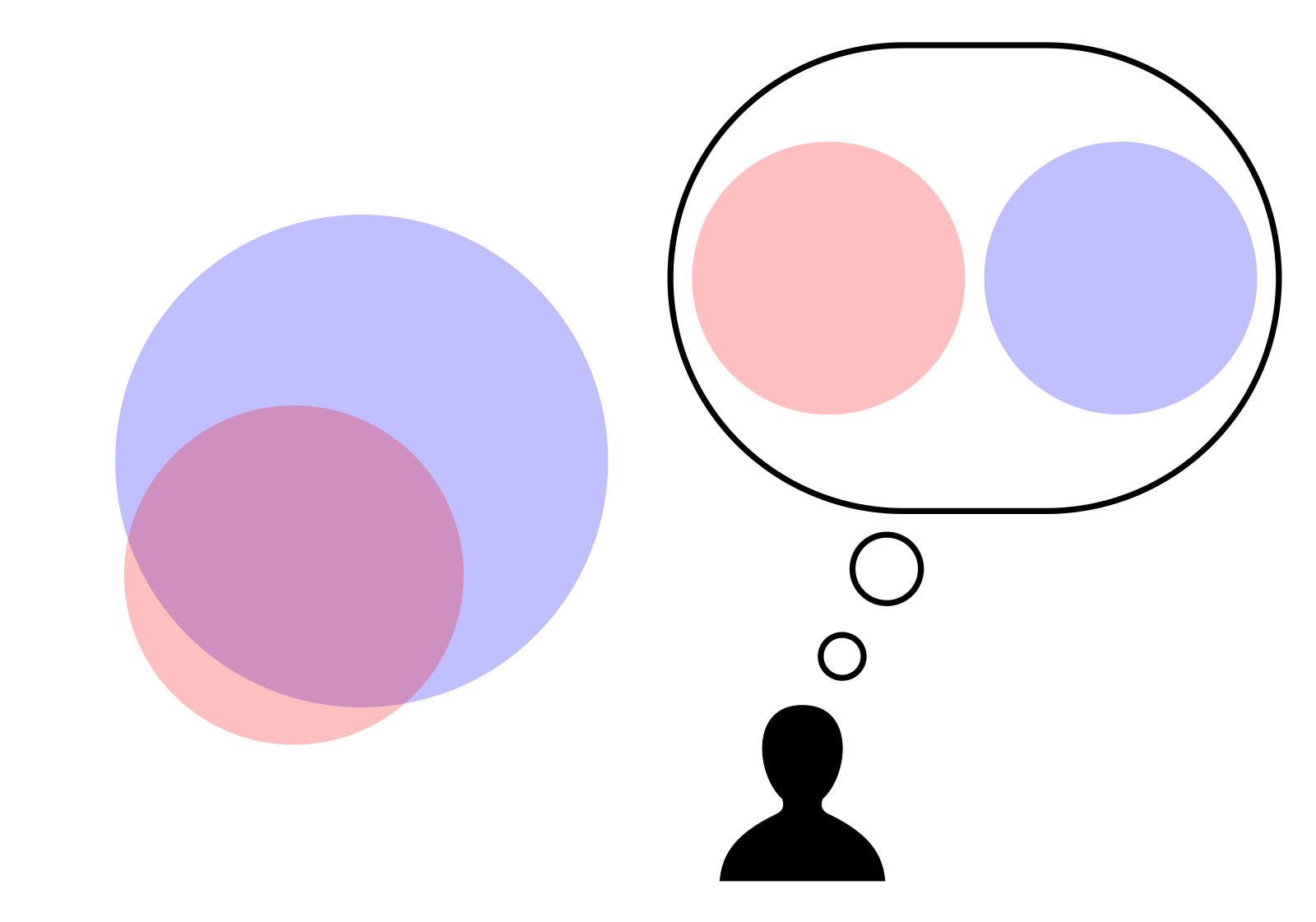
The formal fallacy of affirming a disjunct also known as the fallacy of the alternative disjunct or a false exclusionary disjunct occurs when a deductive argument takes the following logical form: :A or B :A :Therefore, not B Or in logical operators: : p \vee q : p : \vdash ¬ q Where \vdash denotes a logical assertion. Explanation The fallacy lies in concluding that one disjunct must be false because the other disjunct is true; in fact they may both be true because "or" is defined inclusively rather than exclusively. It is a fallacy of equivocation between the operations OR and XOR. Affirming the disjunct should not be confused with the valid argument known as the disjunctive syllogism. Examples The following argument indicates the unsoundness of affirming a disjunct: :Max is a mammal or Max is a cat. :Max is a mammal. :Therefore, Max is not a cat. This inference is unsound because all cats, by definition, are mammals. A second example provides a first pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous non-classical treatments, motivated by problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syllogistic Fallacy
A syllogism (, ''syllogismos'', 'conclusion, inference') is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true. In its earliest form (defined by Aristotle in his 350 BC book '' Prior Analytics''), a deductive syllogism arises when two true premises (propositions or statements) validly imply a conclusion, or the main point that the argument aims to get across. For example, knowing that all men are mortal (major premise), and that Socrates is a man (minor premise), we may validly conclude that Socrates is mortal. Syllogistic arguments are usually represented in a three-line form: All men are mortal. Socrates is a man. Therefore, Socrates is mortal.In antiquity, two rival syllogistic theories existed: Aristotelian syllogism and Stoic syllogism. From the Middle Ages onwards, ''categorical syllogism'' and ''syllogism'' were usually used interchangeably. This article is concerne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous non-classical treatments, motivated by problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exclusive Disjunction
Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or Logical_equality#Inequality, logical inequality is a Logical connective, logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ (one is true, one is false). With multiple inputs, XOR is true if and only if the number of true inputs is Parity (mathematics), odd. It gains the name "exclusive or" because the meaning of "or" is ambiguous when both operands are true. XOR ''excludes'' that case. Some informal ways of describing XOR are "one or the other but not both", "either one or the other", and "A or B, but not A and B". It is Table of logic symbols, symbolized by the prefix operator J Translated as and by the infix operators XOR (, , or ), EOR, EXOR, \dot, \overline, \underline, ⩛, \oplus, \nleftrightarrow, and \not\equiv. Definition The truth table of A\nleftrightarrow B shows that it outputs true whenever the inpu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vogue (magazine)
''Vogue'' (stylized in all caps), also known as American ''Vogue'', is a monthly Fashion journalism, fashion and lifestyle magazine that covers style news, including haute couture fashion, beauty, culture, living, and Fashion show#Catwalk, runway. It is part of the global collection of Condé Nast's VOGUE media. Headquartered at One World Trade Center in the FiDi, Financial District of Lower Manhattan, ''Vogue'' began in 1892 as a weekly newspaper before becoming a monthly magazine years later. Since its founding, ''Vogue'' has featured numerous actors, musicians, models, athletes, and other prominent celebrities. British Vogue, British ''Vogue'', launched in 1916, was the first international edition, while the Italian version ''Vogue Italia'' has been called the top fashion magazine in the world. As of March 2025, there are 28 international editions. Eleven of these editions are published by Condé Nast (British Vogue, ''British Vogue'', ''Vogue Arabia'', ''Vogue China'', ''Vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inference
Inferences are steps in logical reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle (300s BC). Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction. Various fields study how inference is done in practice. Human inference (i.e. how humans draw conclusions) is traditionally studied within the fields of logic, argumentation studies, and cognitive psychology; artificial intelligence researchers develop automated inference systems to emulate human inference. Statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunctive Syllogism
In classical logic, disjunctive syllogism (historically known as ''modus tollendo ponens'' (MTP), Latin for "mode that affirms by denying") is a valid argument form which is a syllogism having a disjunctive statement for one of its premises. An example in English: # I will choose soup or I will choose salad. # I will not choose soup. # Therefore, I will choose salad. Propositional logic In propositional logic, disjunctive syllogism (also known as disjunction elimination and or elimination, or abbreviated ∨E), is a valid rule of inference. If it is known that at least one of two statements is true, and that it is not the former that is true; we can infer that it has to be the latter that is true. Equivalently, if ''P'' is true or ''Q'' is true and ''P'' is false, then ''Q'' is true. The name "disjunctive syllogism" derives from its being a syllogism, a three-step argument, and the use of a logical disjunction (any "or" statement.) For example, "P or Q" is a disjunction, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exclusive Or
Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or logical inequality is a logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ (one is true, one is false). With multiple inputs, XOR is true if and only if the number of true inputs is odd. It gains the name "exclusive or" because the meaning of "or" is ambiguous when both operands are true. XOR ''excludes'' that case. Some informal ways of describing XOR are "one or the other but not both", "either one or the other", and "A or B, but not A and B". It is symbolized by the prefix operator J Translated as and by the infix operators XOR (, , or ), EOR, EXOR, \dot, \overline, \underline, , \oplus, \nleftrightarrow, and \not\equiv. Definition The truth table of A\nleftrightarrow B shows that it outputs true whenever the inputs differ: Equivalences, elimination, and introduction Exclusive disjunction essentially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivocation
In logic, equivocation ("calling two different things by the same name") is an informal fallacy resulting from the use of a particular word or expression in multiple senses within an argument. It is a type of ambiguity that stems from a phrase having two or more distinct meanings, not from the grammar or structure of the sentence. Fallacy of four terms Equivocation in a syllogism (a chain of reasoning) produces a fallacy of four terms (). Below is an example: : Since only man umanis rational. : And no woman is a man ale : Therefore, no woman is rational. The first instance of "man" implies the entire human species, while the second implies just those who are male. Motte-and-bailey fallacy Equivocation can also be used to conflate two positions which share similarities, one modest and easy to defend and one much more controversial. The arguer advances the controversial position, but when challenged, they insist that they are only advancing the more modest position. See ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Fallacy
In logic and philosophical logic, philosophy, a formal fallacy is a pattern of reasoning rendered validity (logic), invalid by a flaw in its logical structure. propositional calculus, Propositional logic, for example, is concerned with the meanings of sentences and the relationships between them. It focuses on the role of logical operators, called propositional connectives, in determining whether a sentence is true. An error in the sequence will result in a deductive argument that is invalid. The argument itself could have true premises, but still have a false logical consequence, conclusion. Thus, a formal fallacy is a fallacy in which deduction goes wrong, and is no longer a logical process. This may not affect the truth of the conclusion, since validity and truth are separate in formal logic. While a logical argument is a ''non sequitur'' if, and only if, it is invalid, the term "non sequitur" typically refers to those types of invalid arguments which do not constitute formal fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous non-classical treatments, motivated by problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |