|
Adiabatic Connection Fluctuation Dissipation Theorem
In density functional theory (DFT) the adiabatic-connection fluctuation-dissipation theorem (ACFD) is an exact formula for the Kohn–Sham correlation energy. A connection between noninteracting electrons and interacting electrons (the adiabatic connection (AC)) is combined with the random density fluctuations of molecular or solid systems (fluctuation-dissipation (FD)). It is used as a tool in theoretical chemistry and quantum chemistry to approximate the electronic energy. The theorem states where f_(r,r')=\frac is the Hartree kernel, \chi_(r,r',\omega) the interacting dynamic response function, \chi_(r,r',\omega) the dynamic Kohn–Sham (KS) response function from time-dependent density functional theory (TDDFT). History The ACFD theorem in its modern form for density functional theory has been discovered independently by many researches such as D. C. Langreth and J. P. Perdew in 1975, 1977 respectively, by J. Harris together with A. Griffin and R. O. Jones in 1974 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
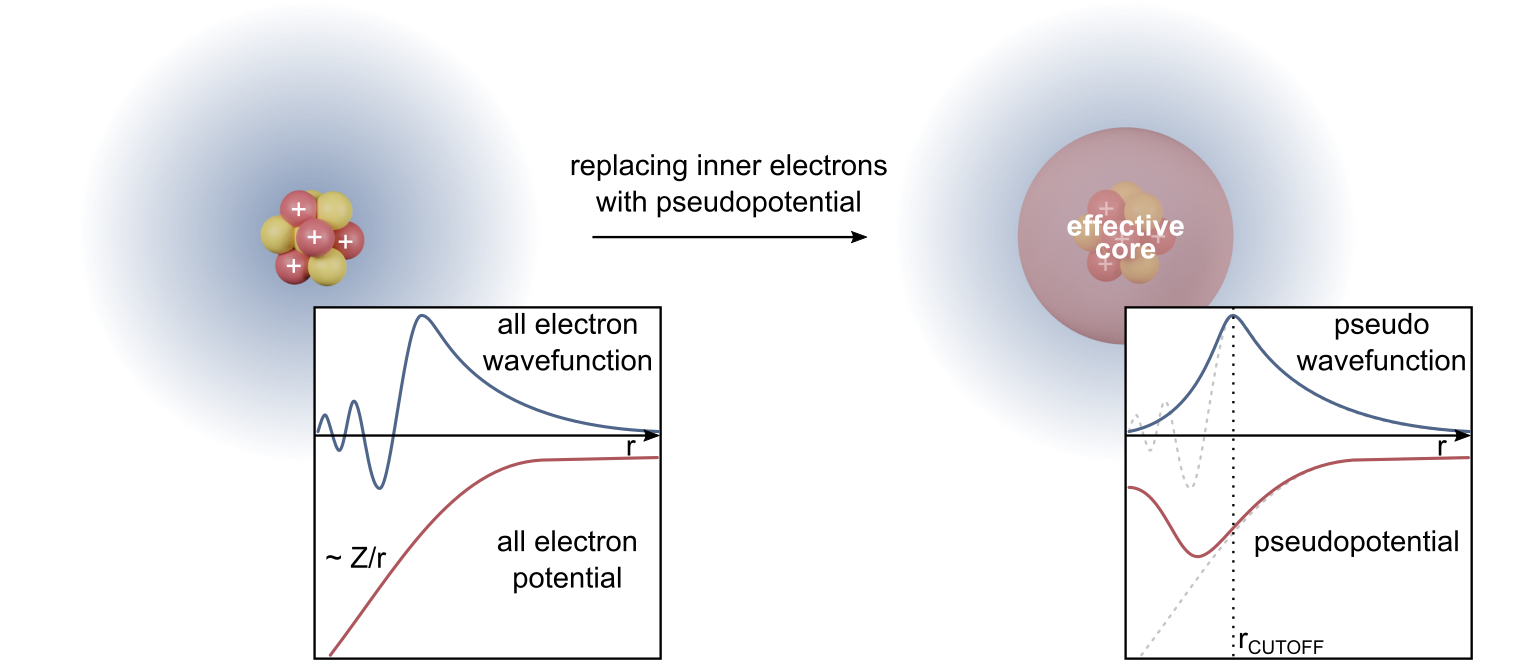
Density Functional Theory
Density functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals - that is, functions that accept a function as input and output a single real number. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990s, when the approximations used in the theory were greatly refined to better m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as Euclidean space. The coordinates are not interchangeable; they are commonly distinguished by their position in an ordered tuple, or by a label, such as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line (geometry), line with real numbers using the ''number line''. In this system, an arbitrary point ''O'' (the ''ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Basis Set (chemistry)
In theoretical chemistry, theoretical and computational chemistry, a basis set is a set of Function (mathematics), functions (called basis functions) that is used to represent the Wave function, electronic wave function in the Hartree–Fock method or Density functional theory, density-functional theory in order to turn the partial differential equations of the model into algebraic equations suitable for efficient implementation on a computer. The use of basis sets is equivalent to the use of an approximate resolution of the identity: the Atomic orbital, orbitals , \psi_i\rangle are expanded within the basis set as a linear combination of the basis functions , \psi_i\rangle \approx \sum_\mu c_ , \mu\rangle, where the expansion coefficients c_ are given by c_ = \sum_\nu \langle \mu, \nu \rangle^ \langle \nu , \psi_i \rangle. The basis set can either be composed of atomic orbitals (yielding the linear combination of atomic orbitals approach), which is the usual choice within the qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
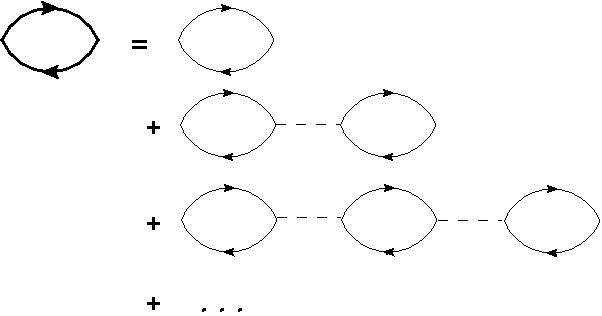
Random Phase Approximation
The random phase approximation (RPA) is an approximation method in condensed matter physics and nuclear physics. It was first introduced by David Bohm and David Pines as an important result in a series of seminal papers of 1952 and 1953. For decades physicists had been trying to incorporate the effect of microscopic quantum mechanical interactions between electrons in the theory of matter. Bohm and Pines' RPA accounts for the weak screened Coulomb interaction and is commonly used for describing the dynamic linear electronic response of electron systems. It was further developed to the relativistic form (RRPA) by solving the Dirac equation. In the RPA, electrons are assumed to respond only to the total electric potential ''V''(r) which is the sum of the external perturbing potential ''V''ext(r) and a screening potential ''V''sc(r). The external perturbing potential is assumed to oscillate at a single frequency ''ω'', so that the model yields via a self-consistent field (SCF) method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dirac Delta Functions
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limits or, as is common in mathematics, measure theory and the theory of distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1. The mathematical rigor of the delta function was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physical Review
''Physical Review'' is a peer-reviewed scientific journal. The journal was established in 1893 by Edward Nichols. It publishes original research as well as scientific and literature reviews on all aspects of physics. It is published by the American Physical Society (APS). The journal is in its third series, and is split in several sub-journals each covering a particular field of physics. It has a sister journal, '' Physical Review Letters'', which publishes shorter articles of broader interest. History ''Physical Review'' commenced publication in July 1893, organized by Cornell University professor Edward Nichols and helped by the new president of Cornell, J. Gould Schurman. The journal was managed and edited at Cornell in upstate New York from 1893 to 1913 by Nichols, Ernest Merritt, and Frederick Bedell. The 33 volumes published during this time constitute ''Physical Review Series I''. The American Physical Society (APS), founded in 1899, took over its publicati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Theodore A
Theodore may refer to: Places * Theodore, Australian Capital Territory, Australia * Theodore, Queensland, Australia * Theodore, Saskatchewan, Canada * Theodore, Alabama, United States * Theodore Reservoir, in Saskatchewan People * Theodore (given name), including a list of people with the name ** Theodore Roosevelt, 26th President of the United States **Grand Wizzard Theodore, American musician and DJ * Theodore (surname), including a list of people with the name Fictional characters * T-Bag (''Prison Break'') (Theodore Bagwell), in ''Prison Break'' * T-Dog (''The Walking Dead'') (Theodore Douglas), in ''The Walking Dead'' * Theodore Huxtable, in ''The Cosby Show'' * Theodore, in ''Alvin and the Chipmunks'' * Theodore Grambell, or CatNap, in video game ''Poppy Playtime'' * Theodore "The Roach" Roachmont, from Supernoobs Other uses * Theodore (horse), a British Thoroughbred racehorse * Theodore Racing, a Formula One constructor See also * Theodoros, or Theodorus * Principa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Herbert Callen
Herbert Bernard Callen (July 1, 1919 – May 22, 1993) was an American physicist specializing in thermodynamics and statistical mechanics. He is considered one of the founders of the modern theory of irreversible thermodynamics, and is the author of the classic textbook '' Thermodynamics and an Introduction to Thermostatistics'', published in two editions. During World War II, his services were invoked in the theoretical division of the Manhattan Project. Life and work A native of Philadelphia, Herbert Callen received his Bachelor of Science degree from Temple University. His graduate studies were interrupted by the Manhattan Project. He also worked on a U.S. Navy project concerning guided missiles (Project Bumblebee) at Princeton University in 1945. Callen subsequently completed his PhD in physics at the Massachusetts Institute of Technology (MIT) in 1947. He was supervised by the physicist László Tisza. His doctoral dissertation concerns the Kelvin thermoelectric and therm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |