|
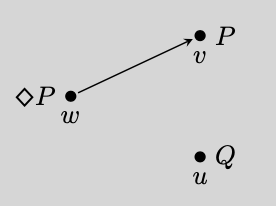
Accessibility Relation
An accessibility relation is a relation (math), relation which plays a key role in assigning truth values to sentences in the Kripke semantics, relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what is true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language linguistic modality, modal statements depend on some, but not all, alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it is raining. Rather, its truth depends on whether such a scenario is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Simple Kripke Model
Simple or SIMPLE may refer to: *Simplicity, the state or quality of being simple Arts and entertainment * ''Simple'' (album), by Andy Yorke, 2008, and its title track * "Simple" (Florida Georgia Line song), 2018 * "Simple", a song by Johnny Mathis from the 1984 album ''A Special Part of Me'' * "Simple", a song by Collective Soul from the 1995 album ''Collective Soul'' * "Simple", a song by Katy Perry from the 2005 soundtrack to ''The Sisterhood of the Traveling Pants'' * "Simple", a song by Khalil from the 2017 album ''Prove It All'' * "Simple", a song by Kreesha Turner from the 2008 album ''Passion'' * "Simple", a song by Ty Dolla Sign from the 2017 album ''Beach House 3'' deluxe version * ''Simple'' (video game series), budget-priced console games Businesses and organisations * Simple (bank), an American direct bank * SIMPLE Group, a consulting conglomeration based in Gibraltar * Simple Shoes, an American footwear brand * Simple Skincare, a British brand of soap an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Relation (math)
In mathematics, a relation denotes some kind of ''relationship'' between two objects in a set, which may or may not hold. As an example, "''is less than''" is a relation on the set of natural numbers; it holds, for instance, between the values and (denoted as ), and likewise between and (denoted as ), but not between the values and nor between and , that is, and both evaluate to false. As another example, "''is sister of'' is a relation on the set of all people, it holds e.g. between Marie Curie and Bronisława Dłuska, and likewise vice versa. Set members may not be in relation "to a certain degree" – either they are in relation or they are not. Formally, a relation over a set can be seen as a set of ordered pairs of members of . The relation holds between and if is a member of . For example, the relation "''is less than''" on the natural numbers is an infinite set of pairs of natural numbers that contains both and , but neither nor . The relation "''is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kripke Semantics
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so: \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modal Logic
Modal logic is a kind of logic used to represent statements about Modality (natural language), necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causality, causation. For instance, in epistemic modal logic, the well-formed_formula, formula \Box P can be used to represent the statement that P is known. In deontic modal logic, that same formula can represent that P is a moral obligation. Modal logic considers the inferences that modal statements give rise to. For instance, most epistemic modal logics treat the formula \Box P \rightarrow P as a Tautology_(logic), tautology, representing the principle that only true statements can count as knowledge. However, this formula is not a tautology in deontic modal logic, since what ought to be true can be false. Modal logics are formal systems that include unary operation, unary operators such as \Diamond and \Box, representing possibility and necessi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Possible World
A possible world is a complete and consistent way the world is or could have been. Possible worlds are widely used as a formal device in logic, philosophy, and linguistics in order to provide a semantics for intensional and modal logic. Their metaphysical status has been a subject of controversy in philosophy, with modal realists such as David Lewis arguing that they are literally existing alternate realities, and others such as Robert Stalnaker arguing that they are not. Logic Possible worlds are one of the foundational concepts in modal and intensional logics. Formulas in these logics are used to represent statements about what ''might'' be true, what ''should'' be true, what one ''believes'' to be true and so forth. To give these statements a formal interpretation, logicians use structures containing possible worlds. For instance, in the relational semantics for classical propositional modal logic, the formula \Diamond P (read as "possibly P") is actually true if and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Natural Language
A natural language or ordinary language is a language that occurs naturally in a human community by a process of use, repetition, and change. It can take different forms, typically either a spoken language or a sign language. Natural languages are distinguished from constructed and formal languages such as those used to program computers or to study logic. Defining natural language Natural languages include ones that are associated with linguistic prescriptivism or language regulation. ( Nonstandard dialects can be viewed as a wild type in comparison with standard languages.) An official language with a regulating academy such as Standard French, overseen by the , is classified as a natural language (e.g. in the field of natural language processing), as its prescriptive aspects do not make it constructed enough to be a constructed language or controlled enough to be a controlled natural language. Natural language are different from: * artificial and constructed la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linguistic Modality
In linguistics and philosophy, modality refers to the ways language can express various relationships to reality or truth. For instance, a modal expression may convey that something is likely, desirable, or permissible. Quintessential modal expressions include modal auxiliaries such as "could", "should", or "must"; modal adverbs such as "possibly" or "necessarily"; and modal adjectives such as "conceivable" or "probable". However, modal components have been identified in the meanings of countless natural language expressions, including counterfactuals, propositional attitudes, evidentials, habituals, and generics. Modality has been intensely studied from a variety of perspectives. Within linguistics, typological studies have traced crosslinguistic variation in the strategies used to mark modality, with a particular focus on its interaction with tense–aspect–mood marking. Theoretical linguists have sought to analyze both the propositional content and discourse effect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Epistemic Logic
Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy, theoretical computer science, artificial intelligence, economics, and linguistics. While philosophers since Aristotle have discussed modal logic, and Medieval philosophers such as Avicenna, Ockham, and Duns Scotus developed many of their observations, it was C. I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Saul Kripke. Historical development Many papers were written in the 1950s that spoke of a logic of knowledge in passing, but the Finnish philosopher G. H. von Wright's 1951 paper titled ''An Essay in Modal Logic'' is seen as a founding document. It was not unti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Deontic Logic
Deontic logic is the field of philosophical logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. It can be used to formalize imperative logic, or directive modality in natural languages. Typically, a deontic logic uses ''OA'' to mean ''it is obligatory that A'' (or ''it ought to be (the case) that A''), and ''PA'' to mean ''it is permitted (or permissible) that A'', which is defined as PA\equiv \neg O\neg A. In natural language, the statement "You may go to the zoo OR the park" should be understood as Pz\land Pp instead of Pz\lor Pp, as both options are permitted by the statement. When there are multiple agents involved in the domain of discourse, the deontic modal operator can be specified to each agent to express their individual obligations and permissions. For example, by using a subscript O_i for agent a_i, O_iA means that "It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kripke Structure (model Checking)
A Kripke structure is a variation of the transition system, originally proposed by Saul Kripke, used in model checking to represent the behavior of a system. It consists of a graph whose nodes represent the reachable states of the system and whose edges represent state transitions, together with a labelling function which maps each node to a set of properties that hold in the corresponding state. Temporal logics are traditionally interpreted in terms of Kripke structures. Formal definition Let be a set of ''atomic propositions'', i.e. boolean-valued expressions formed from variables, constants and predicate symbols. Clarke et al. define a Kripke structure over as a 4-tuple consisting of * a finite set of states . * a set of initial states . * a transition relation such that is left-total, i.e., such that . * a labeling (or ''interpretation'') function . Since is left-total, it is always possible to construct an infinite path through the Kripke structure. A deadlock state ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Propositional Attitude
A propositional attitude is a mental state held by an agent or organism toward a proposition. In philosophy, propositional attitudes can be considered to be neurally realized, causally efficacious, content-bearing internal states (personal principles/values). Linguistically, propositional attitudes are denoted by a verb (e.g. ''believed'') governing an embedded "that" clause, for example, 'Sally believed that she had won'. Propositional attitudes are often assumed to be the fundamental units of thought and their contents, being propositions, are true or false from the perspective of the person. An agent can have different propositional attitudes toward the same proposition (e.g., "''S'' believes that her ice-cream is cold," and "''S'' fears that her ice-cream is cold"). Propositional attitudes have directions of fit: some are meant to reflect the world, others to influence it. One topic of central concern is the relation between the modalities of assertion and belief, as well as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modal Depth
In modal logic, the modal depth of a formula is the deepest nesting of modal operators (commonly \Box and \Diamond). Modal formulas without modal operators have a modal depth of zero. Definition Modal depth can be defined as follows. Let \operatorname(\phi) be a function that computes the modal depth for a modal formula \phi: :\operatorname(p) = 0, where p is an atomic formula. :\operatorname(\top) = 0 :\operatorname(\bot) = 0 :\operatorname(\neg \varphi) = \operatorname(\varphi) :\operatorname(\varphi \wedge \psi) = \max(\operatorname(\varphi), \operatorname(\psi)) :\operatorname(\varphi \vee \psi) = \max(\operatorname(\varphi), \operatorname(\psi)) :\operatorname(\varphi \rightarrow \psi) = \max(\operatorname(\varphi), \operatorname(\psi)) :\operatorname(\Box \varphi) = 1 + \operatorname(\varphi) :\operatorname(\Diamond \varphi) = 1 + \operatorname(\varphi) Example The following computation gives the modal depth of \Box ( \Box p \rightarrow p ): :\operatorname(\Box ( \Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |