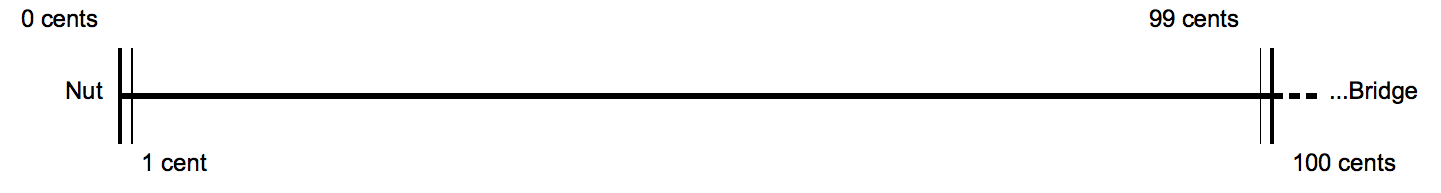|
Young Temperament
"Young temperament" may refer to either of a pair of circulating temperaments described by Thomas Young in a letter dated July 9, 1799, to the Royal Society of London. The letter was read at the Society's meeting of January 16, 1800, and included in its ''Philosophical Transactions'' for that year. The temperaments are referred to individually as "Young's first temperament" and "Young's second temperament", more briefly as "Young's No. 1" and "Young's No. 2", or with some other variations of these expressions. Young argued that there were good reasons for choosing a temperament to make "the harmony most perfect in those keys which are the most frequently used", and presented his first temperament as a way of achieving this. He gave his second temperament as a method of "very simply" producing "nearly the same effect". First temperament In his first temperament, Young chose to make the major third C-E wider than just by of a syntonic comma (about 5 cents, ), and the major ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well Temperament
Well temperament (also good temperament, circular or circulating temperament) is a type of tempered tuning described in 20th-century music theory. The term is modeled on the German word ''wohltemperiert''. This word also appears in the title of J. S. Bach's famous composition "Das wohltemperierte Klavier", ''The Well-Tempered Clavier''. Origins As used in the 17th century, the term "well tempered" meant that the twelve notes per octave of the standard keyboard were tuned in such a way that it was possible to play music in all major or minor keys that were commonly in use, without sounding perceptibly out of tune. One of the first attestations of the concept of "well tempered" is found in a treatise in German by the music theorist Andreas Werckmeister. In the subtitle of his ''Orgelprobe'', from 1681, he writes: The words and were subsequently combined into . A modern definition of "well temperament", from Herbert Kelletat, is given below: : In most tuning systems use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vallotti Temperament
Vallotti temperament (or simply Vallotti, Vallotti-Barca, or Vallotti-Tartini) is a slightly modified version of a circulating temperament devised by the 18th-century organist, composer, and music theorist, Francesco Vallotti. Vallotti's description of his temperament appears in book 2 of his treatise, ''Della scienza teorica e pratica della moderna musica'' (''On the theoretical and practical science of modern music''). Although Vallotti stated that he had developed his theoretical system—presumably including the details of his temperament—by 1728, the first book of his treatise was not published until 1779, the year before he died. At the time of his death, the other three books had not been published, and remained only in manuscript form until an edition of all four books was published in 1950, under the title ''Trattato della moderna musica'' (''Treatise on modern music''). Vallotti's temperament received very little attention during his lifetime and for some time there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditonic Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as the differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal Temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, which gives an equal perceived step size as pitch is perceived roughly as the logarithm of frequency. In classical music and Western music in general, the most common tuning system since the 18th century has been twelve-tone equal temperament (also known as 12 equal temperament, 12-TET or 12-ET; informally abbreviated to twelve equal), which divides the octave into 12 parts, all of which are equal on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. In Western countries the term ''equal temperament'', without qualification, generally means 12-TET. In modern times, 12-TET is usually tuned relative to a standard pit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval of diminished sixth to be treated as a fifth). If C is chosen as a starting point, the sequence is: C, G, D, A, E, B (=C), F (=G), C (=D), A, E, B, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle. Definition The circle of fifths organizes pitches in a sequence of perfect fifths, generally shown as a circle with the pitches (and their corresponding keys) in a clockwise progression. Musicians and composers often use the circle of fifths to describe the musical relationships between pitches. Its design is helpful in composing and harmonizing melodies, building chords, and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
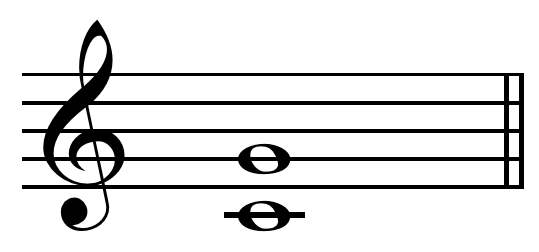
Perfect Fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note. The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, , at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed, and further described and employed the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard method of representi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios (such as 3:2 or 4:3) of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth. In Western musical practice, instruments are rarely tuned using only pure intervals—the desire for different keys to have identical intervals in Western music makes this impractical. Some instruments of fixed pitch, such as electric pianos, are commonly tuned using equal temperament, in which all intervals other than octaves consist of irrational-number freque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |