|
Weyl Algebra
In abstract algebra, the Weyl algebras are abstracted from the ring of differential operators with polynomial coefficients. They are named after Hermann Weyl, who introduced them to study the Heisenberg uncertainty principle in quantum mechanics. In the simplest case, these are differential operators. Let F be a field, and let F /math> be the ring of polynomials in one variable with coefficients in F. Then the corresponding Weyl algebra consists of differential operators of form : f_m(x) \partial_x^m + f_(x) \partial_x^ + \cdots + f_1(x) \partial_x + f_0(x) This is the first Weyl algebra A_1. The ''n''-th Weyl algebra A_n are constructed similarly. Alternatively, A_1 can be constructed as the quotient of the free algebra on two generators, ''q'' and ''p'', by the ideal generated by ( ,q- 1). Similarly, A_n is obtained by quotienting the free algebra on ''2n'' generators by the ideal generated by ( _i,q_j- \delta_), \quad \forall i, j = 1, \dots, nwhere \delta_ is the K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structures include group (mathematics), groups, ring (mathematics), rings, field (mathematics), fields, module (mathematics), modules, vector spaces, lattice (order), lattices, and algebra over a field, algebras over a field. The term ''abstract algebra'' was coined in the early 20th century to distinguish it from older parts of algebra, and more specifically from elementary algebra, the use of variable (mathematics), variables to represent numbers in computation and reasoning. The abstract perspective on algebra has become so fundamental to advanced mathematics that it is simply called "algebra", while the term "abstract algebra" is seldom used except in mathematical education, pedagogy. Algebraic structures, with their associated homomorphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Ring
In abstract algebra, a matrix ring is a set of matrices with entries in a ring ''R'' that form a ring under matrix addition and matrix multiplication. The set of all matrices with entries in ''R'' is a matrix ring denoted M''n''(''R'') (alternative notations: Mat''n''(''R'') and ). Some sets of infinite matrices form infinite matrix rings. A subring of a matrix ring is again a matrix ring. Over a rng, one can form matrix rngs. When ''R'' is a commutative ring, the matrix ring M''n''(''R'') is an associative algebra over ''R'', and may be called a matrix algebra. In this setting, if ''M'' is a matrix and ''r'' is in ''R'', then the matrix ''rM'' is the matrix ''M'' with each of its entries multiplied by ''r''. Examples * The set of all square matrices over ''R'', denoted M''n''(''R''). This is sometimes called the "full ring of ''n''-by-''n'' matrices". * The set of all upper triangular matrices over ''R''. * The set of all lower triangular matrices over ''R''. * The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925. It was the first conceptually autonomous and logically consistent formulation of quantum mechanics. Its account of quantum jumps supplanted the Bohr model's electron orbits. It did so by interpreting the physical properties of particles as matrices that evolve in time. It is equivalent to the Schrödinger wave formulation of quantum mechanics, as manifest in Dirac's bra–ket notation. In some contrast to the wave formulation, it produces spectra of (mostly energy) operators by purely algebraic, ladder operator methods. Relying on these methods, Wolfgang Pauli derived the hydrogen atom spectrum in 1926, before the development of wave mechanics. Development of matrix mechanics In 1925, Werner Heisenberg, Max Born, and Pascual Jordan formulated the matrix mechanics representation of quantum mechanics. Epiphany at Helgoland In 1925 Werner Heisenberg w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra Representation
In abstract algebra, a representation of an associative algebra is a module for that algebra. Here an associative algebra is a (not necessarily unital) ring. If the algebra is not unital, it may be made so in a standard way (see the adjoint functors page); there is no essential difference between modules for the resulting unital ring, in which the identity acts by the identity mapping, and representations of the algebra. Examples Linear complex structure One of the simplest non-trivial examples is a linear complex structure, which is a representation of the complex numbers C, thought of as an associative algebra over the real numbers R. This algebra is realized concretely as \mathbb = \mathbb (x^2+1), which corresponds to . Then a representation of C is a real vector space ''V'', together with an action of C on ''V'' (a map \mathbb \to \mathrm(V)). Concretely, this is just an action of , as this generates the algebra, and the operator representing (the image of in End('' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger ( ; ; 12 August 1887 – 4 January 1961), sometimes written as or , was an Austrian-Irish theoretical physicist who developed fundamental results in quantum field theory, quantum theory. In particular, he is recognized for postulating the Schrödinger equation, an equation that provides a way to calculate the wave function of a system and how it changes dynamically in time. Schrödinger coined the term "quantum entanglement" in 1935. In addition, he wrote many works on various aspects of physics: statistical mechanics and thermodynamics, physics of dielectrics, color theory, electrodynamics, general relativity, and cosmology, and he made several attempts to construct a unified field theory. In his book ''What Is Life?'' Schrödinger addressed the problems of genetics, looking at the phenomenon of life from the point of view of physics. He also paid great attention to the philosophical aspects of science, ancient, and oriental philoso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory. Group theory The commutator of two elements, and , of a group , is the element : . This element is equal to the group's identity if and only if and commute (that is, if and only if ). The set of all commutators of a group is not in general closed under the group operation, but the subgroup of ''G'' generated by all commutators is closed and is called the ''derived group'' or the '' commutator subgroup'' of ''G''. Commutators are used to define nilpotent and solvable groups and the largest abelian quotient group. The definition of the commutator above is used throughout this article, but many group theorists define the commutator as : . Using the first definition, this can be expressed as . Identities (group theory) Commutator identities are an important tool in group th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-adjoint Operator
In mathematics, a self-adjoint operator on a complex vector space ''V'' with inner product \langle\cdot,\cdot\rangle is a linear map ''A'' (from ''V'' to itself) that is its own adjoint. That is, \langle Ax,y \rangle = \langle x,Ay \rangle for all x, y ∊ ''V''. If ''V'' is finite-dimensional with a given orthonormal basis, this is equivalent to the condition that the matrix of ''A'' is a Hermitian matrix, i.e., equal to its conjugate transpose ''A''. By the finite-dimensional spectral theorem, ''V'' has an orthonormal basis such that the matrix of ''A'' relative to this basis is a diagonal matrix with entries in the real numbers. This article deals with applying generalizations of this concept to operators on Hilbert spaces of arbitrary dimension. Self-adjoint operators are used in functional analysis and quantum mechanics. In quantum mechanics their importance lies in the Dirac–von Neumann formulation of quantum mechanics, in which physical observables such as position, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called '' canonical transformations'', which map canonical coordinate systems into other canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables (below symbolized by q_i and p_i, respectively) that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself \mathcal H =\mathcal H(q, p, t) as one of the new canonical momentum coordinates. In a more general sense, the Poisson bracket is used to define a Poisson algebra, of which the algebra of functions on a Poisson manifold is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
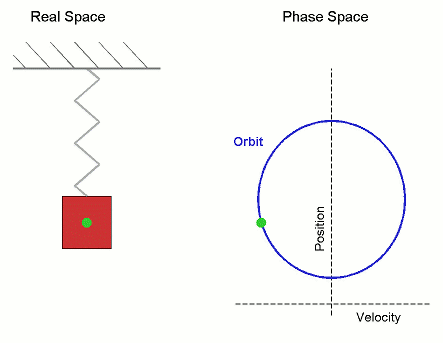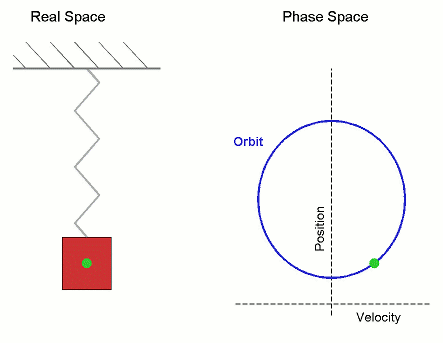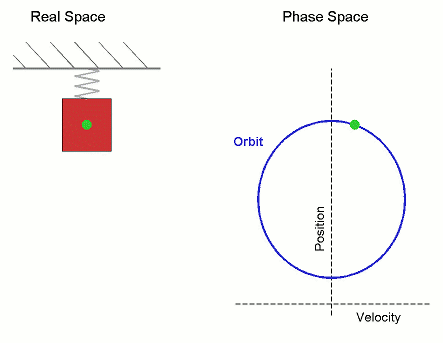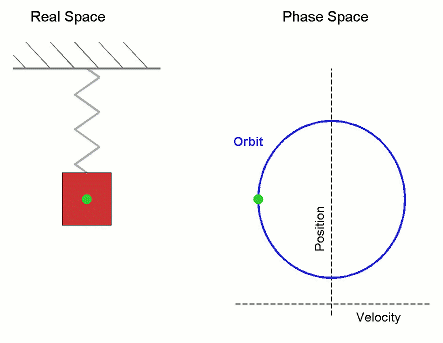
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Quantization
In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory to the greatest extent possible. Historically, this was not quite Werner Heisenberg's route to obtaining quantum mechanics, but Paul Dirac introduced it in his 1926 doctoral thesis, the "method of classical analogy" for quantization, and detailed it in his classic text ''Principles of Quantum Mechanics''. The word ''canonical'' arises from the Hamiltonian approach to classical mechanics, in which a system's dynamics is generated via canonical Poisson brackets, a structure which is ''only partially preserved'' in canonical quantization. This method was further used by Paul Dirac in the context of quantum field theory, in his construction of quantum electrodynamics. In the field theory context, it is also called the second quantization of fields, in contrast to the semi-classical first quantizati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |