|
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
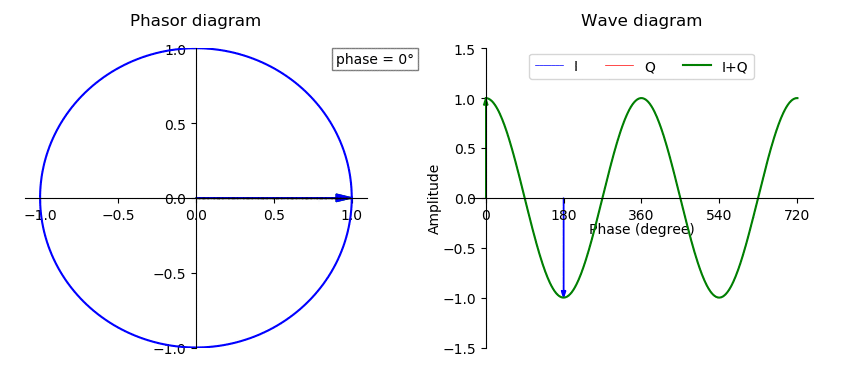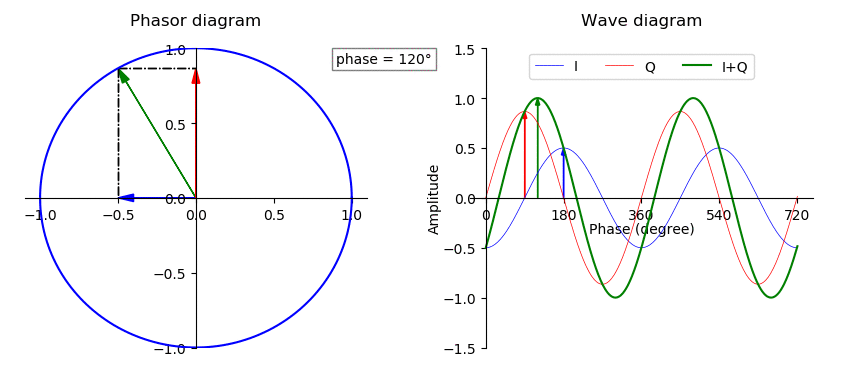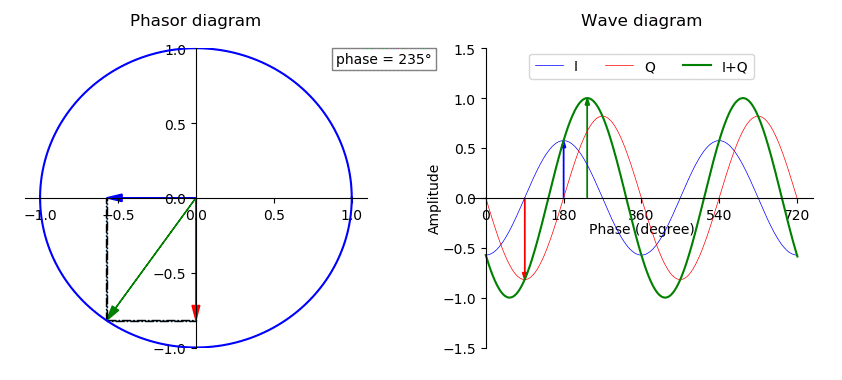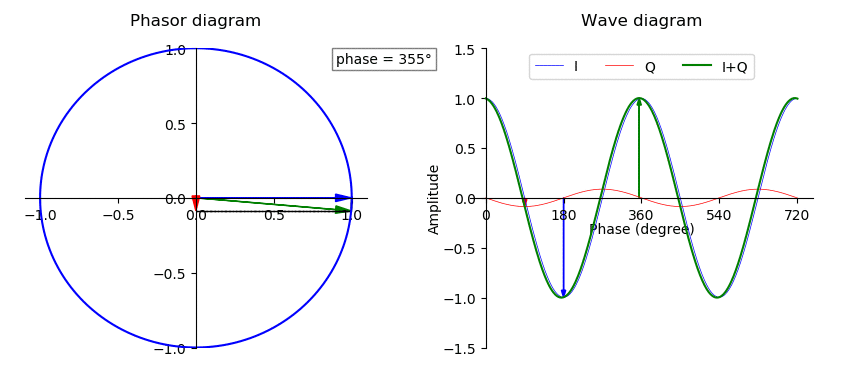
Phase Offset
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glass
Glass is an amorphous (non-crystalline solid, non-crystalline) solid. Because it is often transparency and translucency, transparent and chemically inert, glass has found widespread practical, technological, and decorative use in window panes, tableware, and optics. Some common objects made of glass are named after the material, e.g., a Tumbler (glass), "glass" for drinking, "glasses" for vision correction, and a "magnifying glass". Glass is most often formed by rapid cooling (quenching) of the Melting, molten form. Some glasses such as volcanic glass are naturally occurring, and obsidian has been used to make arrowheads and knives since the Stone Age. Archaeological evidence suggests glassmaking dates back to at least 3600 BC in Mesopotamia, Ancient Egypt, Egypt, or Syria. The earliest known glass objects were beads, perhaps created accidentally during metalworking or the production of faience, which is a form of pottery using lead glazes. Due to its ease of formability int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amorphous Solids
In condensed matter physics and materials science, an amorphous solid (or non-crystalline solid) is a solid that lacks the long-range order that is a characteristic of a crystal. The terms "glass" and "glassy solid" are sometimes used synonymously with amorphous solid; however, these terms refer specifically to amorphous materials that undergo a glass transition. Examples of amorphous solids include glasses, metallic glasses, and certain types of plastics and polymers. Etymology The term "Amorphous" comes from the Greek ''a'' ("without"), and ''morphé'' ("shape, form"). Structure Amorphous materials have an internal structure of molecular-scale structural blocks that can be similar to the basic structural units in the crystalline phase of the same compound. Unlike in crystalline materials, however, no long-range regularity exists: amorphous materials cannot be described by the repetition of a finite unit cell. Statistical measures, such as the atomic density function an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Attenuation
In physics, attenuation (in some contexts, extinction) is the gradual loss of flux intensity through a Transmission medium, medium. For instance, dark glasses attenuate sunlight, lead attenuates X-rays, and water and air attenuate both light and sound at variable attenuation rates. Hearing protection device, Hearing protectors help reduce Sound power, acoustic flux from flowing into the ears. This phenomenon is called acoustic attenuation and is measured in decibels (dBs). In electrical engineering and telecommunications, attenuation affects the Wave propagation, propagation of waves and signals in electrical circuits, in optical fibers, and in air. Attenuator (electronics), Electrical attenuators and optical attenuators are commonly manufactured components in this field. Background In many cases, attenuation is an exponential function of the path length through the medium. In optics and in chemical spectroscopy, this is known as the Beer–Lambert law. In engineering, attenu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
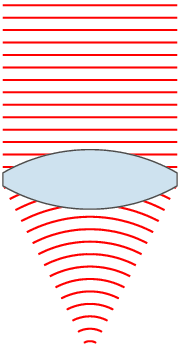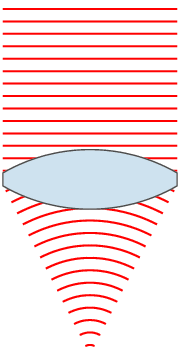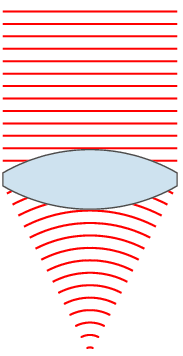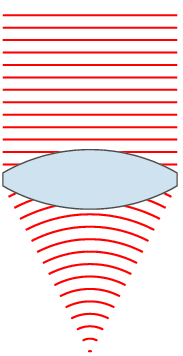
Wavefronts
In physics, the wavefront of a time-varying ''wave field'' is the set ( locus) of all points having the same ''phase''. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined). Wavefronts usually move with time. For waves propagating in a unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surfaces in a three-dimensional one. For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefronts may change by refraction. In particular, lenses can change the shape of optical wavefronts from planar to sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Front
In physics, the wavefront of a time-varying ''wave field'' is the set ( locus) of all points having the same '' phase''. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined). Wavefronts usually move with time. For waves propagating in a unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surfaces in a three-dimensional one. For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefronts may change by refraction. In particular, lenses can change the shape of optical wavefronts from planar to s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Normal
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the curve at the point. A normal vector is a vector perpendicular to a given object at a particular point. A normal vector of length one is called a unit normal vector or normal direction. A curvature vector is a normal vector whose length is the curvature of the object. Multiplying a normal vector by results in the opposite vector, which may be used for indicating sides (e.g., interior or exterior). In three-dimensional space, a surface normal, or simply normal, to a surface at point is a vector perpendicular to the tangent plane of the surface at . The vector field of normal directions to a surface is known as '' Gauss map''. The word "normal" is also used as an adjective: a line ''normal'' to a plane, the ''normal'' component of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength (lambda) and time period as :v_\mathrm = \frac. Equivalently, in terms of the wave's angular frequency , which specifies angular change per unit of time, and wavenumber (or angular wave number) , which represent the angular change per unit of space, :v_\mathrm = \frac. To gain some basic intuition for this equation, we consider a propagating (cosine) wave . We want to see how fast a particular phase of the wave travels. For example, we can choose , the phase of the first crest. This implies , and so . Formally, we let the phase and see immediately that and . So, it immediately follows that : \frac = -\frac \frac = \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poynting Vector
In physics, the Poynting vector (or Umov–Poynting vector) represents the directional energy flux (the energy transfer per unit area, per unit time) or '' power flow'' of an electromagnetic field. The SI unit of the Poynting vector is the watt per square metre (W/m2); kg/s3 in SI base units. It is named after its discoverer John Henry Poynting who first derived it in 1884. Nikolay Umov is also credited with formulating the concept. Oliver Heaviside also discovered it independently in the more general form that recognises the freedom of adding the curl of an arbitrary vector field to the definition. The Poynting vector is used throughout electromagnetics in conjunction with Poynting's theorem, the continuity equation expressing conservation of electromagnetic energy, to calculate the power flow in electromagnetic fields. Definition In Poynting's original paper and in most textbooks, the Poynting vector \mathbf is defined as the cross product \mathbf = \mathbf \time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope (waves), envelope'' of the wave—propagates through space. For example, if a stone is thrown into the middle of a very still pond, a circular pattern of waves with a quiescent center appears in the water, also known as a capillary wave. The expanding ring of waves is the wave group or wave packet, within which one can discern individual waves that travel faster than the group as a whole. The amplitudes of the individual waves grow as they emerge from the trailing edge of the group and diminish as they approach the leading edge of the group. History The idea of a group velocity distinct from a wave's phase velocity was first proposed by William Rowan Hamilton, W.R. Hamilton in 1839, and the first full treatment was by John Strutt, 3rd Baron Rayleigh, Rayleigh in his "Theory of Sound" in 1877. Definition and interpretation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |