|
Trisectrix Of Maclaurin
In algebraic geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the point of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the rates of rotation is 1:3 and the lines initially coincide with the line between the two points. A generalization of this construction is called a sectrix of Maclaurin. The curve is named after Colin Maclaurin who investigated the curve in 1742. Equations Let two lines rotate about the points P = (0,0) and P_1 = (a, 0) so that when the line rotating about P has angle \theta with the ''x'' axis, the rotating about P_1 has angle 3\theta. Let Q be the point of intersection, then the angle formed by the lines at Q is 2\theta. By the law of sines, : = \! so the equation in polar coordinates is (up to translation and rotation) :r= a \frac = \frac = (4 \cos \theta - \sec \theta)\!. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maclaurin Animated2
Maclaurin or MacLaurin is a surname. Notable people with the surname include: * Colin Maclaurin (1698–1746), Scottish mathematician * Normand MacLaurin (1835–1914), Australian politician and university administrator * Henry Normand MacLaurin (1878–1915), Australian general * Ian MacLaurin, Baron MacLaurin of Knebworth * Richard Cockburn Maclaurin (1870–1920), US physicist and educator See also * Taylor series in mathematics, a special case of which is the ''Maclaurin series'' * Maclaurin (crater), a crater on the Moon * McLaurin (other) * MacLaren (surname) * McLaren (other) {{surname, Maclaurin Clan MacLaren ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Folium Of Descartes
In geometry, the folium of Descartes (; named for René Decartes) is an algebraic curve defined by the implicit equation :x^3 + y^3 - 3 a x y = 0. History The curve was first proposed and studied by René Descartes in 1638. Its claim to fame lies in an incident in the development of calculus. Descartes challenged Pierre de Fermat to find the tangent line to the curve at an arbitrary point since Fermat had recently discovered a method for finding tangent lines. Fermat solved the problem easily, something Descartes was unable to do. Since the invention of calculus, the slope of the tangent line can be found easily using implicit differentiation. Graphing the curve The folium of Descartes can be expressed in polar coordinates as :r = \frac, which is plotted on the left. This is equivalent to r = \frac. Another technique is to write y = px and solve for x and y in terms of p. This yields the rational parametric equations: x = ,\, y = . We can see that the parameter is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
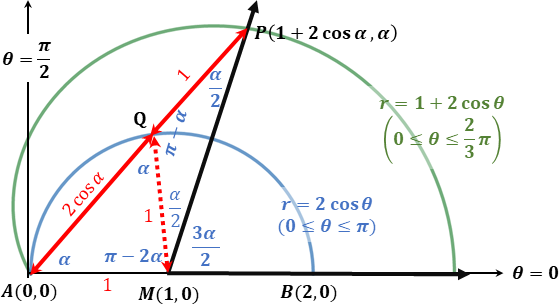
Limaçon Trisectrix
In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose, conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin. Specification and loop structure The limaçon trisectrix specified as a polar equation is :r= a(1+2\cos\theta). The constant a may be positive or negative. The two curves with constants a and -a are reflections of each other across the line \theta=\pi/2. The period of r= a(1+2\cos\theta) is 2\pi given the period of the sinusoid \cos\theta. The limaçon trisectrix is composed of two loops. * The outer loop is defined when 1+2\cos\theta\ge0 on the polar angle interval -2\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pedal Curve
A pedal (from the Latin '' pes'' ''pedis'', "foot") is a lever designed to be operated by foot and may refer to: Computers and other equipment * Footmouse, a foot-operated computer mouse * In medical transcription, a pedal is used to control playback of voice dictations Geometry * Pedal curve, a curve derived by construction from a given curve * Pedal triangle, a triangle obtained by projecting a point onto the sides of a triangle Music Albums * ''Pedals'' (Rival Schools album) * ''Pedals'' (Speak album) Other music * Bass drum pedal, a pedal used to play a bass drum while leaving the drummer's hands free to play other drums with drum sticks, hands, etc. * Effects pedal, a pedal used commonly for electric guitars * Pedal keyboard, a musical keyboard operated by the player's feet * Pedal harp, a modern orchestral harp with pedals used to change the tuning of its strings * Pedal point, a type of nonchord tone, usually in the bass * Pedal tone, a fundamental tone pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cissoid
In geometry, a cissoid (() is a plane curve generated from two given curves , and a point (the pole). Let be a variable line passing through and intersecting at and at . Let be the point on so that \overline = \overline. (There are actually two such points but is chosen so that is in the same direction from as is from .) Then the locus of such points is defined to be the cissoid of the curves , relative to . Slightly different but essentially equivalent definitions are used by different authors. For example, may be defined to be the point so that \overline = \overline + \overline. This is equivalent to the other definition if is replaced by its reflection through . Or may be defined as the midpoint of and ; this produces the curve generated by the previous curve scaled by a factor of 1/2. Equations If and are given in polar coordinates by r=f_1(\theta) and r=f_2(\theta) respectively, then the equation r=f_2(\theta)-f_1(\theta) describes the cissoid of and r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Curve
In inversive geometry, an inverse curve of a given curve is the result of applying an inverse operation to . Specifically, with respect to a fixed circle with center and radius the inverse of a point is the point for which lies on the ray and . The inverse of the curve is then the locus of as runs over . The point in this construction is called the center of inversion, the circle the circle of inversion, and the radius of inversion. An inversion applied twice is the identity transformation, so the inverse of an inverse curve with respect to the same circle is the original curve. Points on the circle of inversion are fixed by the inversion, so its inverse is itself. Equations The inverse of the point with respect to the unit circle is where :X = \frac,\qquad Y=\frac, or equivalently :x = \frac,\qquad y=\frac. So the inverse of the curve determined by with respect to the unit circle is :f\left(\frac, \frac\right)=0. It is clear from this that inverting an alge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Point
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied. Algebraic curves in the plane Algebraic curves in the plane may be defined as the set of points satisfying an equation of the form f(x,y) = 0, where is a polynomial function If is expanded as f = a_0 + b_0 x + b_1 y + c_0 x^2 + 2c_1 xy + c_2 y^2 + \cdots If the origin is on the curve then . If then the implicit function theorem guarantees there is a smooth function so that the curve has the form near the origin. Similarly, if then there is a smooth function so that the curve has the form near the origin. In either case, there is a smooth map from to the plane which defines the curve in the neighborhood of the origin. Note that at the origin b_0 = \frac, \; b_1 = \frac, so the curve is non-singular or ''regular'' at the origin if at least one of the partial derivatives o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |