|
Thin-film Equation
In fluid mechanics, the thin-film equation is a partial differential equation that approximately predicts the time evolution of the thickness of a liquid film that lies on a surface. The equation is derived via lubrication theory which is based on the assumption that the length-scales in the surface directions are significantly larger than in the direction Normal (geometry), normal to the surface. In the non-dimensional form of the Navier–Stokes equations, Navier-Stokes equation the requirement is that terms of order and are negligible, where is the aspect ratio and is the Reynolds number. This significantly simplifies the governing equations. However, lubrication theory, as the name suggests, is typically derived for flow between two solid surfaces, hence the liquid forms a lubricating layer. The thin-film equation holds when there is a single free surface. With two free surfaces, the flow must be treated as a viscous sheet. Definition The basic form of a 2-dimensional t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasma (physics), plasmas) and the forces on them. Originally applied to water (hydromechanics), it found applications in a wide range of disciplines, including mechanical engineering, mechanical, aerospace engineering, aerospace, civil engineering, civil, chemical engineering, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology. It can be divided into ''fluid statics'', the study of various fluids at rest; and ''fluid dynamics'', the study of the effect of forces on fluid motion. It is a branch of ''continuum mechanics'', a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
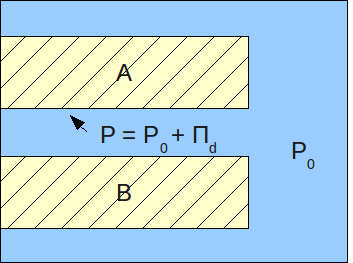
Disjoining Pressure
In surface chemistry, disjoining pressure (symbol ) according to an IUPAC definition arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure (i.e., the force per unit area) can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance (in the direction normal to that of the interacting surfaces). There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces. The concept of disjoining pressure was introduced by Derjaguin (1936) as the difference between the pressure in a region of a phase adjacent to a surface confining it, and the pressure in the bulk of this phase. Description Disjoining pressure can be expressed as:Hans-Jürgen Butt, Karlheinz Graf, Michael Kappl,"Physics and chemistry of interfaces", John Wiley & Sons Canada, Ltd., 1 edition, 2003, page 9(Google books)/ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lubrication Theory
In fluid dynamics, lubrication theory describes the flow of fluids (liquids or gases) in a geometry in which one dimension is significantly smaller than the others. An example is the flow above air hockey tables, where the thickness of the air layer beneath the puck is much smaller than the dimensions of the puck itself. Internal flows are those where the fluid is fully bounded. Internal flow lubrication theory has many industrial applications because of its role in the design of fluid bearings. Here a key goal of lubrication theory is to determine the pressure distribution in the fluid volume, and hence the forces on the bearing components. The working fluid in this case is often termed a lubricant. Free film lubrication theory is concerned with the case in which one of the surfaces containing the fluid is a free surface. In that case, the position of the free surface is itself unknown, and one goal of lubrication theory is then to determine this. Examples include the flow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Washburn's Equation
In physics, Washburn's equation describes capillary flow in a bundle of parallel cylindrical tubes; it is extended with some issues also to imbibition into porous Porosity or void fraction is a measure of the void (i.e. "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure ... materials. The equation is named after Edward Wight Washburn; also known as Lucas–Washburn equation, considering that Richard Lucas wrote a similar paper three years earlier, or the Bell-Cameron-Lucas-Washburn equation, considering J.M. Bell and F.K. Cameron's discovery of the form of the equation in 1906. Derivation In its most general form the Lucas Washburn equation describes the penetration length (L) of a liquid into a capillary pore or tube with time t as L=(Dt)^, where D is a simplified diffusion coefficient. This relationship, which holds true for a variety of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contact Angle
The contact angle (symbol ) is the angle between a liquid surface and a solid surface where they meet. More specifically, it is the angle between the surface tangent on the liquid–vapor interface and the tangent on the solid–liquid interface at their intersection. It quantifies the '' wettability'' of a solid surface by a liquid via the Young equation. A given system of solid, liquid, and vapor at a given temperature and pressure has a unique equilibrium contact angle. However, in practice a dynamic phenomenon of contact angle hysteresis is often observed, ranging from the advancing (maximal) contact angle to the receding (minimal) contact angle. The equilibrium contact is within those values, and can be calculated from them. The equilibrium contact angle reflects the relative strength of the liquid, solid, and vapour molecular interaction. The contact angle depends upon the medium above the free surface of the liquid, and the nature of the liquid and solid in contact. It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sessile Drop Technique
image:Contact angle.svg, 400px, An illustration of the sessile drop technique with a liquid droplet partially wetting a solid substrate. is the contact angle, and represent the solid–gas, gas–liquid, and liquid–solid interfaces, respectively. In materials science, the sessile drop technique is a method used for the characterization of solid surface energy, surface energies, and in some cases, aspects of liquid surface energies. The main premise of the method is that by placing a droplet of liquid with a known surface energy and contact angle, the surface energy of the solid substrate can be calculated. The liquid used for such experiments is referred to as the probe liquid, and the use of several different probe liquids is required. Probe liquid The surface energy is measured in units of joules per square meter, which is equivalent in the case of liquids to surface tension, measured in newtons per meter. The overall surface tension/energy of a liquid can be acquired throu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball (mathematics), ball cut off by a plane (mathematics), plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center (geometry), center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a ''Sphere#Hemisphere, hemisphere''. Volume and surface area The volume of the spherical cap and the area of the curved surface may be calculated using combinations of * The radius r of the sphere * The radius a of the base of the cap * The height h of the cap * The Spherical coordinate system, polar angle \theta between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk (mathematics), disk forming the base of the cap. These variables are inter-related through the formulas a = r \sin \theta, h = r ( 1 - \cos \theta ), 2hr = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraboloid Of Revolution
In geometry, a paraboloid is a quadric surface that has exactly one axial symmetry, axis of symmetry and no central symmetry, center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid made by a plane Parallel (geometry)#A line and a plane, parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit surface, implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Non-Newtonian Fluid Mechanics
A journal, from the Old French ''journal'' (meaning "daily"), may refer to: *Bullet journal, a method of personal organization *Diary, a record of personal secretive thoughts and as open book to personal therapy or used to feel connected to oneself. A record of what happened over the course of a day or other period *Daybook, also known as a general journal, a daily record of financial transactions *Logbook, a record of events important to the operation of a vehicle, facility, or otherwise *Transaction log, a chronological record of data processing *Travel journal, a record of the traveller's experience during the course of their journey In publishing, ''journal'' can refer to various periodicals or serials: *Academic journal, an academic or scholarly periodical **Scientific journal, an academic journal focusing on science **Medical journal, an academic journal focusing on medicine **Law review, a professional journal focusing on legal interpretation *Magazine, non-academic or scho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bingham Plastic
In materials science, a Bingham plastic is a viscoplastic material that behaves as a rigid body at low stresses but flows as a viscous fluid at high stress. It is named after Eugene C. Bingham who proposed its mathematical form in 1916. It is used as a common mathematical model of mud flow in drilling engineering, and in the handling of slurries. A common example is toothpaste, which will not be extruded until a certain pressure is applied to the tube. It is then pushed out as a relatively coherent plug. Explanation Figure 1 shows a graph of the behaviour of an ordinary viscous (or Newtonian) fluid in red, for example in a pipe. If the pressure at one end of a pipe is increased this produces a stress on the fluid tending to make it move (called the shear stress) and the volumetric flow rate increases proportionally. However, for a Bingham Plastic fluid (in blue), stress can be applied but it will not flow until a certain value, the yield stress, is reached. Beyond this poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics Of Fluids
''Physics of Fluids'' is a monthly peer-reviewed scientific journal covering fluid dynamics, established by the American Institute of Physics in 1958, and is published by AIP Publishing. The journal focus is the dynamics (physics), dynamics of gases, liquids, and complex or multiphase flow, multiphase fluids—and the journal contains original research resulting from theoretical physics, theoretical, computational fluid dynamics, computational, and experimental physics, experimental studies. History From 1958 through 1988, the journal included plasma (physics), plasma physics. From 1989 until 1993, the journal split into ''Physics of Fluids A'' covering fluid dynamics, and ''Physics of Fluids B,'' on plasma physics. In 1994, the latter was renamed ''Physics of Plasmas'', and the former continued under its original name, ''Physics of Fluids''. The journal was originally published by the American Institute of Physics in cooperation with the American Physical Society's Division of Fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |