|
Table Of Thermodynamic Equations
Common thermodynamic equations and quantities in thermodynamics, using mathematical notation, are as follows: Definitions Many of the definitions below are also used in the thermodynamics of chemical reactions. General basic quantities General derived quantities Thermal properties of matter Thermal transfer Equations The equations in this article are classified by subject. Thermodynamic processes Kinetic theory Ideal gas Entropy * S = k_\mathrm \ln \Omega , where ''k''B is the Boltzmann constant, and Ω denotes the volume of macrostate in the phase space or otherwise called thermodynamic probability. * dS = \frac , for reversible processes only Statistical physics Below are useful results from the Maxwell–Boltzmann distribution for an ideal gas, and the implications of the Entropy quantity. The distribution is valid for atoms or molecules constituting ideal gases. Corollaries of the non-relativistic Maxwell–Boltzmann dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Equations
Thermodynamics is expressed by a mathematical framework of ''thermodynamic equations'' which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics. Introduction One of the fundamental thermodynamic equations is the description of thermodynamic work in analogy to mechanical work, or weight lifted through an elevation against gravity, as defined in 1824 by French physicist Sadi Carnot. Carnot used the phrase motive power for work. In the footnotes to his famous ''On the Motive Power of Fire'', he states: “We use here the expression ''motive power'' to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.” With the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of Thermodynamic free energy, free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial Molar concentration, molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
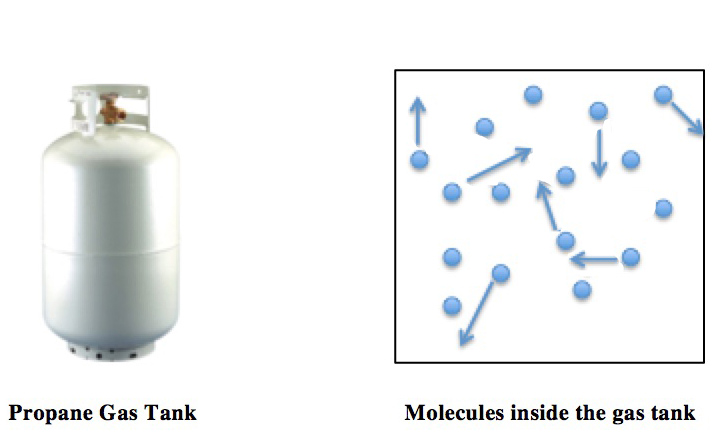
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
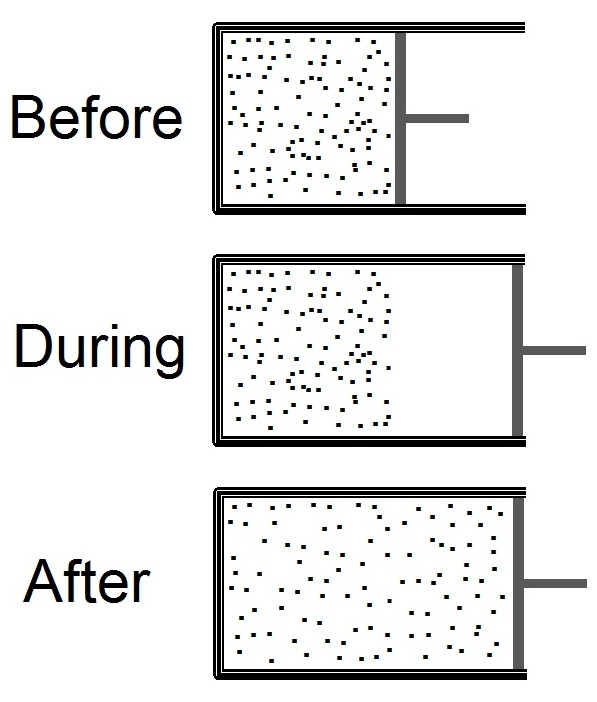
Joule Expansion
The Joule expansion (a subset of free expansion) is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container (via a small partition), with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container. The Joule expansion, treated as a thought experiment involving ideal gases, is a useful exercise in classical thermodynamics. It provides a convenient example for calculating changes in thermodynamic quantities, including the resulting increase in entropy of the universe (entropy production) that results from this inherently irreversible process. An actual Joule expansion experiment necessarily involves real gases; the temperature change in such a process provides a measure of intermolecular forces. This type of expansion is named after James Prescott Joule who used this expansion, in 1845, in his study for the mechanical e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isochoric Process
In thermodynamics, an isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant. An isochoric process is exemplified by the heating or the cooling of the contents of a sealed, inelastic container: The thermodynamic process is the addition or removal of heat; the isolation of the contents of the container establishes the closed system; and the inability of the container to deform imposes the constant-volume condition. Formalism An isochoric thermodynamic quasi-static process is characterized by constant volume, i.e., .Ansermet, J.-P., Brechet, S.D. (2019). ''Principles of Thermodynamics'', Cambridge University Press, Cambridge UK, p. 113. The process does no pressure-volume work, since such work is defined by W = P \Delta V , where is pressure. The sign convention is such that positive work is performed by the sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isobaric Process
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the Thermodynamic system, system stays constant: Δ''P'' = 0. The heat transferred to the system does work (thermodynamics), work, but also changes the internal energy (''U'') of the system. This article uses the physics sign convention for work, where positive work is work (thermodynamics)#Sign convention, work done by the system. Using this convention, by the first law of thermodynamics, : Q = \Delta U + W\, where ''W'' is work, ''U'' is internal energy, and ''Q'' is heat. Pressure-volume work by the closed system is defined as: :W = \int \! p \,dV \, where Δ means change over the whole process, whereas ''d'' denotes a differential. Since pressure is constant, this means that : W = p \Delta V\, . Applying the ideal gas law, this becomes : W = n\,R\,\Delta T with ''R'' representing the gas constant, and ''n'' representing the amount of substance, which is ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Process
An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an '' adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The noun '' isotherm'' is derived from the Ancient Greek words (), meaning "equal", and (), meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic Process
An isentropic process is an idealized thermodynamic process that is both Adiabatic process, adiabatic and Reversible process (thermodynamics), reversible. The work (physics), work transfers of the system are friction, frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamics, Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" derives from the proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
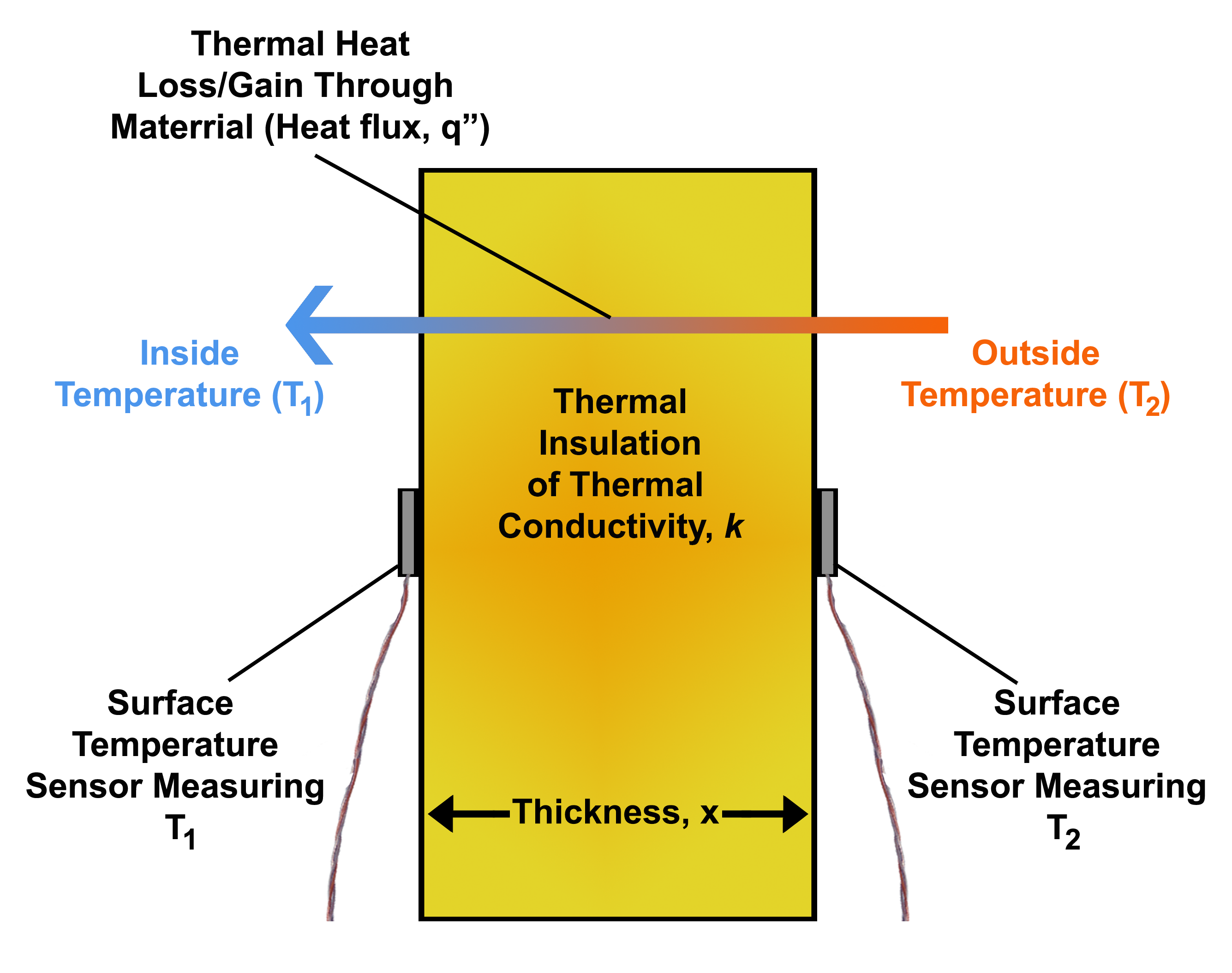
Heat Flux
In physics and engineering, heat flux or thermal flux, sometimes also referred to as heat flux density, heat-flow density or heat-flow rate intensity, is a flow of energy per unit area per unit time (physics), time. Its SI units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a Vector (geometric), vector quantity. To define the heat flux at a certain point in space, one takes the Limiting case (mathematics), limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''Mass flux, mass'' or Transport phenomena, ''momentum'' flux. Heat conduction#Fourier's law, Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by thermal conduction, conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature Gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature spatial gradient is a vector quantity with Dimensional analysis, dimension of temperature difference per unit length. The International System of Units, SI Units of measurement, unit is kelvin per meter (K/m). Temperature gradients in the Earth's atmosphere, atmosphere are important in the atmospheric sciences (meteorology, climatology and related fields). Mathematical description Assuming that the temperature ''T'' is an intensive quantity, i.e., a single-valued, Continuous function, continuous and Derivative, differentiable Function (mathematics), function of three-dimensional space (often called a scalar field), i.e., that :T=T(x,y,z) where ''x'', ''y'' and ''z'' are the Cartesian coordinate system, coordinates of the location of interest, then the temperature gradient is the vector (geometric) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summarized and extended the work of his predecessors in his five-volume Traité de mécanique céleste, ''Mécanique céleste'' (''Celestial Mechanics'') (1799–1825). This work translated the geometric study of classical mechanics to one based on calculus, opening up a broader range of problems. Laplace also popularized and further confirmed Isaac Newton, Sir Isaac Newton's work. In statistics, the Bayesian probability, Bayesian interpretation of probability was developed mainly by Laplace. Laplace formulated Laplace's equation, and pioneered the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplace operator, Laplacian differential operator, widely used in mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the '' isentropic expansion factor'' and is denoted by (gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |