|
Tuple
In mathematics, a tuple is a finite ordered list (sequence) of elements. An -tuple is a sequence (or ordered list) of elements, where is a non-negative integer. There is only one 0-tuple, referred to as ''the empty tuple''. An -tuple is defined inductively using the construction of an ordered pair. Mathematicians usually write tuples by listing the elements within parentheses "" and separated by a comma and a space; for example, denotes a 5-tuple. Sometimes other symbols are used to surround the elements, such as square brackets " nbsp; or angle brackets "⟨ ⟩". Braces "" are used to specify arrays in some programming languages but not in mathematical expressions, as they are the standard notation for sets. The term ''tuple'' can often occur when discussing other mathematical objects, such as vectors. In computer science, tuples come in many forms. Most typed functional programming languages implement tuples directly as product types, tightly associated with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relational Algebra
In database theory, relational algebra is a theory that uses algebraic structures with a well-founded semantics for modeling data, and defining queries on it. The theory was introduced by Edgar F. Codd. The main application of relational algebra is to provide a theoretical foundation for relational databases, particularly query languages for such databases, chief among which is SQL. Relational databases store tabular data represented as relations. Queries over relational databases often likewise return tabular data represented as relations. The main purpose of the relational algebra is to define operators that transform one or more input relations to an output relation. Given that these operators accept relations as input and produce relations as output, they can be combined and used to express potentially complex queries that transform potentially many input relations (whose data are stored in the database) into a single output relation (the query results). Unary operators a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
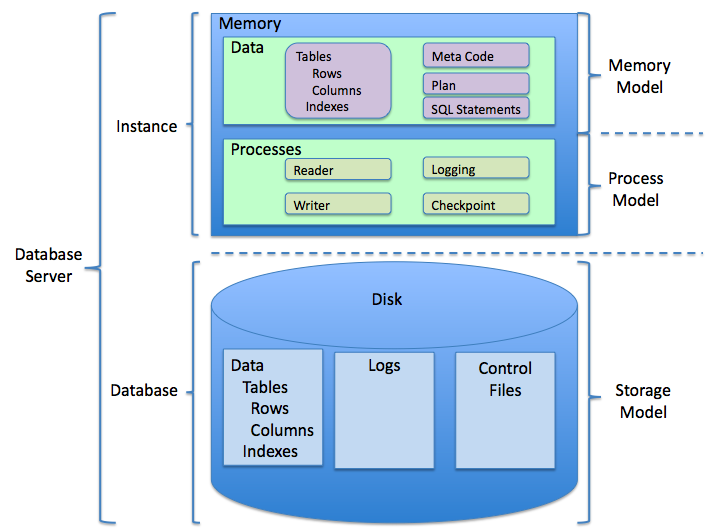
Relational Database
A relational database is a (most commonly digital) database based on the relational model of data, as proposed by E. F. Codd in 1970. A system used to maintain relational databases is a relational database management system (RDBMS). Many relational database systems are equipped with the option of using the SQL (Structured Query Language) for querying and maintaining the database. History The term "relational database" was first defined by E. F. Codd at IBM in 1970. Codd introduced the term in his research paper "A Relational Model of Data for Large Shared Data Banks". In this paper and later papers, he defined what he meant by "relational". One well-known definition of what constitutes a relational database system is composed of Codd's 12 rules. However, no commercial implementations of the relational model conform to all of Codd's rules, so the term has gradually come to describe a broader class of database systems, which at a minimum: # Present the data to the user as rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordered Pair
In mathematics, an ordered pair (''a'', ''b'') is a pair of objects. The order in which the objects appear in the pair is significant: the ordered pair (''a'', ''b'') is different from the ordered pair (''b'', ''a'') unless ''a'' = ''b''. (In contrast, the unordered pair equals the unordered pair .) Ordered pairs are also called 2-tuples, or sequences (sometimes, lists in a computer science context) of length 2. Ordered pairs of scalars are sometimes called 2-dimensional vectors. (Technically, this is an abuse of terminology since an ordered pair need not be an element of a vector space.) The entries of an ordered pair can be other ordered pairs, enabling the recursive definition of ordered ''n''-tuples (ordered lists of ''n'' objects). For example, the ordered triple (''a'',''b'',''c'') can be defined as (''a'', (''b'',''c'')), i.e., as one pair nested in another. In the ordered pair (''a'', ''b''), the object ''a'' is called the ''first entry'', and the object ''b'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Type
In programming languages and type theory, a product of ''types'' is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed order, but otherwise may contain all possible instances of its primitive data types. The expression of an instance of a product type will be a tuple, and is called a "tuple type" of expression. A product of types is a direct product of two or more types. If there are only two component types, it can be called a "pair type". For example, if two component types A and B are the set of all possible values of that type, the product type written A × B contains elements that are pairs (a,b), where "a" and "b" are instances of A and B respectively. The pair type is a special case of the dependent pair type, where the type B may depend on the instance picked from A. In many languages, product t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (mathematics And Physics)
In mathematics and physics, vector is a term that refers colloquially to some quantities that cannot be expressed by a single number (a scalar), or to elements of some vector spaces. Historically, vectors were introduced in geometry and physics (typically in mechanics) for quantities that have both a magnitude and a direction, such as displacements, forces and velocity. Such quantities are represented by geometric vectors in the same way as distances, masses and time are represented by real numbers. The term ''vector'' is also used, in some contexts, for tuples, which are finite sequences of numbers of a fixed length. Both geometric vectors and tuples can be added and scaled, and these vector operations led to the concept of a vector space, which is a set equipped with a vector addition and a scalar multiplication that satisfy some axioms generalizing the main properties of operations on the above sorts of vectors. A vector space formed by geometric vectors is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Assignment (computer Science)
In computer programming, an assignment statement sets and/or re-sets the value stored in the storage location(s) denoted by a variable name; in other words, it copies a value into the variable. In most imperative programming languages, the assignment statement (or expression) is a fundamental construct. Today, the most commonly used notation for this operation is ''x'' = ''expr'' (originally Superplan 1949–51, popularized by Fortran 1957 and C). The second most commonly used notation is ''x'' := ''expr'' (originally ALGOL 1958, popularised by Pascal). Many other notations are also in use. In some languages, the symbol used is regarded as an operator (meaning that the assignment statement as a whole returns a value). Other languages define assignment as a statement (meaning that it cannot be used in an expression). Assignments typically allow a variable to hold different values at different times during its life-span and scope. However, some languages (primarily strictl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Row (database)
In the context of a relational database, a row—also called a tuple—represents a single, implicitly structured data item in a table. In simple terms, a database table can be thought of as consisting of ''rows'' and columns. Cory Janssen, Techopedia, retrieved 27 June 2014 Each row in a table represents a set of related data, and every row in the table has the same structure. For example, in a table that represents companies, each row would represent a single company. Columns might represent things like company name, company street address, whether the company is publicly held, its , etc. In a table that represents ''the as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Array Data Type
In computer science, array is a data type that represents a collection of ''elements'' ( values or variables), each selected by one or more indices (identifying keys) that can be computed at run time during program execution. Such a collection is usually called an array variable or array value.Robert W. Sebesta (2001) ''Concepts of Programming Languages''. Addison-Wesley. 4th edition (1998), 5th edition (2001), By analogy with the mathematical concepts vector and matrix, array types with one and two indices are often called vector type and matrix type, respectively. More generally, a multidimensional array type can be called a tensor type, by anology with the physical concept, tensor. Language support for array types may include certain built-in array data types, some syntactic constructions (''array type constructors'') that the programmer may use to define such types and declare array variables, and special notation for indexing array elements. For example, in the Pasc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Record (computer Science)
In computer science, a record (also called a structure, struct, or compound data) is a basic data structure. Records in a database or spreadsheet are usually called "rows". A record is a collection of '' fields'', possibly of different data types, typically in a fixed number and sequence. The fields of a record may also be called ''members'', particularly in object-oriented programming; fields may also be called ''elements'', though this risks confusion with the elements of a collection. For example, a date could be stored as a record containing a numeric year field, a month field represented as a string, and a numeric day-of-month field. A personnel record might contain a name, a salary, and a rank. A Circle record might contain a center and a radius—in this instance, the center itself might be represented as a point record containing x and y coordinates. Records are distinguished from arrays by the fact that their number of fields is determined in the definition of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Data Type
In computer programming, especially functional programming and type theory, an algebraic data type (ADT) is a kind of composite type, i.e., a type formed by combining other types. Two common classes of algebraic types are product types (i.e., tuples and records) and sum types (i.e., tagged or disjoint unions, coproduct types or ''variant types''). The values of a product type typically contain several values, called ''fields''. All values of that type have the same combination of field types. The set of all possible values of a product type is the set-theoretic product, i.e., the Cartesian product, of the sets of all possible values of its field types. The values of a sum type are typically grouped into several classes, called ''variants''. A value of a variant type is usually created with a quasi-functional entity called a ''constructor''. Each variant has its own constructor, which takes a specified number of arguments with specified types. The set of all possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ploidy
Ploidy () is the number of complete sets of chromosomes in a cell, and hence the number of possible alleles for autosomal and pseudoautosomal genes. Sets of chromosomes refer to the number of maternal and paternal chromosome copies, respectively, in each homologous chromosome pair, which chromosomes naturally exist as. Somatic cells, tissues, and individual organisms can be described according to the number of sets of chromosomes present (the "ploidy level"): monoploid (1 set), diploid (2 sets), triploid (3 sets), tetraploid (4 sets), pentaploid (5 sets), hexaploid (6 sets), heptaploid or septaploid (7 sets), etc. The generic term polyploid is often used to describe cells with three or more chromosome sets. Virtually all sexually reproducing organisms are made up of somatic cells that are diploid or greater, but ploidy level may vary widely between different organisms, between different tissues within the same organism, and at different stages in an organism's life cycle. Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
