|
Total Correlation
In probability theory and in particular in information theory, total correlation (Watanabe 1960) is one of several generalizations of the mutual information. It is also known as the ''multivariate constraint'' (Garner 1962) or ''multiinformation'' (Studený & Vejnarová 1999). It quantifies the redundancy or dependency among a set of ''n'' random variables. Definition For a given set of ''n'' random variables \, the total correlation C(X_1,X_2,\ldots,X_n) is defined as the Kullback–Leibler divergence from the joint distribution p(X_1, \ldots, X_n) to the independent distribution of p(X_1)p(X_2)\cdots p(X_n), :C(X_1, X_2, \ldots, X_n) \equiv \operatorname\left p(X_1)p(X_2)\cdots p(X_n)\right\; . This divergence reduces to the simpler difference of entropies, :C(X_1,X_2,\ldots,X_n) = \left sum_^n H(X_i)\right- H(X_1, X_2, \ldots, X_n) where H(X_) is the information entropy of variable X_i \,, and H(X_1,X_2,\ldots,X_n) is the joint entropy of the variable set \. In terms of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
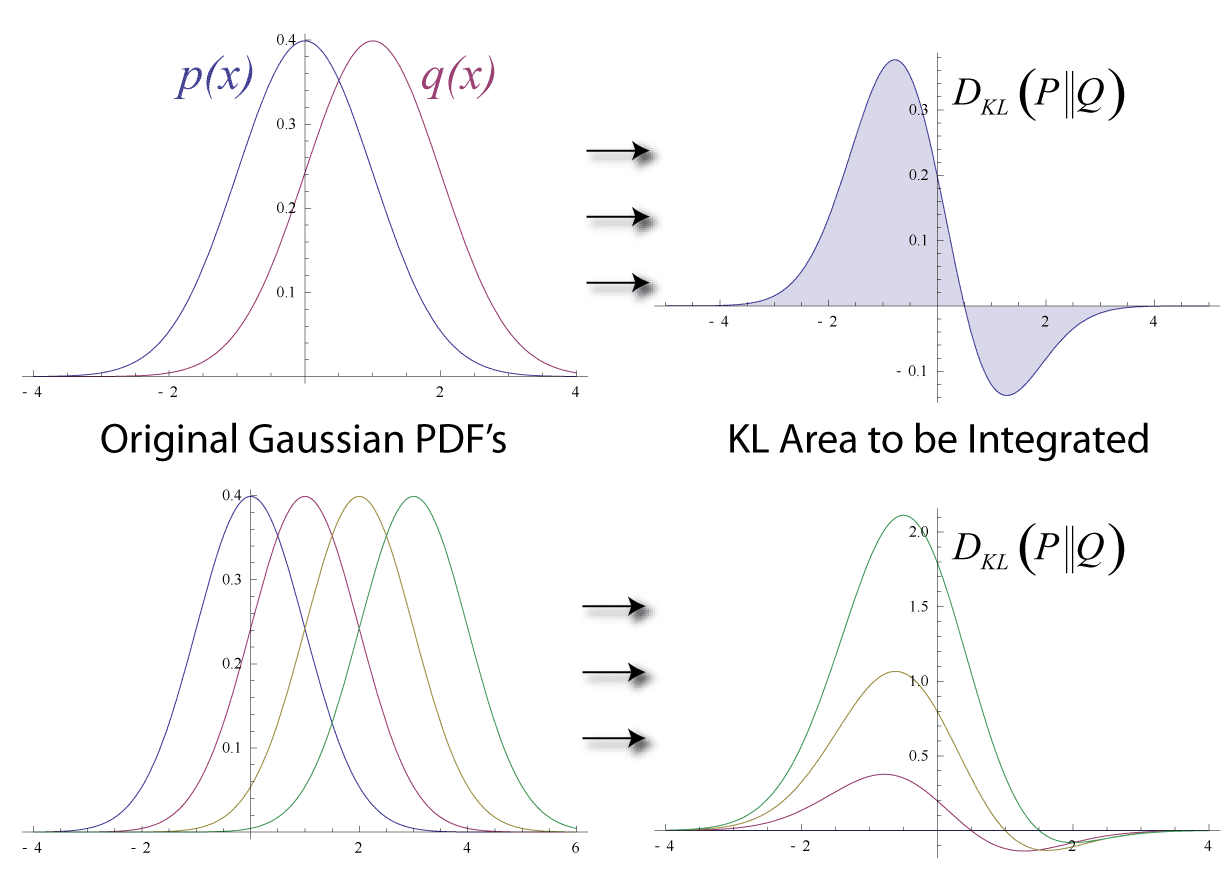 |
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Information Entropy
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to , 1/math>, the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Joint Entropy
In information theory, joint entropy is a measure of the uncertainty associated with a set of variables. Definition The joint Shannon entropy (in bits) of two discrete random variables X and Y with images \mathcal X and \mathcal Y is defined as :\Eta(X,Y) = -\sum_ \sum_ P(x,y) \log_2 (x,y)/math> where x and y are particular values of X and Y, respectively, P(x,y) is the joint probability of these values occurring together, and P(x,y) \log_2 (x,y)/math> is defined to be 0 if P(x,y)=0. For more than two random variables X_1, ..., X_n this expands to :\Eta(X_1, ..., X_n) = -\sum_ ... \sum_ P(x_1, ..., x_n) \log_2 (x_1, ..., x_n)/math> where x_1,...,x_n are particular values of X_1,...,X_n, respectively, P(x_1, ..., x_n) is the probability of these values occurring together, and P(x_1, ..., x_n) \log_2 (x_1, ..., x_n)/math> is defined to be 0 if P(x_1, ..., x_n)=0. Properties Nonnegativity The joint entropy of a set of random variables is a nonnegative number. :\Eta(X,Y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprisal from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Cluster Analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the analyst) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistics, statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis refers to a family of algorithms and tasks rather than one specific algorithm. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small Distance function, distances between cluster members, dense areas of the data space, intervals or pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Feature Selection
In machine learning, feature selection is the process of selecting a subset of relevant Feature (machine learning), features (variables, predictors) for use in model construction. Feature selection techniques are used for several reasons: * simplification of models to make them easier to interpret, * shorter training times, * to avoid the curse of dimensionality, * improve the compatibility of the data with a certain learning model class, * to encode inherent Symmetric space, symmetries present in the input space. The central premise when using feature selection is that data sometimes contains features that are ''redundant'' or ''irrelevant'', and can thus be removed without incurring much loss of information. Redundancy and irrelevance are two distinct notions, since one relevant feature may be redundant in the presence of another relevant feature with which it is strongly correlated. Feature extraction creates new features from functions of the original features, whereas feat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Dual Total Correlation
In information theory, dual total correlation, information rate, excess entropy,Nihat Ay, E. Olbrich, N. Bertschinger (2001). A unifying framework for complexity measures of finite systems. European Conference on Complex Systemspdf or binding information is one of several known non-negative generalizations of mutual information. While total correlation is bounded by the sum entropies of the ''n'' elements, the dual total correlation is bounded by the joint-entropy of the ''n'' elements. Although well behaved, dual total correlation has received much less attention than the total correlation. A measure known as "TSE-complexity" defines a continuum between the total correlation and dual total correlation. Definition For a set of ''n'' random variables \, the dual total correlation D(X_1,\ldots, X_n) is given by : D(X_1,\ldots, X_n) = H\left( X_1, \ldots, X_n \right) - \sum_^n H\left( X_i \mid X_1, \ldots, X_, X_, \ldots, X_n \right) , where H(X_,\ldots, X_) is the joint entr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |