|
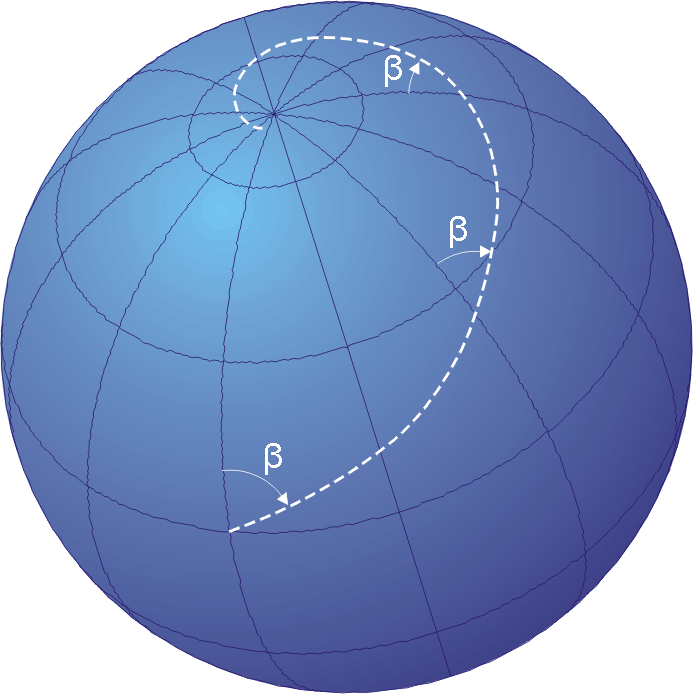
Seiffert's Spiral
Seiffert's spherical spiral is a curve on a sphere made by moving on the sphere with constant speed and angular velocity with respect to a fixed diameter. If the selected diameter is the line from the north pole to the south pole, then the requirement of constant angular velocity means that the longitude of the moving point changes at a constant rate. The cylindrical coordinates of the varying point on this curve are given by the Jacobian elliptic functions. Formulation Symbols Representation via equations The Seiffert's spherical spiral can be expressed as r = \operatorname(s, k),\, \theta = k \cdot s \text z = \operatorname(s, k) or expressed as Jacobi theta functions In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field ... r = \frac,\, \theta = \frac \cdot s \text z = \fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve On A Sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so most balls used in sports and toys are spherical, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Elliptic Function
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacobi ellipti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobi Elliptic Functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacobi ellipti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobi Theta Functions
In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory. The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables (conventionally called ), a theta function has a property expressing its behavior with respect to the addition of a period of the associated elliptic functions, making it a quasiperiodic function. In the abstract theory this quasiperiodicity comes from the cohomology class of a line bundle on a complex torus, a condition of descent. One interpretation of theta functions when dealing with the heat equation is that "a theta function is a special function that describes the evolution of temperature on a segment domain subject to certain boundary conditions". Throughout this article, (e^)^ sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Modulus
In mathematics, the modular lambda function λ(τ)\lambda(\tau) is not a modular function (per the Wikipedia definition), but every modular function is a rational function in \lambda(\tau). Some authors use a non-equivalent definition of "modular functions". is a highly symmetric holomorphic function on the complex upper half-plane. It is invariant under the fractional linear action of the congruence group Γ(2), and generates the function field of the corresponding quotient, i.e., it is a Hauptmodul for the modular curve ''X''(2). Over any point τ, its value can be described as a cross ratio of the branch points of a ramified double cover of the projective line by the elliptic curve \mathbb/\langle 1, \tau \rangle, where the map is defined as the quotient by the minus;1involution. The q-expansion, where q = e^ is the nome, is given by: : \lambda(\tau) = 16q - 128q^2 + 704 q^3 - 3072q^4 + 11488q^5 - 38400q^6 + \dots. By symmetrizing the lambda function under the canon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhumb Line
In navigation, a rhumb line, rhumb (), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature, whereas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spirals
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:Spiral ''American Heritage Dictionary of the English Language'', Houghton Mifflin Company, Fourth Edition, 2009. # a curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point. # a three-dimensional curve that turns around an axis at a constant or continuously varying distance while moving parallel to the axis; a . The first definition describes a |