|
Supermodular Function
In mathematics, a supermodular function is a function on a lattice that, informally, has the property of being characterized by "increasing differences." Seen from the point of set functions, this can also be viewed as a relationship of "increasing returns", where adding more elements to a subset increases its valuation. In economics, supermodular functions are often used as a formal expression of complementarity in preferences among goods. Supermodular functions are studied and have applications in game theory, economics, lattice theory, combinatorial optimization, and machine learning. Definition Let (X, \preceq) be a lattice. A real-valued function f: X \rightarrow \mathbb is called supermodular if f(x \vee y) + f(x \wedge y) \geq f(x) + f(y) for all x, y \in X. If the inequality is strict, then f is strictly supermodular on X. If -f is (strictly) supermodular then ''f'' is called (strictly) submodular. A function that is both submodular and supermodular is called modula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (order)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join (mathematics), join) and a unique infimum (also called a greatest lower bound or meet (mathematics), meet). An example is given by the power set of a set, partially ordered by Subset, inclusion, for which the supremum is the Union (set theory), union and the infimum is the Intersection (set theory), intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic Identity (mathematics), identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilatti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
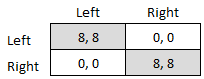
Coordination Game
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibrium, Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization Of Ordered Sets
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Optimization problems can be divided into two categories, depending on whether the variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems in general (although one usually is also interested in the actual difference of two numbers, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility Functions On Indivisible Goods
Some branches of economics and game theory deal with indivisible goods, discrete items that can be traded only as a whole. For example, in combinatorial auctions there is a finite set of items, and every agent can buy a subset of the items, but an item cannot be divided among two or more agents. It is usually assumed that every agent assigns subjective utility to every subset of the items. This can be represented in one of two ways: * An ordinal utility preference relation, usually marked by \succ. The fact that an agent prefers a set A to a set B is written A \succ B. If the agent only weakly prefers A (i.e. either prefers A or is indifferent between A and B) then this is written A \succeq B. * A cardinal utility function, usually denoted by u. The utility an agent gets from a set A is written u(A). Cardinal utility functions are often normalized such that u(\emptyset)=0, where \emptyset is the empty set. A cardinal utility function implies a preference relation: u(A)>u(B) implies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superadditive
In mathematics, a function f is superadditive if f(x+y) \geq f(x) + f(y) for all x and y in the domain of f. Similarly, a sequence a_1, a_2, \ldots is called superadditive if it satisfies the inequality a_ \geq a_n + a_m for all m and n. The term "superadditive" is also applied to functions from a boolean algebra to the real numbers where P(X \lor Y) \geq P(X) + P(Y), such as lower probabilities. Examples of superadditive functions * The map f(x) = x^2 is a superadditive function for nonnegative real numbers because f(x + y) = (x + y)^2 = x^2 + y^2 + 2 x y = f(x) + f(y) + 2 x y \ge f(x) + f(y). * The determinant is superadditive for nonnegative Hermitian matrix, that is, if A, B \in \text_n(\Complex) are nonnegative Hermitian then \det(A + B) \geq \det(A) + \det(B). This follows from the Minkowski determinant theorem, which more generally states that \det(\cdot)^ is superadditive (equivalently, concave) for nonnegative Hermitian matrices of size n: If A, B \in \text_n(\Com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-Boolean Function
In mathematics and optimization, a pseudo-Boolean function is a function of the form :f: \mathbf^n \to \R, where is a ''Boolean domain'' and is a nonnegative integer called the arity of the function. A Boolean function is then a special case, where the values are also restricted to 0 or 1. Representations Any pseudo-Boolean function can be written uniquely as a multi-linear polynomial: :f(\boldsymbol) = a + \sum_i a_ix_i + \sum_a_x_ix_j + \sum_a_x_ix_jx_k + \ldots The degree of the pseudo-Boolean function is simply the degree of the polynomial in this representation. In many settings (e.g., in Fourier analysis of pseudo-Boolean functions), a pseudo-Boolean function is viewed as a function f that maps \^n to \mathbb. Again in this case we can uniquely write f as a multi-linear polynomial: f(x)= \sum_\hat(I)\prod_x_i, where \hat(I) are Fourier coefficients of f and \. Optimization Minimizing (or, equivalently, maximizing) a pseudo-Boolean function is NP-hard. This can easil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Submodular Set Function
In mathematics, a submodular set function (also known as a submodular function) is a set function that, informally, describes the relationship between a set of inputs and an output, where adding more of one input has a decreasing additional benefit ( diminishing returns). The natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory (as functions modeling user preferences) and electrical networks. Recently, submodular functions have also found utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains. Definition If \Omega is a finite set, a submodular function is a set function f:2^\rightarrow \mathbb, where 2^\Omega denotes the power set of \Omega, which satisfies one of the following equivalent condit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Economic Theory
The ''Journal of Economic Theory'' is a bimonthly peer-reviewed academic journal covering the field of economic theory. Karl Shell has served as editor-in-chief of the journal since it was established in 1968. Since 2000, he has shared the editorship with Jess Benhabib, Alessandro Lizzeri, Christian Hellwig, and more recently with Alessandro Pavan, Ricardo Lagos (economist), Ricardo Lagos, Marciano Siniscalchi, and Xavier Vives. The journal is published by Elsevier. In 2020, Tilman Börgers was chief editor of the journal. Abstracting and indexing According to the ''Journal Citation Reports'', the journal has a 2020 impact factor of 1.458. See also *List of economics journals References External links * Economics journals Elsevier academic journals Academic journals established in 1969 English-language journals Bimonthly journals {{econ-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complementary Goods
In economics, a complementary good is a good whose appeal increases with the popularity of its complement. Technically, it displays a negative cross elasticity of demand and that demand for it increases when the price of another good decreases. If A is a complement to B, an increase in the price of A will result in a negative movement along the demand curve of A and cause the demand curve for B to shift inward; less of each good will be demanded. Conversely, a decrease in the price of A will result in a positive movement along the demand curve of A and cause the demand curve of B to shift outward; more of each good will be demanded. This is in contrast to a substitute good, whose demand decreases when its substitute's price decreases. When two goods are complements, they experience ''joint demand'' - the demand of one good is linked to the demand for another good. Therefore, if a higher quantity is demanded of one good, a higher quantity will also be demanded of the other, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility Function
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a Normative economics, normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original Utilitarianism, utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill. * In a Positive economics, descriptive context, the term refers to an ''apparent'' objective function; such a function is Revealed preference, revealed by a person's behavior, and specifically by their preferences over Lottery (decision theory), lotteries, which can be any quantified choice. The relationship between these two kinds of utility functions has been a source of controversy among both Economics, economists and Ethics, ethicists, with most maintaining that the two are distinct but generally re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imperfect Competition
In economics, imperfect competition refers to a situation where the characteristics of an economic market do not fulfil all the necessary conditions of a perfectly competitive market. Imperfect competition causes market inefficiencies, resulting in market failure. Imperfect competition usually describes behaviour of suppliers in a market, such that the level of competition between sellers is below the level of competition in perfectly competitive market conditions. The competitive structure of a market can significantly impact the financial performance and conduct of the firms competing within it. There is a causal relationship between competitive structure, behaviour and performance paradigm. Market structure can be determined by measuring the degree of suppliers' market concentration, which in turn reveals the nature of market competition. The degree of market power refers to firms' ability to affect the price of a good and thus, raise the market price of the good or service abov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |