|
Sieve Of Eratosthenes
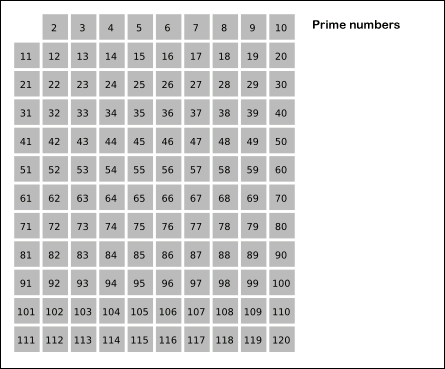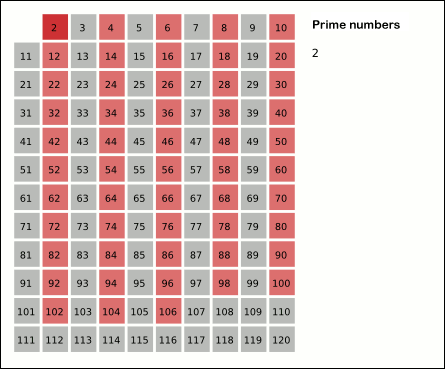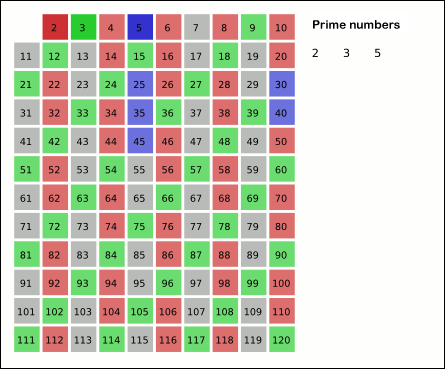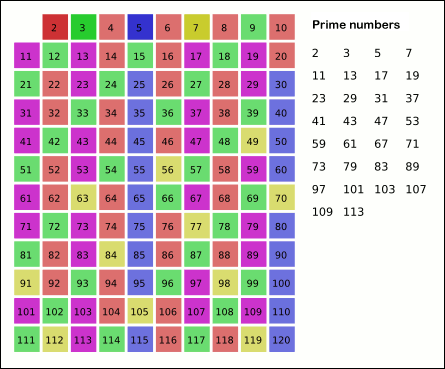
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Animation Sieve Of Eratosth
Animation is a filmmaking technique whereby image, still images are manipulated to create Motion picture, moving images. In traditional animation, images are drawn or painted by hand on cel, transparent celluloid sheets to be photographed and exhibited on film. Animation has been recognised as an artistic medium, specifically within the Entertainment#Industry, entertainment industry. Many animations are either traditional animations or computer animations made with computer-generated imagery (CGI). Stop motion animation, in particular claymation, has continued to exist alongside these other forms. Animation is contrasted with live action, although the two do not exist in isolation. Many moviemakers have produced Live-action animation, films that are a hybrid of the two. As CGI increasingly Photorealism, approximates photographic imagery, filmmakers can easily Compositing, composite 3D animations into their film rather than using practical effects for showy visual effects (VFX). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Data Type
In computer science, the Boolean (sometimes shortened to Bool) is a data type that has one of two possible values (usually denoted ''true'' and ''false'') which is intended to represent the two truth values of logic and Boolean algebra. It is named after George Boole, who first defined an algebraic system of logic in the mid 19th century. The Boolean data type is primarily associated with conditional statements, which allow different actions by changing control flow depending on whether a programmer-specified Boolean ''condition'' evaluates to true or false. It is a special case of a more general ''logical data type—''logic does not always need to be Boolean (see probabilistic logic). Generalities In programming languages with a built-in Boolean data type, such as Pascal, C, Python or Java, the comparison operators such as > and ≠ are usually defined to return a Boolean value. Conditional and iterative commands may be defined to test Boolean-valued expressions. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Communications Of The ACM
''Communications of the ACM'' (''CACM'') is the monthly journal of the Association for Computing Machinery (ACM). History It was established in 1958, with Saul Rosen as its first managing editor. It is sent to all ACM members. Articles are intended for readers with backgrounds in all areas of computer science and information systems. The focus is on the practical implications of advances in information technology and associated management issues; ACM also publishes a variety of more theoretical journals. The magazine straddles the boundary of a science magazine, trade magazine, and a scientific journal. While the content is subject to peer review, the articles published are often summaries of research that may also be published elsewhere. Material published must be accessible and relevant to a broad readership. From 1960 onward, ''CACM'' also published algorithms, expressed in ALGOL. The collection of algorithms later became known as the Collected Algorithms of the ACM. CA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Of The Euler Product Formula For The Riemann Zeta Function
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis ''Variae observationes circa series infinitas'' (''Various Observations about Infinite Series''), published by St Petersburg Academy in 1737. John Derbyshire (2003), chapter 7, "The Golden Key, and an Improved Prime Number Theorem" The Euler product formula The Euler product formula for the Riemann zeta function reads :\zeta(s) = \sum_^\infty\frac = \prod_ \frac where the left hand side equals the Riemann zeta function: :\zeta(s) = \sum_^\infty\frac = 1+\frac+\frac+\frac+\frac+ \ldots and the product on the right hand side extends over all prime numbers ''p'': :\prod_ \frac = \frac\cdot\frac\cdot\frac\cdot\frac \cdots \frac \cdots Proof of the Euler product formula This sketch of a proof makes use of simple algebra only. This was the method by which Euler originally discovered the formula. There is a certain sieving property that we can use to our advantage: :\zeta(s) = 1+\frac+\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Complexity
The bit is the most basic unit of information in computing and digital communication. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented as either , but other representations such as ''true''/''false'', ''yes''/''no'', ''on''/''off'', or ''+''/''−'' are also widely used. The relation between these values and the physical states of the underlying storage or device is a matter of convention, and different assignments may be used even within the same device or program. It may be physically implemented with a two-state device. A contiguous group of binary digits is commonly called a '' bit string'', a bit vector, or a single-dimensional (or multi-dimensional) ''bit array''. A group of eight bits is called one ''byte'', but historically the size of the byte is not strictly defined. Frequently, half, full, double and quadruple words consist of a number of bytes which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-polynomial Time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is a polynomial in the ''numeric value'' of the input (the largest integer present in the input)—but not necessarily in the ''length'' of the input (the number of bits required to represent it), which is the case for polynomial time algorithms.Michael R. Garey and David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, 1979. In general, the numeric value of the input is exponential in the input length, which is why a pseudo-polynomial time algorithm does not necessarily run in polynomial time with respect to the input length. An NP-complete problem with known pseudo-polynomial time algorithms is called weakly NP-complete. An NP-complete problem is called strongly NP-complete if it is proven that it cannot be solved by a pseudo-polynomial time algorithm unless . The strong/weak kinds of NP-hardness are defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Harmonic Series
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Access Machine
In computer science, random-access machine (RAM or RA-machine) is a model of computation that describes an abstract machine in the general class of register machines. The RA-machine is very similar to the counter machine but with the added capability of 'indirect addressing' of its registers. The 'registers' are intuitively equivalent to main memory of a common computer, except for the additional ability of registers to store natural numbers of any size. Like the counter machine, the RA-machine contains the execution instructions in the finite-state portion of the machine (the so-called Harvard architecture). The RA-machine's equivalent of the universal Turing machinewith its program in the registers as well as its datais called the random-access stored-program machine or RASP-machine. It is an example of the so-called von Neumann architecture and is closest to the common notion of a computer. Together with the Turing machine and counter-machine models, the RA-machine and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dataflow Programming
In computer programming, dataflow programming is a programming paradigm that models a program as a directed graph of the data flowing between operations, thus implementing dataflow principles and architecture. Dataflow programming languages share some features of functional languages, and were generally developed in order to bring some functional concepts to a language more suitable for numeric processing. Some authors use the term ''datastream'' instead of ''dataflow'' to avoid confusion with dataflow computing or dataflow architecture, based on an indeterministic machine paradigm. Dataflow programming was pioneered by Jack Dennis and his graduate students at MIT in the 1960s. Considerations Traditionally, a program is modelled as a series of operations happening in a specific order; this may be referred to as sequential, procedural, control flow (indicating that the program chooses a specific path), or imperative programming. The program focuses on commands, in line with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |