|
Schläfli Orthoscheme
In geometry, a Schläfli orthoscheme is a type of simplex. The orthoscheme is the generalization of the right triangle to simplex figures of any number of dimensions. Orthoschemes are defined by a sequence of Edge (geometry), edges (v_0v_1), (v_1v_2), \dots, (v_v_d) \, that are mutually orthogonal. They were introduced by Ludwig Schläfli, who called them ''orthoschemes'' and studied their volume in Euclidean space, Euclidean, Hyperbolic geometry, hyperbolic, and spherical geometry, spherical geometries. H. S. M. Coxeter later named them after Schläfli. As right triangles provide the basis for trigonometry, orthoschemes form the basis of a trigonometry of ''n'' dimensions, as developed by Pieter Hendrik Schoute, Schoute who called it polygonometry. Jean-Pierre Sydler, J.-P. Sydler and Børge Jessen studied orthoschemes extensively in connection with Hilbert's third problem. Orthoschemes, also called path-simplices in the applied mathematics literature, are a special case of a mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miroslav Fiedler
Miroslav Fiedler (7 April 1926 – 20 November 2015) was a Czech mathematician known for his contributions to linear algebra, graph theory and algebraic graph theory. His article, "Algebraic Connectivity of Graphs", published in the ''Czechoslovak Math Journal'' in 1973, established the use of the eigenvalues of the Laplacian matrix of a graph to create tools for measuring algebraic connectivity in algebraic graph theory. Fiedler is honored by the '' Fiedler eigenvalue'' (the second smallest eigenvalue of the graph Laplacian), with its associated '' Fiedler eigenvector'', as the names for the quantities that characterize algebraic connectivity. Since Fiedler's original contribution, this structure has become essential to large areas of research in network theory, flocking, distributed control, clustering, multi-robot applications and image segmentation. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acute Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude or quantity of these types of geometric figures and in this context an angle consists of a number and unit of measurement. Angular measure or measure of angle are sometimes used to distinguish between the measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Facet (geometry)
In geometry, a facet is a feature of a polyhedron, polytope, or related geometric structure, generally of dimension one less than the structure itself. More specifically: * In three-dimensional geometry, some authors call a facet of a polyhedron any polygon whose corners are vertices of the polyhedron, including polygons that are not ''Face (geometry), faces''. To ''facetting, facet'' a polyhedron is to find and join such facets to form the faces of a new polyhedron; this is the reciprocal process to ''stellation'' and may also be applied to higher-dimensional polytopes. * In polyhedral combinatorics and in the general theory of polytopes, a Face (geometry), face that has dimension ''n'' − 1 (an (''n'' − 1)-face or hyperface) is called a Face (geometry)#Facet, facet. In this terminology, every facet is a face. * A facet of a simplicial complex is a maximal simplex, that is a simplex that is not a face of another simplex of the complex.. For (boundary complex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
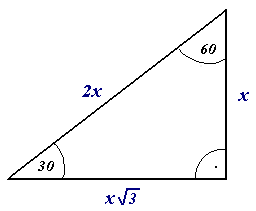
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face (geometry)
In solid geometry, a face is a flat surface (a Plane (geometry), planar region (mathematics), region) that forms part of the boundary of a solid object. For example, a cube has six faces in this sense. In more modern treatments of the geometry of polyhedra and higher-dimensional polytopes, a "face" is defined in such a way that it may have any dimension. The vertices, edges, and (2-dimensional) faces of a polyhedron are all faces in this more general sense. Polygonal face In elementary geometry, a face is a polygon on the boundary of a polyhedron. (Here a "polygon" should be viewed as including the 2-dimensional region inside it.) Other names for a polygonal face include polyhedron side and Euclidean plane ''tessellation, tile''. For example, any of the six square (geometry), squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulated Cube
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points. Applications In surveying Specifically in surveying, triangulation involves only angle measurements at known points, rather than measuring distances to the point directly as in trilateration; the use of both angles and distance measurements is referred to as triangulateration. In computer vision Computer stereo vision and optical 3D measuring systems use this principle to determine the spatial dimensions and the geometry of an item. Basically, the configuration consists of two sensors observing the item. One of the sensors is typically a digital camera device, and the other one can also be a camera or a light projector. The projection centers of the sensors and the considered point on the object's surface define a (spatial) triangle. Within this triangle, the distance between the sensors is the base ''b'' and must be known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrirectangular Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Graph
In the mathematical field of graph theory, a path graph (or linear graph) is a graph whose vertices can be listed in the order such that the edges are where . Equivalently, a path with at least two vertices is connected and has two terminal vertices (vertices of degree 1), while all others (if any) have degree 2. Paths are often important in their role as subgraphs of other graphs, in which case they are called paths in that graph. A path is a particularly simple example of a tree, and in fact the paths are exactly the trees in which no vertex has degree 3 or more. A disjoint union of paths is called a linear forest. Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See, for example, Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). As Dynkin diagrams In algebra, path graphs appear as the Dynkin diagrams of type A. As such, they classify the root system of type A and the Weyl group of type A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |