|
Resolution Proof Reduction Via Local Context Rewriting
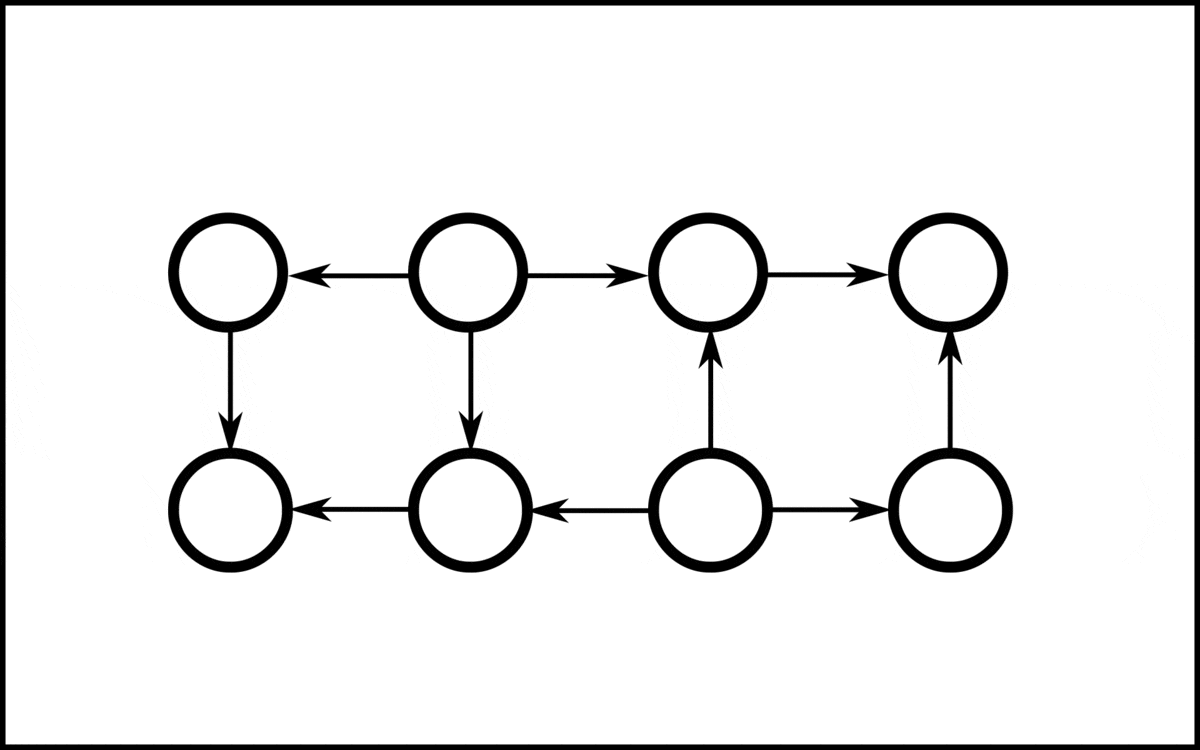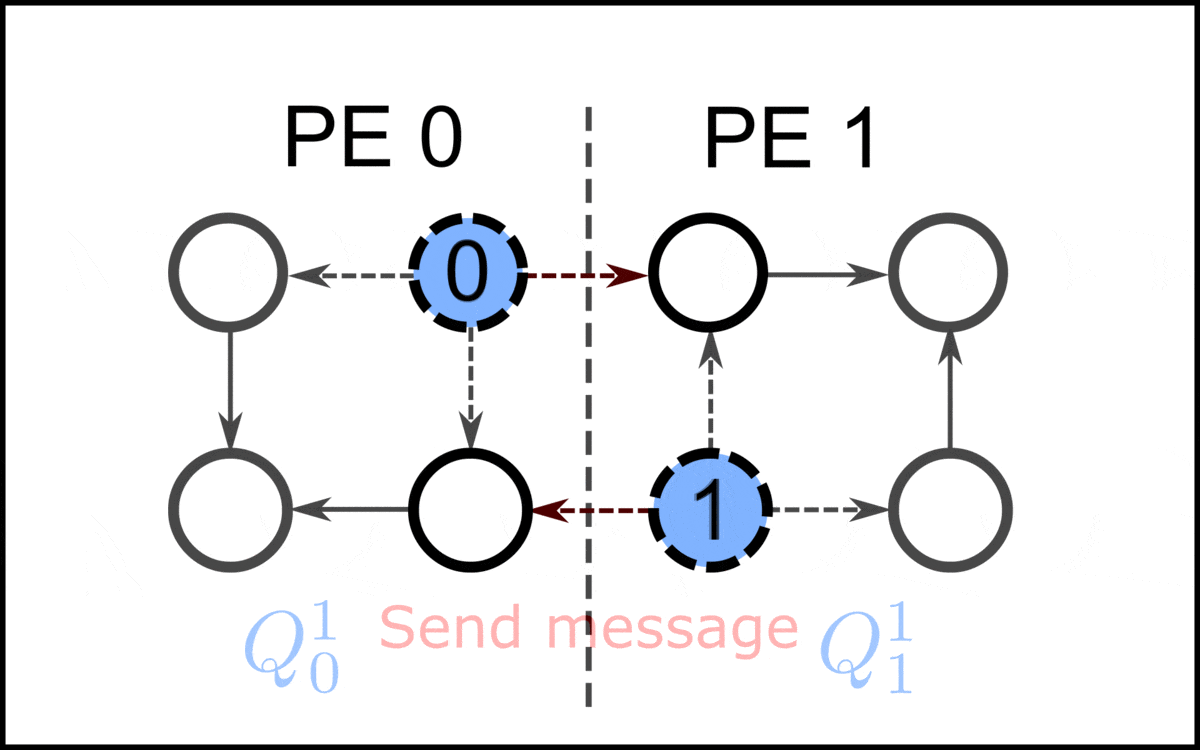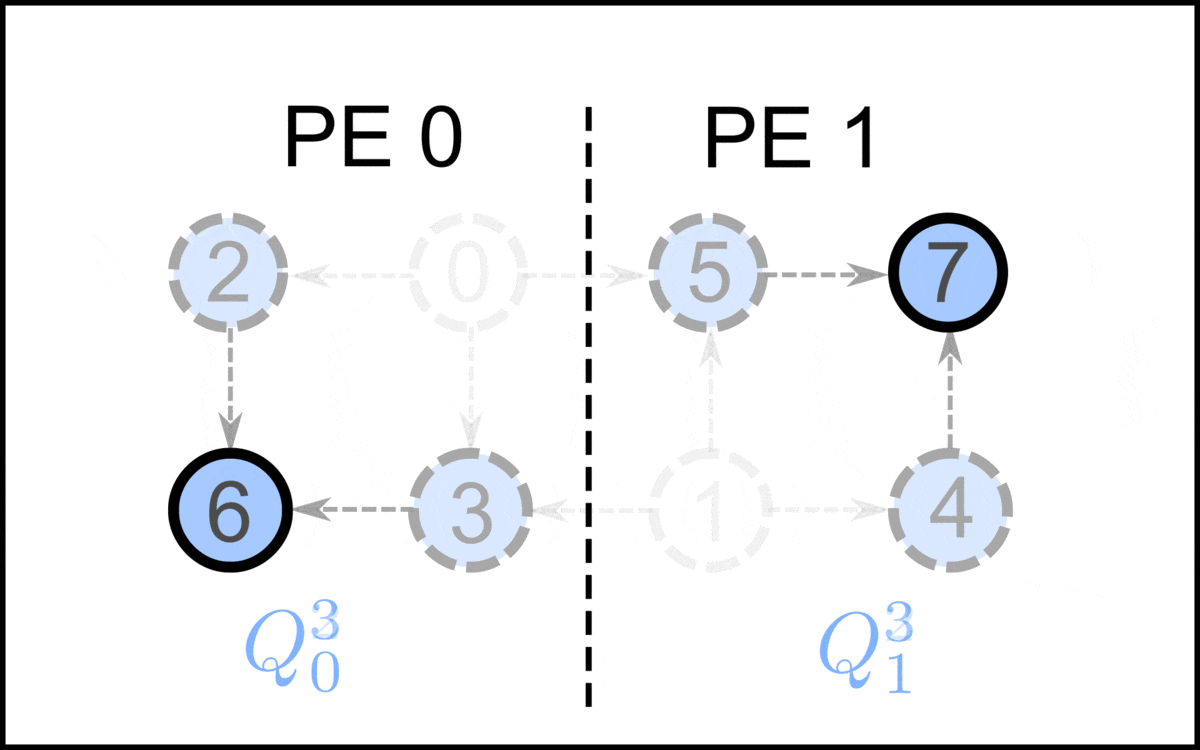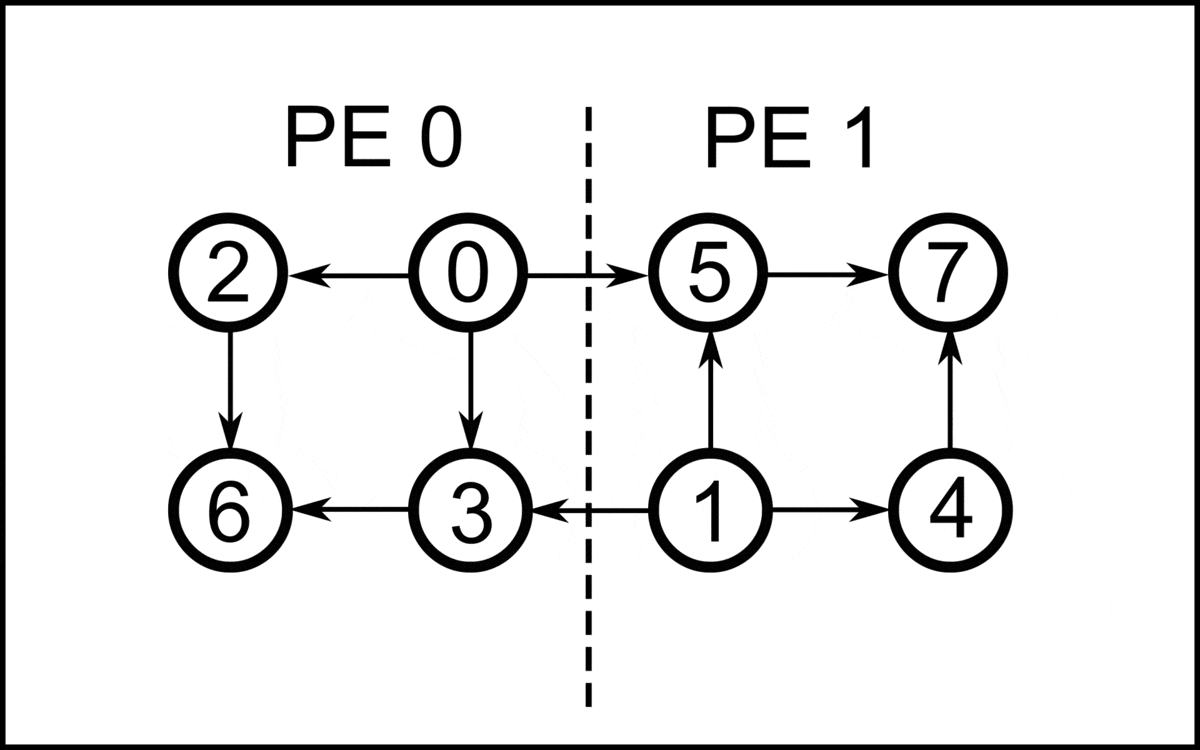
In proof theory, an area of mathematical logic, resolution proof reduction via local context rewriting is a technique for resolution proof reduction via local context rewriting.Simone, S.F.; Brutomesso, R.; Sharygina, N. "An Efficient and Flexible Approach to Resolution Proof Reduction". 6th Haifa Verification Conference, 2010. This proof compression method was presented as an algorithm named ''ReduceAndReconstruct'', that operates as a post-processing of resolution Resolution(s) may refer to: Common meanings * Resolution (debate), the statement which is debated in policy debate * Resolution (law), a written motion adopted by a deliberative body * New Year's resolution, a commitment that an individual mak ... proofs. ReduceAndReconstruct is based on a set of local proof rewriting rules that transform a subproof into an equivalent or stronger one. Each rule is defined to match a specific context. A context involves two pivots (p and q) and five clauses (\alpha, \beta, \gamma, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Theory
Proof theory is a major branchAccording to Wang (1981), pp. 3–4, proof theory is one of four domains mathematical logic, together with model theory, axiomatic set theory, and recursion theory. Barwise (1978) consists of four corresponding parts, with part D being about "Proof Theory and Constructive Mathematics". of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of the logical system. Consequently, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature. Some of the major areas of proof theory include structural proof theory, ordinal analysis, provability logic, reverse mathematics, proof mining, automated theorem proving, and proof complexity. Much research also focuses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logic
Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics. Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and analysis. In the early 20th century it was shaped by David Hilbert's program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to the program, and clarified the issues involved in proving consistency. Work in set theory s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Compression
In proof theory, an area of mathematical logic, proof compression is the problem of algorithmically compressing formal proofs. The developed algorithms can be used to improve the proofs generated by automated theorem proving tools such as SAT solvers, SMT-solvers, first-order theorem provers and proof assistants. Problem Representation In propositional logic a resolution proof of a clause \kappa from a set of clauses ''C'' is a directed acyclic graph (DAG): the input nodes are axiom inferences (without premises) whose conclusions are elements of ''C'', the resolvent nodes are resolution inferences, and the proof has a node with conclusion \kappa. The DAG contains an edge from a node \eta_ to a node \eta_ if and only if a premise of \eta_ is the conclusion of \eta_. In this case, \eta_ is a child of \eta_, and \eta_ is a parent of \eta_. A node with no children is a root. A proof compression algorithm will try to create a new DAG with fewer nodes that represents a valid proof of \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as a r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the (complement of the) Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem. The resolution rule can be traced back to Davis and Putnam (1960); however, their algorithm required trying all ground instances of the given formula. This source of combinatorial explosion was eliminated in 1965 by John Alan Robinson's syntactical unification algorithm, which allowed one to instantiate the formula during the proof "on demand" just as far as need ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Ordering
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge ''uv'' from vertex ''u'' to vertex ''v'', ''u'' comes before ''v'' in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node ''v'' is visited only after all its dependencies are visited''.'' A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications especially in ranking problems such as feedback arc set. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution Graph
Resolution(s) may refer to: Common meanings * Resolution (debate), the statement which is debated in policy debate * Resolution (law), a written motion adopted by a deliberative body * New Year's resolution, a commitment that an individual makes at New Year's Day * Dispute resolution, the settlement of a disagreement Science, technology, and mathematics Mathematics and logic * Resolution (algebra), an exact sequence in homological algebra * Resolution (logic), a rule of inference used for automated theorem proving * Standard resolution, the bar construction of resolutions in homological algebra * Resolution of singularities in algebraic geometry Measurements * Resolution (audio), a measure of digital audio quality * Resolution (electron density), the quality of an X-ray crystallography or cryo-electron microscopy data set * Angular resolution, the capability of an optical or other sensor to discern small objects * Depositional resolution, the age difference of fossils ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are sometimes instead called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heuristic
A heuristic (; ), or heuristic technique, is any approach to problem solving or self-discovery that employs a practical method that is not guaranteed to be optimal, perfect, or rational, but is nevertheless sufficient for reaching an immediate, short-term goal or approximation. Where finding an optimal solution is impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution. Heuristics can be mental shortcuts that ease the cognitive load of making a decision. Examples that employ heuristics include using trial and error, a rule of thumb or an educated guess. Heuristics are the strategies derived from previous experiences with similar problems. These strategies depend on using readily accessible, though loosely applicable, information to control problem solving in human beings, machines and abstract issues. When an individual applies a heuristic in practice, it generally performs as expected. However it can alternati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Articles With Example Pseudocode
Article often refers to: * Article (grammar), a grammatical element used to indicate definiteness or indefiniteness * Article (publishing), a piece of nonfictional prose that is an independent part of a publication Article may also refer to: Government and law * Article (European Union), articles of treaties of the European Union * Articles of association, the regulations governing a company, used in India, the UK and other countries * Articles of clerkship, the contract accepted to become an articled clerk * Articles of Confederation, the predecessor to the current United States Constitution *Article of Impeachment, a formal document and charge used for impeachment in the United States * Articles of incorporation, for corporations, U.S. equivalent of articles of association * Articles of organization, for limited liability organizations, a U.S. equivalent of articles of association Other uses * Article, an HTML element, delimited by the tags and * Article of clothing, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |