|
RSA (algorithm)
The RSA (Rivest–Shamir–Adleman) cryptosystem is a public-key cryptosystem, one of the oldest widely used for secure data transmission. The initialism "RSA" comes from the surnames of Ron Rivest, Adi Shamir and Leonard Adleman, who publicly described the algorithm in 1977. An equivalent system was developed secretly in 1973 at Government Communications Headquarters (GCHQ), the British signals intelligence agency, by the English mathematician Clifford Cocks. That system was declassified in 1997. In a public-key cryptosystem, the encryption key is public and distinct from the decryption key, which is kept secret (private). An RSA user creates and publishes a public key based on two large prime numbers, along with an auxiliary value. The prime numbers are kept secret. Messages can be encrypted by anyone via the public key, but can only be decrypted by someone who knows the private key. The security of RSA relies on the practical difficulty of factoring the product of two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ron Rivest
Ronald Linn Rivest (; born May 6, 1947) is an American cryptographer and computer scientist whose work has spanned the fields of algorithms and combinatorics, cryptography, machine learning, and election integrity. He is an Institute Professor at the Massachusetts Institute of Technology (MIT), and a member of MIT's Department of Electrical Engineering and Computer Science and its Computer Science and Artificial Intelligence Laboratory. Along with Adi Shamir and Len Adleman, Rivest is one of the inventors of the RSA algorithm. He is also the inventor of the symmetric key encryption algorithms RC2, RC4, and RC5, and co-inventor of RC6. (''RC'' stands for "Rivest Cipher".) He also devised the MD2, MD4, MD5 and MD6 cryptographic hash functions. Education Rivest earned a bachelor's degree in mathematics from Yale University in 1969, and a Ph.D. degree in computer science from Stanford University in 1974 for research supervised by Robert W. Floyd. Career At MIT, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decryption Key
A key in cryptography is a piece of information, usually a string of numbers or letters that are stored in a file, which, when processed through a cryptographic algorithm, can encode or decode cryptographic data. Based on the used method, the key can be different sizes and varieties, but in all cases, the strength of the encryption relies on the security of the key being maintained. A key's security strength is dependent on its algorithm, the size of the key, the generation of the key, and the process of key exchange. Scope The key is what is used to encrypt data from plaintext to ciphertext. There are different methods for utilizing keys and encryption. Symmetric cryptography Symmetric cryptography refers to the practice of the same key being used for both encryption and decryption. Asymmetric cryptography Asymmetric cryptography has separate keys for encrypting and decrypting. These keys are known as the public and private keys, respectively. Purpose Since the key p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Massachusetts Institute Of Technology
The Massachusetts Institute of Technology (MIT) is a Private university, private research university in Cambridge, Massachusetts, United States. Established in 1861, MIT has played a significant role in the development of many areas of modern technology and science. In response to the increasing Technological and industrial history of the United States, industrialization of the United States, William Barton Rogers organized a school in Boston to create "useful knowledge." Initially funded by a land-grant universities, federal land grant, the institute adopted a Polytechnic, polytechnic model that stressed laboratory instruction in applied science and engineering. MIT moved from Boston to Cambridge in 1916 and grew rapidly through collaboration with private industry, military branches, and new federal basic research agencies, the formation of which was influenced by MIT faculty like Vannevar Bush. In the late twentieth century, MIT became a leading center for research in compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Exponentiation
Modular exponentiation is exponentiation performed over a modulus. It is useful in computer science, especially in the field of public-key cryptography, where it is used in both Diffie–Hellman key exchange and RSA public/private keys. Modular exponentiation is the remainder when an integer (the base) is raised to the power (the exponent), and divided by a positive integer (the modulus); that is, . From the definition of division, it follows that . For example, given , and , dividing by leaves a remainder of . Modular exponentiation can be performed with a ''negative'' exponent by finding the modular multiplicative inverse of modulo using the extended Euclidean algorithm. That is: :, where and . Modular exponentiation is efficient to compute, even for very large integers. On the other hand, computing the modular discrete logarithm – that is, finding the exponent when given , , and – is believed to be difficult. This one-way function behavior makes modular e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
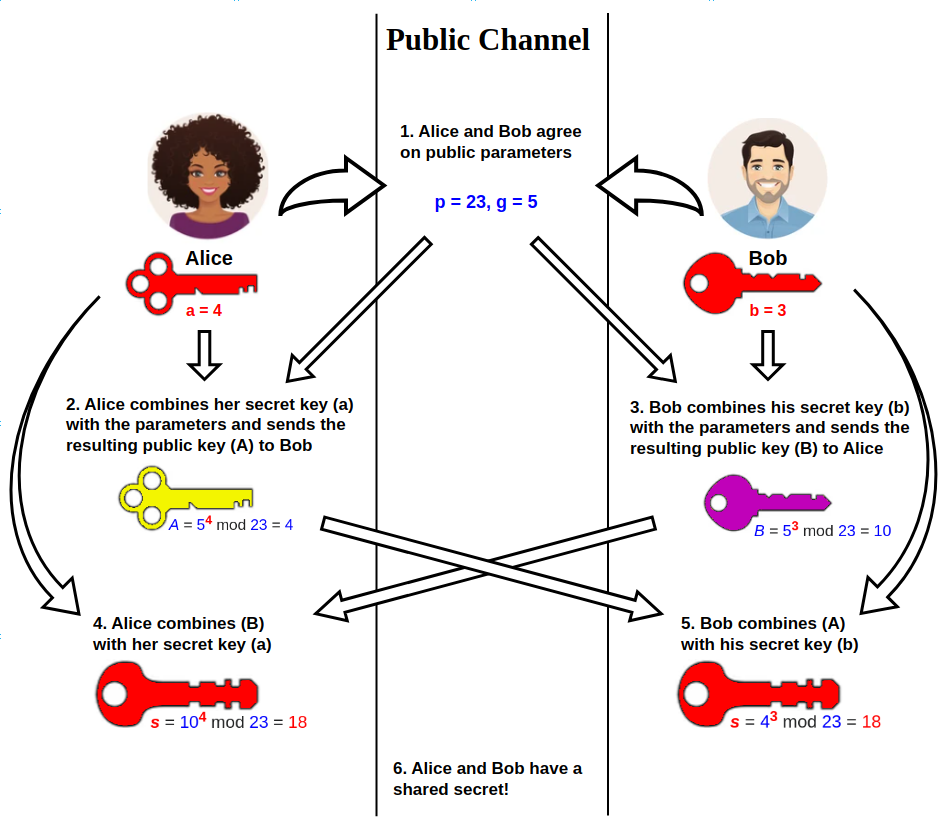
Diffie–Hellman Key Exchange
Diffie–Hellman (DH) key exchangeSynonyms of Diffie–Hellman key exchange include: * Diffie–Hellman–Merkle key exchange * Diffie–Hellman key agreement * Diffie–Hellman key establishment * Diffie–Hellman key negotiation * Exponential key exchange * Diffie–Hellman protocol * Diffie–Hellman handshake is a mathematical method of securely generating a symmetric cryptographic key over a public channel and was one of the first public-key protocols as conceived by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. DH is one of the earliest practical examples of public key exchange implemented within the field of cryptography. Published in 1976 by Diffie and Hellman, this is the earliest publicly known work that proposed the idea of a private key and a corresponding public key. Traditionally, secure encrypted communication between two parties required that they first exchange keys by some secure physical means, such as paper key lists transported by a tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Hellman
Martin Edward Hellman (born October 2, 1945) is an American cryptologist and mathematician, best known for his invention of public-key cryptography in cooperation with Whitfield Diffie and Ralph Merkle. Hellman is a longtime contributor to the computer privacy debate, and has applied risk analysis to a potential failure of nuclear deterrence. Hellman was elected a member of the National Academy of Engineering in 2002 for contributions to the theory and practice of cryptography. In 2016, he wrote a book with his wife, Dorothie Hellman, that links creating love at home to bringing peace to the planet (''A New Map for Relationships: Creating True Love at Home and Peace on the Planet''). Early life Born in New York to a Jewish family, Hellman graduated from the Bronx High School of Science. He went on to take his bachelor's degree in electrical engineering from New York University in 1966, and at Stanford University he received a master's degree and a Ph.D. in the discipline in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whitfield Diffie
Bailey Whitfield 'Whit' Diffie ForMemRS (born June 5, 1944) is an American cryptographer and mathematician and one of the pioneers of public-key cryptography along with Martin Hellman and Ralph Merkle. Diffie and Hellman's 1976 paper ''New Directions in Cryptography'' introduced a radically new method of distributing cryptographic keys, that helped solve key distribution—a fundamental problem in cryptography. Their technique became known as Diffie–Hellman key exchange. The article stimulated the almost immediate public development of a new class of encryption algorithms, the asymmetric key algorithms. After a long career at Sun Microsystems, where he became a Sun Fellow, Diffie served for two and a half years as Vice President for Information Security and Cryptography at the Internet Corporation for Assigned Names and Numbers (2010–2012). He has also served as a visiting scholar (2009–2010) and affiliate (2010–2012) at the Freeman Spogli Institute's Center for Inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adi Shamir 2009 Crop
Adi or ADI may refer to: Abbreviations * Acceptable daily intake, in health and medicine * Acting detective inspector, a type of police inspector * Africa Development Indicators, a compilation of data assembled by the World Bank * Alternating direction implicit method for solving partial differential equations * Ángeles del Infierno, a Spanish heavy metal band * Anti-detonant injection, another name for water injection in internal combustion engines * Approved Driving Instructor, a qualified UK car driver trainer * Area of dominant influence, term used by Arbitron in media marketing * Authorised deposit-taking institution, a corporation authorised under the Australian ''Commonwealth Banking Act 1959'' * Autism Diagnostic Interview, a parent interview used to aid diagnosis of autism Aviation * Aerodynamics Inc., a small airline in the US * Aircraft Designs Inc, an aircraft design firm in Monterey, California * IATA airport code for Arandis Airport in Erongo Region, Na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric-key Algorithm
Symmetric-key algorithms are algorithms for cryptography that use the same cryptographic keys for both the encryption of plaintext and the decryption of ciphertext. The keys may be identical, or there may be a simple transformation to go between the two keys. The keys, in practice, represent a shared secret between two or more parties that can be used to maintain a private information link. The requirement that both parties have access to the secret key is one of the main drawbacks of symmetric-key encryption, in comparison to public-key encryption (also known as asymmetric-key encryption). However, symmetric-key encryption algorithms are usually better for bulk encryption. With exception of the one-time pad they have a smaller key size, which means less storage space and faster transmission. Due to this, asymmetric-key encryption is often used to exchange the secret key for symmetric-key encryption. Types Symmetric-key encryption can use either stream ciphers or block ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Shor
Peter Williston Shor (born August 14, 1959) is an American theoretical computer scientist known for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical computer. He has been a professor of applied mathematics at the Massachusetts Institute of Technology (MIT) since 2003. Early life and education Shor was born on August 14, 1959, in New York City, to Joan Bopp Shor and S. W. Williston Shor.Joan Shor Obituary He grew up in Washington, D.C. and |
RSA Problem
In cryptography, the RSA problem summarizes the task of performing an RSA private-key operation given only the public key. The RSA algorithm raises a ''message'' to an '' exponent'', modulo a composite number ''N'' whose factors are not known. Thus, the task can be neatly described as finding the ''e''th roots of an arbitrary number, modulo N. For large RSA key sizes (in excess of 1024 bits), no efficient method for solving this problem is known; if an efficient method is ever developed, it would threaten the current or eventual security of RSA-based cryptosystems—both for public-key encryption and digital signatures. More specifically, the RSA problem is to efficiently compute ''P'' given an RSA public key (''N'', ''e'') and a ciphertext ''C'' ≡ ''P'' ''e'' (mod ''N''). The structure of the RSA public key requires that ''N'' be a large semiprime (i.e., a product of two large prime numbers), that 2 < ''e'' < ''N'', that ''e'' be |
Factoring Problem
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |