|
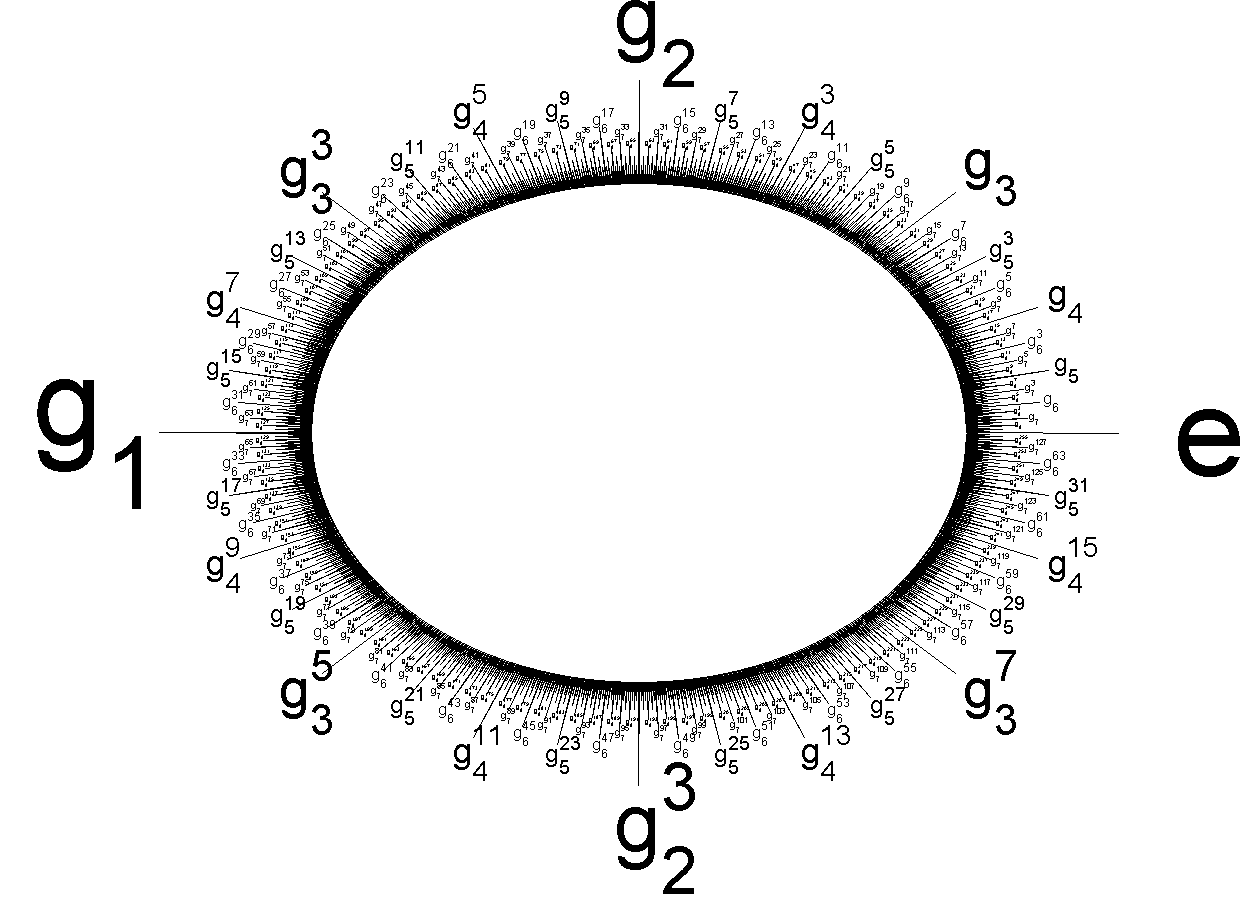
Prüfer Group
In mathematics, specifically in group theory, the Prüfer ''p''-group or the ''p''-quasicyclic group or ''p''∞-group, Z(''p''∞), for a prime number ''p'' is the unique ''p''-group in which every element has ''p'' different ''p''-th roots. The Prüfer ''p''-groups are countable abelian groups that are important in the classification of infinite abelian groups: they (along with the group of rational numbers) form the smallest building blocks of all divisible groups. The groups are named after Heinz Prüfer, a German mathematician of the early 20th century. Constructions of Z(''p''∞) The Prüfer ''p''-group may be identified with the subgroup of the circle group, U(1), consisting of all ''p''''n''-th roots of unity as ''n'' ranges over all non-negative integers: :\mathbf(p^\infty)=\ = \.\; The group operation here is the multiplication of complex numbers. There is a presentation :\mathbf(p^\infty) = \langle\, g_1, g_2, g_3, \ldots \mid g_1^p = 1, g_2^p = g_1, g_3^p = g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prüfer
Pruefer or Prüfer is a surname of German derivation, and may refer to: * Heinz Prüfer Ernst Paul Heinz Prüfer (10 November 1896 – 7 April 1934) was a German Jewish mathematician born in Wilhelmshaven. His major contributions were on abelian groups, graph theory, algebraic numbers, knot theory and Sturm–Liouville theory. In 1 ..., German Jewish mathematician (1896-1934) * Kevin Prufer, American poet (1969) * Gustav Franz Pruefer, American Music instrument inventor (1861-1951) See also * Prüffer German-language surnames Jewish surnames {{Reflist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Space
In topology and related branches of mathematics, a Hausdorff space ( , ), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each which are disjoint from each other. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" (T2) is the most frequently used and discussed. It implies the uniqueness of limits of sequences, nets, and filters. Hausdorff spaces are named after Felix Hausdorff, one of the founders of topology. Hausdorff's original definition of a topological space (in 1914) included the Hausdorff condition as an axiom. Definitions Points x and y in a topological space X can be '' separated by neighbourhoods'' if there exists a neighbourhood U of x and a neighbourhood V of y such that U and V are disjoint (U\cap V=\varnothing). X is a Hausdorff space if any two distinct points in X are separated by neighbourhoods. This condition is the third separ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artinian Group
In mathematics, specifically group theory, a subgroup series of a group G is a chain of subgroups: :1 = A_0 \leq A_1 \leq \cdots \leq A_n = G where 1 is the trivial subgroup. Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups. A subgroup series is used in the subgroup method. Subgroup series are a special example of the use of filtrations in abstract algebra. Definition Normal series, subnormal series A subnormal series (also normal series, normal tower, subinvariant series, or just series) of a group ''G'' is a sequence of subgroups, each a normal subgroup of the next one. In a standard notation :1 = A_0\triangleleft A_1\triangleleft \cdots \triangleleft A_n = G. There is no requirement made that ''A''''i'' be a normal subgroup of ''G'', only a normal subgroup of ''A''''i'' +1. The quotient groups ''A''''i'' +1/''A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Module (mathematics)
In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a ring. The concept of ''module'' generalizes also the notion of abelian group, since the abelian groups are exactly the modules over the ring of integers. Like a vector space, a module is an additive abelian group, and scalar multiplication is distributive over the operation of addition between elements of the ring or module and is compatible with the ring multiplication. Modules are very closely related to the representation theory of groups. They are also one of the central notions of commutative algebra and homological algebra, and are used widely in algebraic geometry and algebraic topology. Introduction and definition Motivation In a vector space, the set of scalars is a field and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scalars need only be a ring, so the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. The '' transfinite'' cardinal numbers, often denoted using the Hebrew symbol \aleph ( aleph) followed by a subscript, describe the sizes of infinite sets. Cardinality is defined in terms of bijective functions. Two sets have the same cardinality if, and only if, there is a one-to-one correspondence (bijection) between the elements of the two sets. In the case of finite sets, this agrees with the intuitive notion of size. In the case of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor shows that it is possible for infinite sets to have different cardinalities, and in particular the cardinality of the set of real numbers is greater than the cardinality of the set of natural numbers. It is also po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisible Group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an ''n''th multiple for each positive integer ''n''. Divisible groups are important in understanding the structure of abelian groups, especially because they are the injective abelian groups. Definition An abelian group (G, +) is divisible if, for every positive integer n and every g \in G, there exists y \in G such that ny=g. An equivalent condition is: for any positive integer n, nG=G, since the existence of y for every n and g implies that n G\supseteq G, and the other direction n G\subseteq G is true for every group. A third equivalent condition is that an abelian group G is divisible if and only if G is an injective object in the category of abelian groups; for this reason, a divisible group is sometimes called an injective group. An abelian group is p-divisible for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Cyclic Group
In mathematics, a locally cyclic group is a group (''G'', *) in which every finitely generated subgroup is cyclic group, cyclic. Some facts * Every cyclic group is locally cyclic, and every locally cyclic group is abelian group, abelian. * Every finitely-generated locally cyclic group is cyclic. * Every subgroup and quotient group of a locally cyclic group is locally cyclic. * Every homomorphism, homomorphic image of a locally cyclic group is locally cyclic. * A group is locally cyclic if and only if every pair of elements in the group generates a cyclic group. * A group is locally cyclic if and only if its lattice of subgroups is distributive lattice, distributive . * The torsion-free rank of a locally cyclic group is 0 or 1. * The endomorphism ring of a locally cyclic group is commutative ring, commutative. Examples of locally cyclic groups that are not cyclic Examples of abelian groups that are not locally cyclic * The additive group of real numbers (R, +); the subgroup genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subdirectly Irreducible Algebra
In the branch of mathematics known as universal algebra (and in its applications), a subdirectly irreducible algebra is an algebra that cannot be factored as a subdirect product of "simpler" algebras. Subdirectly irreducible algebras play a somewhat analogous role in algebra to primes in number theory. Definition A universal algebra ''A'' is said to be subdirectly irreducible when ''A'' has more than one element, and when any subdirect representation of ''A'' includes (as a factor) an algebra isomorphic to ''A'', with the isomorphism being given by the projection map. Examples * The two-element chain, as either a Boolean algebra, a Heyting algebra, a lattice, or a semilattice, is subdirectly irreducible. In fact, the two-element chain is the only subdirectly irreducible distributive lattice. * Any finite chain with two or more elements, as a Heyting algebra, is subdirectly irreducible. (This is not the case for chains of three or more elements as either lattices or semila ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Sum
The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. To see how the direct sum is used in abstract algebra, consider a more elementary kind of structure, the abelian group. The direct sum of two abelian groups A and B is another abelian group A\oplus B consisting of the ordered pairs (a,b) where a \in A and b \in B. To add ordered pairs, we define the sum (a, b) + (c, d) to be (a + c, b + d); in other words addition is defined coordinate-wise. For example, the direct sum \Reals \oplus \Reals , where \Reals is real coordinate space, is the Cartesian plane, \R ^2 . A similar process can be used to form the direct sum of two vector spaces or two modules. We can also form direct sums with any finite number of summands, for example A \oplus B \oplus C, provided A, B, and C are the same kinds of algebraic structures (e.g., all abelian groups, or all vector sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indecomposable Module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules. Jacobson (2009), p. 111. Indecomposable is a weaker notion than simple module (which is also sometimes called irreducible module): simple means "no proper submodule" N < M, while indecomposable "not expressible as ". A direct sum of indecomposables is called completely decomposable; this is weaker than being semisimple, which is a direct sum of simple modules. A direct sum decomposition of a module into indecomposable modules is called an indecomposa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frattini Subgroup
In mathematics, particularly in group theory, the Frattini subgroup \Phi(G) of a group is the intersection of all maximal subgroups of . For the case that has no maximal subgroups, for example the trivial group or a Prüfer group, it is defined by \Phi(G)=G. It is analogous to the Jacobson radical in the theory of rings, and intuitively can be thought of as the subgroup of "small elements" (see the "non-generator" characterization below). It is named after Giovanni Frattini, who defined the concept in a paper published in 1885. Some facts * \Phi(G) is equal to the set of all non-generators or non-generating elements of . A non-generating element of is an element that can always be removed from a generating set; that is, an element ''a'' of such that whenever is a generating set of containing ''a'', X \setminus \ is also a generating set of . * \Phi(G) is always a characteristic subgroup of ; in particular, it is always a normal subgroup of . * If is finite, then \P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximal Subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra. In group theory, a maximal subgroup ''H'' of a group ''G'' is a proper subgroup, such that no proper subgroup ''K'' contains ''H'' strictly. In other words, ''H'' is a maximal element of the partially ordered set of subgroups of ''G'' that are not equal to ''G''. Maximal subgroups are of interest because of their direct connection with primitive permutation representations of ''G''. They are also much studied for the purposes of finite group theory: see for example Frattini subgroup, the intersection of the maximal subgroups. In semigroup theory, a maximal subgroup of a semigroup ''S'' is a subgroup (that is, a subsemigroup which forms a group under the semigroup operation) of ''S'' which is not properly contained in another subgroup of ''S''. Notice that, here, there is no requirement that a maximal subgroup be proper, so if ''S'' is in fact a group then its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |