|
Pauli Equation
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non- relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927. Equation For a particle of mass m and electric charge q, in an electromagnetic field described by the magnetic vector potential \mathbf and the electric scalar potential \phi, the Pauli equation reads: Here \boldsymbol = (\sigma_x, \sigma_y, \sigma_z) are the Pauli operators collected into a vector for convenience, and \mathbf = -i\hbar \nabla is the momentum operator in position representation. The state of the system, , \psi\rangle (written in Dirac notation), can be considered as a tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves ( wave–particle duality); and there are lim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bohr Magneton
In atomic physics, the Bohr magneton (symbol ) is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by its orbital or spin angular momentum. The Bohr magneton, in SI units is defined as \mu_\mathrm = \frac , And in Gaussian CGS units: \mu_\mathrm = \frac , where * is the elementary charge, * is the reduced Planck constant, * is the electron rest mass, * is the speed of light. History The idea of elementary magnets is due to Walther Ritz (1907) and Pierre Weiss. Already before the Rutherford model of atomic structure, several theorists commented that the magneton should involve the Planck constant ''h''. By postulating that the ratio of electron kinetic energy to orbital frequency should be equal to ''h'', Richard Gans computed a value that was twice as large as the Bohr magneton in September 1911. At the First Solvay Conference in November that year, Paul Langevin obtained a e\hbar/(12m_\mathrm). Langevin assumed tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeeman Effect
The Zeeman effect (; ) is the effect of splitting of a spectral line into several components in the presence of a static magnetic field. It is named after the Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel prize for this discovery. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field. Also similar to the Stark effect, transitions between different components have, in general, different intensities, with some being entirely forbidden (in the dipole approximation), as governed by the selection rules. Since the distance between the Zeeman sub-levels is a function of magnetic field strength, this effect can be used to measure magnetic field strength, e.g. that of the Sun and other stars or in laboratory plasmas. The Zeeman effect is very important in applications such as nuclear magnetic resonance spectroscopy, electron spin resonance spectroscopy, magnetic resona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
G-factor (physics)
A ''g''-factor (also called ''g'' value or dimensionless magnetic moment) is a dimensionless quantity that characterizes the magnetic moment and angular momentum of an atom, a particle or the nucleus. It is essentially a proportionality constant that relates the different observed magnetic moments ''μ'' of a particle to their angular momentum quantum numbers and a unit of magnetic moment (to make it dimensionless), usually the Bohr magneton or nuclear magneton. Definition Dirac particle The spin magnetic moment of a charged, spin-1/2 particle that does not possess any internal structure (a Dirac particle) is given by \boldsymbol \mu = g \mathbf S , where ''μ'' is the spin magnetic moment of the particle, ''g'' is the ''g''-factor of the particle, ''e'' is the elementary charge, ''m'' is the mass of the particle, and S is the spin angular momentum of the particle (with magnitude ''ħ''/2 for Dirac particles). Baryon or nucleus Protons, neutrons, nuclei and other compos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular momen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. When the position operator is considered with a wide enough domain (e.g. the space of tempered distributions), its eigenvalues are the possible position vectors of the particle. In one dimension, if by the symbol , x \rangle we denote the unitary eigenvector of the position operator corresponding to the eigenvalue x, then, , x \rangle represents the state of the particle in which we know with certainty to find the particle itself at position x. Therefore, denoting the position operator by the symbol X in the literature we find also other symbols for the position operator, for instance Q (from Lagrangian mechanics), \hat \mathrm x and so on we can write X, x\rangle = x , x\rangle, for every real position x. One possible realization of the unitary state with position x is the Dirac delta (function) distribution centered at the position x, often denoted by \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
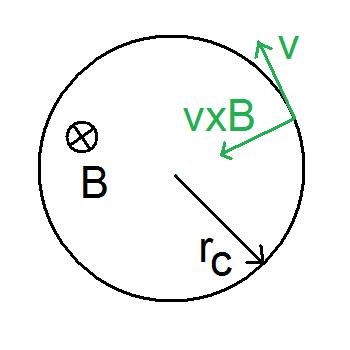
Landau Quantization
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau. Landau quantization is directly responsible for the electronic susceptibility of metals, known as Landau diamagnetism. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as De Haas–Van Alphen and Shubnikov–de Haas effects. Landau quantization is a key ingredient to explain the integer quantum Hall effect. Derivation Consider a system of non-interacting particles with charge and spin confined to an area in the plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Momentum
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone–von Neumann theorem and canonical commutation relations for details. As Hamiltonian mechanics are generalized by symplectic geometry and canonical transformations are generalized by contact transformations, so the 19th century definition of canonical coordinates in classical mechanics may be generalized to a more abstract 20th century definition of coordinates on the cotangent bundle of a manifold (the mathematical notion of phase space). Definition in classical mechanics In classical mechanics, canonical coordinates are coordinates q^i and p_i in phase space that are used in the Hamiltonian formalism. The canonical coordinates satisfy the fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics, quantum f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Coupling
In analytical mechanics and quantum field theory, minimal coupling refers to a coupling between fields which involves only the charge distribution and not higher multipole moments of the charge distribution. This minimal coupling is in contrast to, for example, Pauli coupling, which includes the magnetic moment of an electron directly in the Lagrangian. Electrodynamics In electrodynamics, minimal coupling is adequate to account for all electromagnetic interactions. Higher moments of particles are consequences of minimal coupling and non-zero spin. Non-relativistic charged particle in an electromagnetic field In Cartesian coordinates, the Lagrangian of a non-relativistic classical particle in an electromagnetic field is (in SI Units): : \mathcal = \sum_i \tfrac m \dot_i^2 + \sum_i q \dot_i A_i - q \varphi where is the electric charge of the particle, is the electric scalar potential, and the are the components of the magnetic vector potential that may all explicitly dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |