|
N-sphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, called the ''center''. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit -sphere or simply the -sphere for brevity. In terms of the standard norm, the -sphere is defined as : S^n = \left\ , and an -sphere of radius can be defined as : S^n(r) = \left\ . The dimension of -sphere is , and must not be confused with the dimension of the Euclidean space in which it is naturally embedded. An -sphere is the surface or boundary of an -dimensional ball. In particular: *the pair of points at the ends of a (one-dimensional) line segment is a 0-sphere, *a circle, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere (or 2-sphere, a two-dimensional surface), the boundary of a ball in four dimensions is a 3-sphere (an object with three dimensions). A 3-sphere is an example of a 3-manifold and an ''n''-sphere. Definition In coordinates, a 3-sphere with center and radius is the set of all points in real, 4-dimensional space () such that :\sum_^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted : :S^3 = \left\. It is often convenient to regard as the space with 2 complex dimensions () or the quaternions (). The unit 3-sphere is then given by :S^3 = \left\ or :S^3 = \left\. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
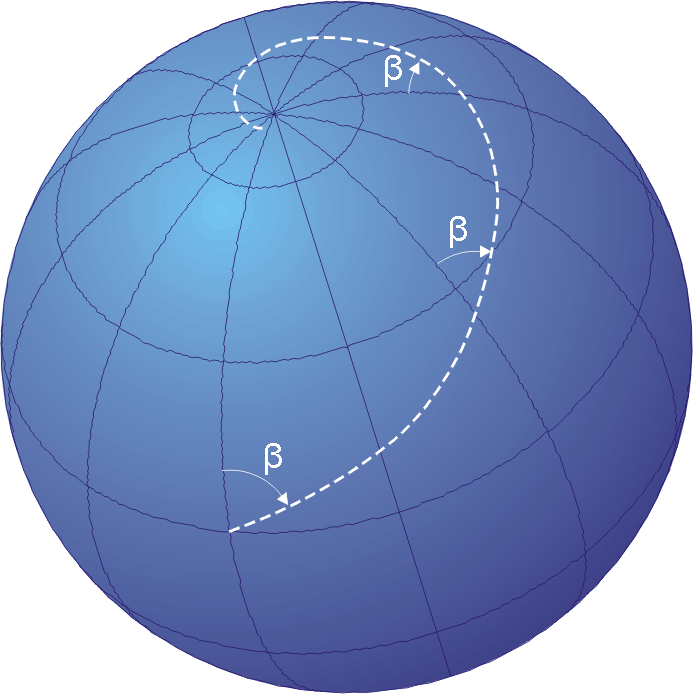
Hypersphere Coord
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, called the ''center''. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit -sphere or simply the -sphere for brevity. In terms of the standard norm, the -sphere is defined as : S^n = \left\ , and an -sphere of radius can be defined as : S^n(r) = \left\ . The dimension of -sphere is , and must not be confused with the dimension of the Euclidean space in which it is naturally embedded. An -sphere is the surface or boundary of an -dimensional ball. In particular: *the pair of points at the ends of a (one-dimensional) line segment is a 0-sphere, *a circle, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance of a vector from the origin is a norm, called the Euclidean norm, or 2-norm, which may also be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm, but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meanings. It may be a synonym of "seminorm". A pseudonorm may satisfy the same axioms as a norm, with the equality replaced by an inequality "\,\leq\," in the homogeneity axiom. It can also re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2-sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphere's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1-sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphere's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simply Connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the space) into any other such path while preserving the two endpoints in question. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit circle and closed unit disk in the Euclidean plane respectively. An equivalent formulation is this: X is simply connected if and only if it is path-connected, and whenev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ball (mathematics)
In mathematics, a ball is the solid figure bounded by a ''sphere''; it is also called a solid sphere. It may be a closed ball (including the boundary points that constitute the sphere) or an open ball (excluding them). These concepts are defined not only in three-dimensional Euclidean space but also for lower and higher dimensions, and for metric spaces in general. A ''ball'' in dimensions is called a hyperball or -ball and is bounded by a ''hypersphere'' or ()-sphere. Thus, for example, a ball in the Euclidean plane is the same thing as a disk, the area bounded by a circle. In Euclidean 3-space, a ball is taken to be the volume bounded by a 2-dimensional sphere. In a one-dimensional space, a ball is a line segment. In other contexts, such as in Euclidean geometry and informal use, ''sphere'' is sometimes used to mean ''ball''. In the field of topology the closed n-dimensional ball is often denoted as B^n or D^n while the open n-dimensional ball is \operatorname B^n or \ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Wireframe
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphere's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position (geometry), position of an element (i.e., Point (mathematics), point). This is the informal meaning of the term dimension. In mathematics, a tuple of Real number, numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e.g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume Form
In mathematics, a volume form or top-dimensional form is a differential form of degree equal to the differentiable manifold dimension. Thus on a manifold M of dimension n, a volume form is an n-form. It is an element of the space of sections of the line bundle \textstyle^n(T^*M), denoted as \Omega^n(M). A manifold admits a nowhere-vanishing volume form if and only if it is orientable. An orientable manifold has infinitely many volume forms, since multiplying a volume form by a function yields another volume form. On non-orientable manifolds, one may instead define the weaker notion of a density. A volume form provides a means to define the integral of a function on a differentiable manifold. In other words, a volume form gives rise to a measure with respect to which functions can be integrated by the appropriate Lebesgue integral. The absolute value of a volume form is a volume element, which is also known variously as a ''twisted volume form'' or ''pseudo-volume form''. It als ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |