|
Multidimensional Transform
In mathematical analysis and applications, multidimensional transforms are used to analyze the frequency content of signals in a domain of two or more dimensions. Multidimensional Fourier transform One of the more popular multidimensional transforms is the Fourier transform, which converts a signal from a time/space domain representation to a frequency domain representation.Smith, W. Handbook of Real-Time Fast Fourier Transforms:Algorithms to Product Testing, Wiley_IEEE Press, edition 1, pages 73–80, 1995 The discrete-domain multidimensional Fourier transform (FT) can be computed as follows: : F(w_1,w_2,\dots,w_m) = \sum_^\infty \sum_^\infty \cdots \sum_^\infty f(n_1,n_2,\dots,n_m) e^ where ''F'' stands for the multidimensional Fourier transform, ''m'' stands for multidimensional dimension. Define ''f'' as a multidimensional discrete-domain signal. The inverse multidimensional Fourier transform is given by : f(n_1,n_2,\dots,n_m) = \left(\frac\right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidimensional Modulation
Multidimensional modulation (MD modulation) is modifying or multiplying an MD signal (typically sinusoidal and referred to as the carrier signal) with another signal that carries some information or message. In the frequency domain, the signal is moved from one frequency to another. if then Typically the carrier signal is a sinusoidal signal and in various applications. The figures below illustrate a quick example of a 2-D modulation. The original signal from () is modulated with a sinusoidal signal to get (). The equations () and () are the real and the imaginary components of the modulated signal. Background/Motivation The MD modulation is one of the properties of the Multidimensional_transform#Multidimensional_Fourier_transform, Multidimensional Fourier Transform. MD Fourier Transform (FT) Fourier Transform (FT) of multi-dimensional (MD) signal or system is the transform of the MD signal or system that decomposes it into its frequency components. Essentially, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
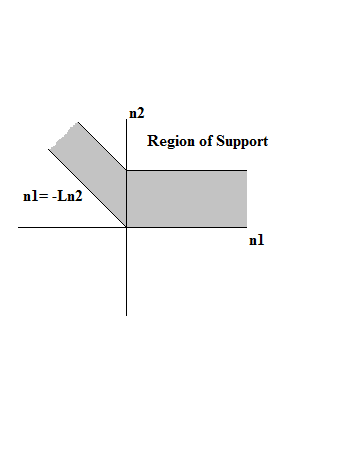
2D Z-transform
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.Siamak Khatibi, “Multidimensional Signal Processing: Lecture 11”, BLEKINGE INSTITUTE OF TECHNOLOGY, PowerPoint Presentation. The 2D Z-transform is defined by :X_z(z_1,z_2) = \sum_^\sum_^ x(n_1,n_2) z_1^ z_2^ where n_1,n_2 are integers and z_1,z_2 are represented by the complex numbers: :z_1 = Ae^ = A(\cos+j\sin)\, :z_2 = Be^ = B(\cos+j\sin)\, The 2D Z-transform is a generalized version of the 2D Fourier transform. It converges for a much wider class of sequences, and is a helpful tool in allowing one to draw conclusions on system characteristics such as BIBO stability. It is also used to determine the connection between the input and output of a linear shift-invariant system, such as mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete-time Fourier Transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values. The DTFT is often used to analyze samples of a continuous function. The term ''discrete-time'' refers to the fact that the transform operates on discrete data, often samples whose interval has units of time. From uniformly spaced samples it produces a function of frequency that is a periodic summation of the continuous Fourier transform of the original continuous function. In simpler terms, when you take the DTFT of regularly-spaced samples of a continuous signal, you get repeating (and possibly overlapping) copies of the signal's frequency spectrum, spaced at intervals corresponding to the sampling frequency. Under certain theoretical conditions, described by the sampling theorem, the original continuous function can be recovered perfectly from the DTFT and thus from the original discrete samples. The DTFT itself is a continuous functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function (mathematics), function as input then outputs another function that describes the extent to which various Frequency, frequencies are present in the original function. The output of the transform is a complex number, complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the Operation (mathematics), mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical Chord (music), chord into the sound intensity, intensities of its constituent Pitch (music), pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the #Uncertainty principle, uncerta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectral energy distribution that would b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy Encoding
In information theory, an entropy coding (or entropy encoding) is any lossless data compression method that attempts to approach the lower bound declared by Shannon's source coding theorem, which states that any lossless data compression method must have an expected code length greater than or equal to the entropy of the source. More precisely, the source coding theorem states that for any source distribution, the expected code length satisfies \operatorname E_ ell(d(x))\geq \operatorname E_ \log_b(P(x))/math>, where \ell is the function specifying the number of symbols in a code word, d is the coding function, b is the number of symbols used to make output codes and P is the probability of the source symbol. An entropy coding attempts to approach this lower bound. Two of the most common entropy coding techniques are Huffman coding and arithmetic coding. If the approximate entropy characteristics of a data stream are known in advance (especially for signal compression), a simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantization (signal Processing)
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set (often a continuous set) to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms. The difference between an input value and its quantized value (such as round-off error) is referred to as quantization error, noise or distortion. A device or algorithm function, algorithmic function that performs quantization is called a quantizer. An analog-to-digital converter is an example of a quantizer. Example For example, Rounding#Round half up, rounding a real number x to the nearest integer value forms a very basic type of q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Video Compression
In information theory, data compression, source coding, or bit-rate reduction is the process of encoding information using fewer bits than the original representation. Any particular compression is either lossy or lossless. Lossless compression reduces bits by identifying and eliminating Redundancy (information theory), statistical redundancy. No information is lost in lossless compression. Lossy compression reduces bits by removing unnecessary or less important information. Typically, a device that performs data compression is referred to as an encoder, and one that performs the reversal of the process (decompression) as a decoder. The process of reducing the size of a data file is often referred to as data compression. In the context of data transmission, it is called source coding: encoding is done at the source of the data before it is stored or transmitted. Source coding should not be confused with channel coding, for error detection and correction or line coding, the means ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theora
Theora is a free lossy video compression format. It was developed by the Xiph.Org Foundation and distributed without licensing fees alongside their other free and open media projects, including the Vorbis audio format and the Ogg container. The libtheora video codec is the reference implementation of the Theora video compression format developed by the Xiph.Org Foundation. Theora was derived from the formerly proprietary VP3 codec, released into the public domain by On2 Technologies. It is broadly comparable in design and bitrate efficiency to MPEG-4 Part 2, early versions of Windows Media Video, and RealVideo while it lacked some of the features present in some of these other codecs. It is comparable in open standards philosophy to the BBC's Dirac codec. Theora was named after Theora Jones, Edison Carter's Controller on the '' Max Headroom'' television program. Technical details Theora is a variable-bitrate, DCT-based video compression scheme. Like most ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daala
Daala is a video coding format under development by the Xiph.Org Foundation under the lead of Timothy B. Terriberry mainly sponsored by the Mozilla Corporation. Like Theora and Opus, Daala is available free of any royalties and its reference implementation is being developed as free and open-source software. The name is taken from the fictional character of Admiral Natasi Daala from the ''Star Wars'' universe. The reference implementation is written in C and published, together with its source code, as free software under the terms of a BSD-like license. Software patents are being filed for techniques used in and developed for Daala. Those patents are freely licensed to everybody to use for any purpose. However, the patent holders reserve the right to use them to counter patent infringement lawsuits filed by others. Since June 20, 2013, the development is accompanied by a series of sporadically published posts on the underlying technology on the website of the Xiph.Org Fou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DV (video Format)
DV (from ''Digital Video'') is a family of codecs and Videotape, tape formats used for storing digital video, launched in 1995 by a consortium of camcorder, video camera manufacturers led by Sony and Panasonic. It includes the recording or cassette formats DV, MiniDV, HDV, DVCAM, DVCPro, DVCPro50, DVCProHD, Digital8, and Digital-S. DV has been used primarily for video recording with camcorders in the amateur and professional sectors. DV was designed to be a standard for home video using digital data instead of Analog video, analog. Compared to the analog 8 mm video format, Video8/Hi8, VHS-C and VHS formats, DV features a higher video resolution (on par with professional-grade Digital Betacam); it records uncompressed 16-bit Pulse-code modulation, PCM audio like Compact Disc Digital Audio, CD. The most popular tape format using a DV codec was MiniDV; these cassettes measured just 6.35 mm/¼ inch, making it ideal for video cameras and rendering older analog formats obsolete. In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |