|
Molecular Vibration
A molecular vibration is a Periodic function, periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The infrared spectroscopy correlation table, typical vibrational frequencies range from less than 1013 hertz, Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has vibrational mode, normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. A molecular vibration is excited when the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
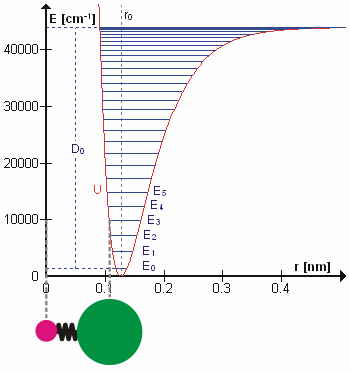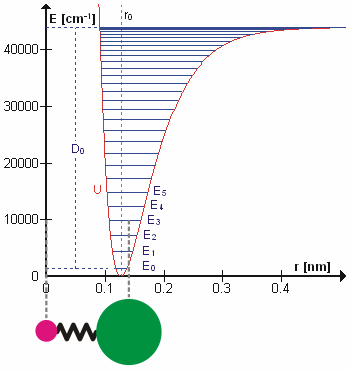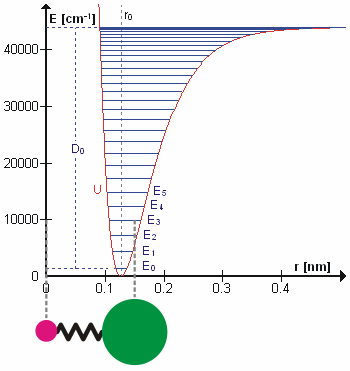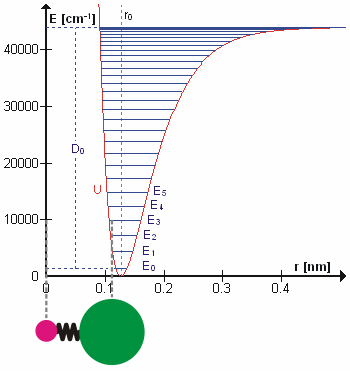
Morse/Long-range Potential
The Morse/Long-range potential (MLR potential) is an interatomic interaction model for the potential energy of a diatomic molecule. Due to the simplicity of the regular Morse potential (it only has three adjustable parameters), it is very limited in its applicability in modern spectroscopy. The MLR potential is a modern version of the Morse potential which has the correct theoretical long-range form of the potential naturally built into it. It has been an important tool for spectroscopists to represent experimental data, verify measurements, and make predictions. It is useful for its extrapolation capability when data for certain regions of the potential are missing, its ability to predict energies with accuracy often better than the most sophisticated ''ab initio'' techniques, and its ability to determine precise empirical values for physical parameters such as the dissociation energy, equilibrium bond length, and long-range constants. Cases of particular note include: # the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Translation (geometry)
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same Distance geometry, distance in a given direction (geometry), direction. A translation can also be interpreted as the addition of a constant vector space, vector to every point, or as shifting the Origin (mathematics), origin of the coordinate system. In a Euclidean space, any translation is an isometry. As a function If \mathbf is a fixed vector, known as the ''translation vector'', and \mathbf is the initial position of some object, then the translation function T_ will work as T_(\mathbf)=\mathbf+\mathbf. If T is a translation, then the image (mathematics), image of a subset A under the function (mathematics), function T is the translate of A by T . The translate of A by T_ is often written as A+\mathbf . Application in classical physics In classical physics, translational motion is movement that changes the Position (geometry), positio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the chosen parameterization of a physical system. More formally, given a parameterization of a physical system, the number of degrees of freedom is the smallest number n of parameters whose values need to be known in order to always be possible to determine the values of ''all'' parameters in the chosen parameterization. In this case, any set of n such parameters are called degrees of freedom. The location of a particle in three-dimensional space requires three Coordinate system, position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. So, if the time evolution of the system is Deterministic system, deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time), such a system has six degrees of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are not interchangeable; they are commonly distinguished by their position in an ordered tuple, or by a label, such as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the '' number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational–vibrational Coupling
In physics, rotational–vibrational coupling occurs when the angular frequency, rotation frequency of a physical system, system is close to or identical to a natural frequency of internal vibration. The animation on the right shows ideal motion, with the force exerted by the spring (device), spring and the distance from the rotation around a fixed axis, center of rotation increasing together linearly with no friction. In rotational-vibrational coupling, angular velocity oscillates. By pulling the circling masses closer together, the spring transfers its stored strain energy into the kinetic energy of the circling masses, increasing their angular velocity. The spring cannot bring the circling masses together, since the spring's pull weakens as the circling masses approach. At some point, the increasing angular velocity of the circling masses overcomes the pull of the spring, causing the circling masses to increasingly distance themselves. This increasingly strains the spring, str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas State
Gas is a state of matter that has neither a fixed volume nor a fixed shape and is a compressible fluid. A ''pure gas'' is made up of individual atoms (e.g. a noble gas like neon) or molecules of either a single type of atom ( elements such as oxygen) or from different atoms ( compounds such as carbon dioxide). A ''gas mixture'', such as air, contains a variety of pure gases. What distinguishes gases from liquids and solids is the vast separation of the individual gas particles. This separation can make some gases invisible to the human observer. The gaseous state of matter occurs between the liquid and plasma states, the latter of which provides the upper-temperature boundary for gases. Bounding the lower end of the temperature scale lie degenerative quantum gases which are gaining increasing attention. High-density atomic gases super-cooled to very low temperatures are classified by their statistical behavior as either Bose gases or Fermi gases. For a comprehensive listing of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Electronic Transition
In theoretical chemistry, molecular electronic transitions take place when electrons in a molecule are excited from one energy level to a higher energy level. The energy change associated with this transition provides information on the structure of the molecule and determines many of its properties, such as colour. The relationship between the energy involved in the electronic transition and the frequency of radiation is given by Planck's relation. Organic molecules and other molecules The electronic transitions in organic compounds and some other compounds can be determined by ultraviolet–visible spectroscopy, provided that transitions in the ultraviolet (UV) or visible range of the electromagnetic spectrum exist for the compound. Electrons occupying a HOMO (highest-occupied molecular orbital) of a sigma bond (σ) can get excited to the LUMO (lowest-unoccupied molecular orbital) of that bond. This process is denoted as a transition. Likewise, promotion of an electron from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibronic Transition
Vibronic spectroscopy is a branch of molecular spectroscopy concerned with vibronic transitions: the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. In the gas phase, vibronic transitions are also accompanied by changes in rotational energy. Vibronic spectra of diatomic molecules have been analysed in detail; emission spectra are more complicated than absorption spectra. The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. Vibronic spectroscopy may provide information, such as bond length, on electronic excited states of stable molecules. It has also been applied to the study of unstable molecules such as dicarbon (C2) in discharges, flames and astronomical objects.Hollas, p. 211. Principles Electronic transitions are typically observed in the visible and ultraviolet regions, in the wavelength range approximately 200–700&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centrosymmetry
In crystallography, a centrosymmetric point group contains an inversion center as one of its symmetry elements. In such a point group, for every point (x, y, z) in the unit cell there is an indistinguishable point (-x, -y, -z). Such point groups are also said to have ''inversion'' symmetry. Point reflection is a similar term used in geometry. Crystals with an inversion center cannot display certain properties, such as the piezoelectric effect and the frequency doubling effect (second-harmonic generation). In addition, in such crystals, one-photon absorption (OPA) and two-photon absorption (TPA) processes are mutually exclusive, i.e., they do not occur simultaneously, and provide complementary information. The following space groups have inversion symmetry: the triclinic space group 2, the monoclinic 10-15, the orthorhombic 47-74, the tetragonal 83-88 and 123-142, the trigonal 147, 148 and 162-167, the hexagonal 175, 176 and 191-194, the cubic 200-206 and 221-230. Point gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |