|
Molecular Physics
Molecular physics is the study of the physical properties of molecules and molecular dynamics. The field overlaps significantly with physical chemistry, chemical physics, and quantum chemistry. It is often considered as a sub-field of atomic, molecular, and optical physics. Research groups studying molecular physics are typically designated as one of these other fields. Molecular physics addresses phenomena due to both molecular structure and individual atomic processes within molecules. Like atomic physics, it relies on a combination of classical and quantum mechanics to describe interactions between electromagnetic radiation and matter. Experiments in the field often rely heavily on techniques borrowed from atomic physics, such as spectroscopy and scattering. Molecular structure In a molecule, both the electrons and nuclei experience similar-scale forces from the Coulomb interaction. However, the nuclei remain at nearly fixed locations in the molecule while the electrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Scattering
Neutron scattering, the irregular dispersal of free neutrons by matter, can refer to either the naturally occurring physical process itself or to the man-made experimental techniques that use the natural process for investigating materials. The natural/physical phenomenon is of elemental importance in nuclear engineering and the nuclear sciences. Regarding the experimental technique, understanding and manipulating neutron scattering is fundamental to the applications used in crystallography, physics, physical chemistry, biophysics, and materials research. Neutron scattering is practiced at research reactors and spallation neutron sources that provide neutron radiation of varying intensities. Neutron diffraction (elastic scattering) techniques are used for analyzing structures; where inelastic neutron scattering is used in studying atomic vibrations and other excitations. Scattering of fast neutrons "Fast neutrons" (see neutron temperature) have a kinetic energy abo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
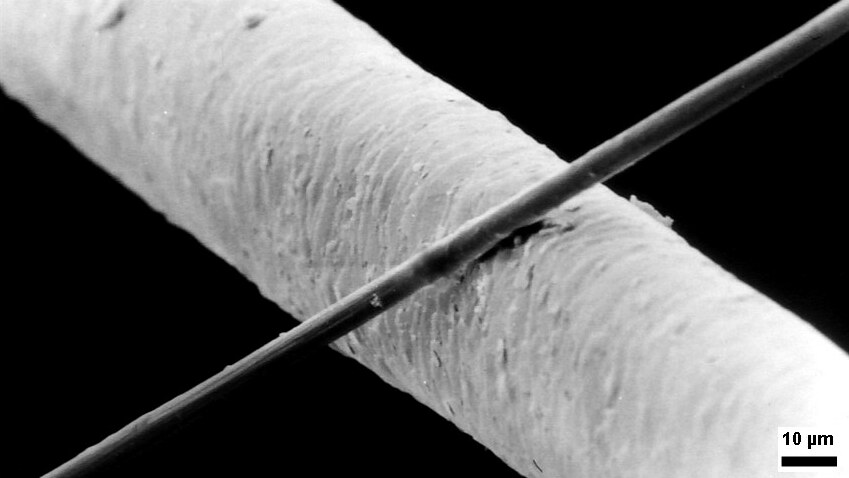
Micrometre
The micrometre (English in the Commonwealth of Nations, Commonwealth English as used by the International Bureau of Weights and Measures; SI symbol: μm) or micrometer (American English), also commonly known by the non-SI term micron, is a unit of length in the International System of Units (SI) equalling (SI standard prefix "micro-" = ); that is, one millionth of a metre (or one thousandth of a millimetre, , or about ). The nearest smaller common SI Unit, SI unit is the nanometre, equivalent to one thousandth of a micrometre, one millionth of a millimetre or one billionth of a metre (). The micrometre is a common unit of measurement for wavelengths of infrared radiation as well as sizes of biological cell (biology), cells and bacteria, and for grading wool by the diameter of the fibres. The width of a single human hair ranges from approximately 20 to . Examples Between 1 μm and 10 μm: * 1–10 μm – length of a typical bacterium * 3–8 μm – width of str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infrared
Infrared (IR; sometimes called infrared light) is electromagnetic radiation (EMR) with wavelengths longer than that of visible light but shorter than microwaves. The infrared spectral band begins with the waves that are just longer than those of red light (the longest waves in the visible spectrum), so IR is invisible to the human eye. IR is generally (according to ISO, CIE) understood to include wavelengths from around to . IR is commonly divided between longer-wavelength thermal IR, emitted from terrestrial sources, and shorter-wavelength IR or near-IR, part of the solar spectrum. Longer IR wavelengths (30–100 μm) are sometimes included as part of the terahertz radiation band. Almost all black-body radiation from objects near room temperature is in the IR band. As a form of EMR, IR carries energy and momentum, exerts radiation pressure, and has properties corresponding to both those of a wave and of a particle, the photon. It was long known that fires e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Potential
Electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as electric potential energy per unit of electric charge. More precisely, electric potential is the amount of work (physics), work needed to move a test charge from a reference point to a specific point in a static electric field. The test charge used is small enough that disturbance to the field is unnoticeable, and its motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is Earth (electricity), earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar (physics), scalar quantity denoted by or occasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known. One-dimensional harmonic oscillator Hamiltonian and energy eigenstates The Hamiltonian of the particle is: \hat H = \frac + \frac k ^2 = \frac + \frac m \omega^2 ^2 \, , where is the particle's mass, is the force constant, \omega = \sqrt is the angular frequency of the oscillator, \hat is the position operator (given by in the coordinate basis), and \hat is the momentum operator (given by \hat p = -i \hbar \, \partial / \partial x in the coordinate basis). The first term in the Hamiltonian represents the kinetic energy of the particle, and the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantization (physics)
Quantization (in British English quantisation) is the systematic transition procedure from a classical understanding of physical phenomena to a newer understanding known as quantum mechanics. It is a procedure for constructing quantum mechanics from classical mechanics. A generalization involving infinite degrees of freedom is field quantization, as in the "quantization of the electromagnetic field", referring to photons as field " quanta" (for instance as light quanta). This procedure is basic to theories of atomic physics, chemistry, particle physics, nuclear physics, condensed matter physics, and quantum optics. Historical overview In 1901, when Max Planck was developing the distribution function of statistical mechanics to solve the ultraviolet catastrophe problem, he realized that the properties of blackbody radiation can be explained by the assumption that the amount of energy must be in countable fundamental units, i.e. amount of energy is not continuous but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Spectrum
The electromagnetic spectrum is the full range of electromagnetic radiation, organized by frequency or wavelength. The spectrum is divided into separate bands, with different names for the electromagnetic waves within each band. From low to high frequency these are: radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays. The electromagnetic waves in each of these bands have different characteristics, such as how they are produced, how they interact with matter, and their practical applications. Radio waves, at the low-frequency end of the spectrum, have the lowest photon energy and the longest wavelengths—thousands of kilometers, or more. They can be emitted and received by antenna (radio), antennas, and pass through the atmosphere, foliage, and most building materials. Gamma rays, at the high-frequency end of the spectrum, have the highest photon energies and the shortest wavelengths—much smaller than an atomic nucleus. Gamma rays, X-rays, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultraviolet
Ultraviolet radiation, also known as simply UV, is electromagnetic radiation of wavelengths of 10–400 nanometers, shorter than that of visible light, but longer than X-rays. UV radiation is present in sunlight and constitutes about 10% of the total electromagnetic radiation output from the Sun. It is also produced by electric arcs, Cherenkov radiation, and specialized lights, such as mercury-vapor lamps, tanning lamps, and black lights. The photons of ultraviolet have greater energy than those of visible light, from about 3.1 to 12 electron volts, around the minimum energy required to ionize atoms. Although long-wavelength ultraviolet is not considered an ionizing radiation because its photons lack sufficient energy, it can induce chemical reactions and cause many substances to glow or fluoresce. Many practical applications, including chemical and biological effects, are derived from the way that UV radiation can interact with organic molecules. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Volts
In physics, an electronvolt (symbol eV), also written electron-volt and electron volt, is the measure of an amount of kinetic energy gained by a single electron accelerating through an electric potential difference of one volt in vacuum. When used as a unit of energy, the numerical value of 1 eV in joules (symbol J) is equal to the numerical value of the charge of an electron in coulombs (symbol C). Under the 2019 revision of the SI, this sets 1 eV equal to the exact value Historically, the electronvolt was devised as a standard unit of measure through its usefulness in electrostatic particle accelerator sciences, because a particle with electric charge ''q'' gains an energy after passing through a voltage of ''V''. Definition and use An electronvolt is the amount of energy gained or lost by a single electron when it moves through an electric potential difference of one volt. Hence, it has a value of one volt, which is , multiplied by the elementary charge Therefore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Planck Constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation. Planck later referred to the constant as the "quantum of action". In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, when the Pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Orbital
In quantum mechanics, an atomic orbital () is a Function (mathematics), function describing the location and Matter wave, wave-like behavior of an electron in an atom. This function describes an electron's Charge density, charge distribution around the Atomic nucleus, atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus. Each orbital in an atom is characterized by a set of values of three quantum numbers , , and , which respectively correspond to electron's energy, its angular momentum, orbital angular momentum, and its orbital angular momentum projected along a chosen axis (magnetic quantum number). The orbitals with a well-defined magnetic quantum number are generally complex-valued. Real-valued orbitals can be formed as linear combinations of and orbitals, and are often labeled using associated Spherical harmonics#Harmonic polynomial representation, harmonic polynomials (e.g., ''xy'', ) which describe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |