|
Minimum Mean-square Error
In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter. Motivation The term MMSE more specifically refers to estimation in a Bayesian setting with quadratic cost function. The basic idea behind the Bayesian approach to estimation stem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Information
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable ''X'' carries about an unknown parameter ''θ'' of a distribution that models ''X''. Formally, it is the variance of the score, or the expected value of the observed information. The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized and explored by the statistician Sir Ronald Fisher (following some initial results by Francis Ysidro Edgeworth). The Fisher information matrix is used to calculate the covariance matrices associated with maximum-likelihood estimates. It can also be used in the formulation of test statistics, such as the Wald test. In Bayesian statistics, the Fisher information plays a role in the derivation of non-informative prior distributions according to Jeffreys' rule. It also appears as the large-sample covariance of the posterior distribution, provided that the prior i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levinson Recursion
Levinson recursion or Levinson–Durbin recursion is a procedure in linear algebra to recursively calculate the solution to an equation involving a Toeplitz matrix. The algorithm runs in time, which is a strong improvement over Gauss–Jordan elimination, which runs in Θ(''n''3). The Levinson–Durbin algorithm was proposed first by Norman Levinson in 1947, improved by James Durbin in 1960, and subsequently improved to and then multiplications by W. F. Trench and S. Zohar, respectively. Other methods to process data include Schur decomposition and Cholesky decomposition. In comparison to these, Levinson recursion (particularly split Levinson recursion) tends to be faster computationally, but more sensitive to computational inaccuracies like round-off errors. The Bareiss algorithm for Toeplitz matrices (not to be confused with the general Bareiss algorithm) runs about as fast as Levinson recursion, but it uses space, whereas Levinson recursion uses only ''O''(''n'') space. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient Method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cholesky Decomposition
In linear algebra, the Cholesky decomposition or Cholesky factorization (pronounced ) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations. Statement The Cholesky decomposition of a Hermitian positive-definite matrix , is a decomposition of the form \mathbf = \mathbf^, where is a lower triangular matrix with real and positive diagonal entries, and * denotes the conjugate transpose of . Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. The converse holds trivially: if can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
QR Decomposition
In linear algebra, a QR decomposition, also known as a QR factorization or QU factorization, is a decomposition of a matrix ''A'' into a product ''A'' = ''QR'' of an orthonormal matrix ''Q'' and an upper triangular matrix ''R''. QR decomposition is often used to solve the linear least squares (LLS) problem and is the basis for a particular eigenvalue algorithm, the QR algorithm. Cases and definitions Square matrix Any real square matrix ''A'' may be decomposed as : A = QR, where ''Q'' is an orthogonal matrix (its columns are orthogonal unit vectors meaning and ''R'' is an upper triangular matrix (also called right triangular matrix). If ''A'' is invertible, then the factorization is unique if we require the diagonal elements of ''R'' to be positive. If instead ''A'' is a complex square matrix, then there is a decomposition ''A'' = ''QR'' where ''Q'' is a unitary matrix (so the conjugate transpose If ''A'' has ''n'' linearly independent columns, then the first ''n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss Elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of row-wise operations performed on the corresponding matrix of coefficients. This method can also be used to compute the rank of a matrix, the determinant of a square matrix, and the inverse of an invertible matrix. The method is named after Carl Friedrich Gauss (1777–1855). To perform row reduction on a matrix, one uses a sequence of elementary row operations to modify the matrix until the lower left-hand corner of the matrix is filled with zeros, as much as possible. There are three types of elementary row operations: * Swapping two rows, * Multiplying a row by a nonzero number, * Adding a multiple of one row to another row. Using these operations, a matrix can always be transformed into an upper triangular matrix (possibly bordered by rows or columns of zeros), and in fact one that is in row echelon form. Once all of the leading ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson's Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Posterior Probability
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posterior probability contains everything there is to know about an uncertain proposition (such as a scientific hypothesis, or parameter values), given prior knowledge and a mathematical model describing the observations available at a particular time. After the arrival of new information, the current posterior probability may serve as the prior in another round of Bayesian updating. In the context of Bayesian statistics, the posterior probability distribution usually describes the epistemic uncertainty about statistical parameters conditional on a collection of observed data. From a given posterior distribution, various point and interval estimates can be derived, such as the maximum a posteriori (MAP) or the highest posterior density int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
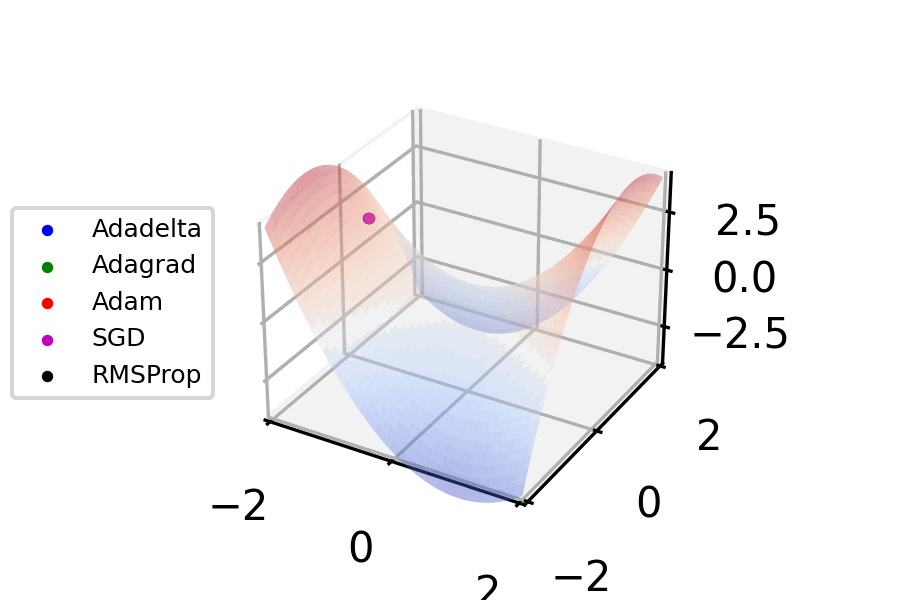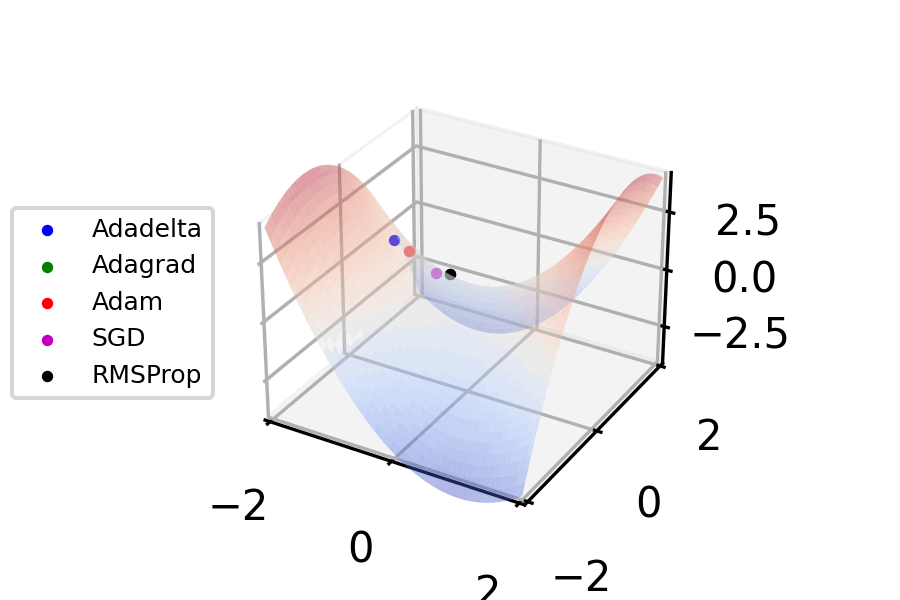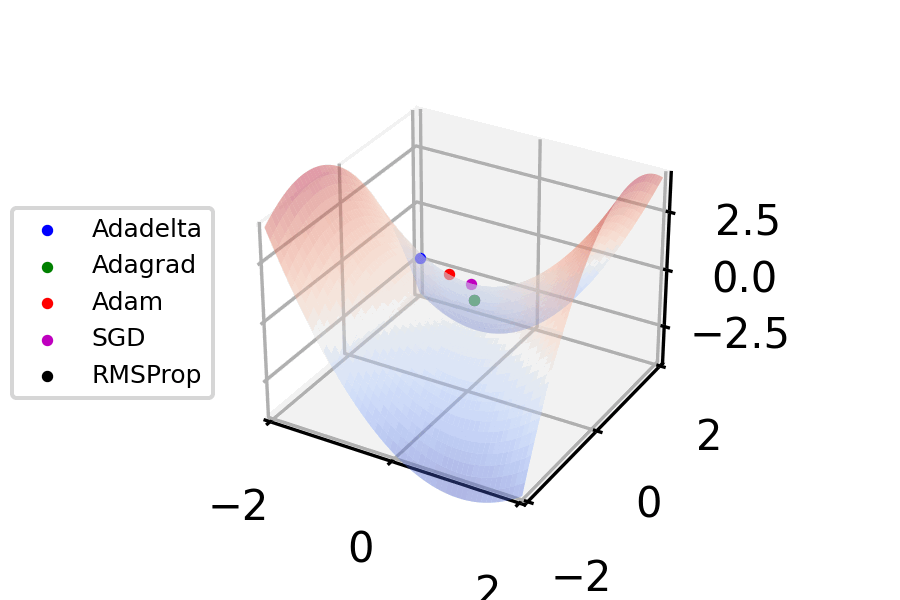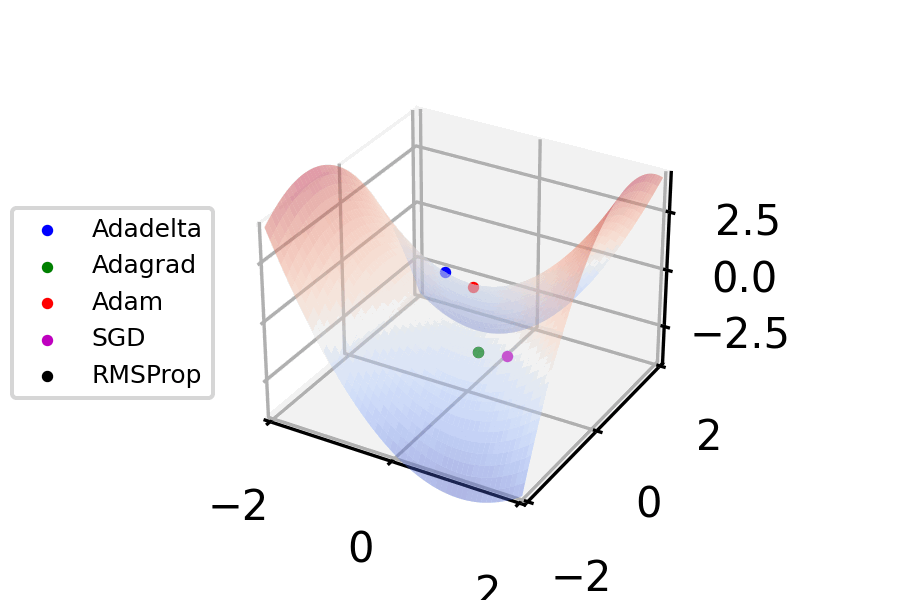
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) is a class of algorithms used to draw samples from a probability distribution. Given a probability distribution, one can construct a Markov chain whose elements' distribution approximates it – that is, the Markov chain's Discrete-time Markov chain#Stationary distributions, equilibrium distribution matches the target distribution. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Markov chain Monte Carlo methods are used to study probability distributions that are too complex or too highly N-dimensional space, dimensional to study with analytic techniques alone. Various algorithms exist for constructing such Markov chains, including the Metropolis–Hastings algorithm. General explanation Markov chain Monte Carlo methods create samples from a continuous random variable, with probability density proportional to a known function. These samples can be used to e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jointly Gaussian
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathbf i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |