|
Median Voter Theorem
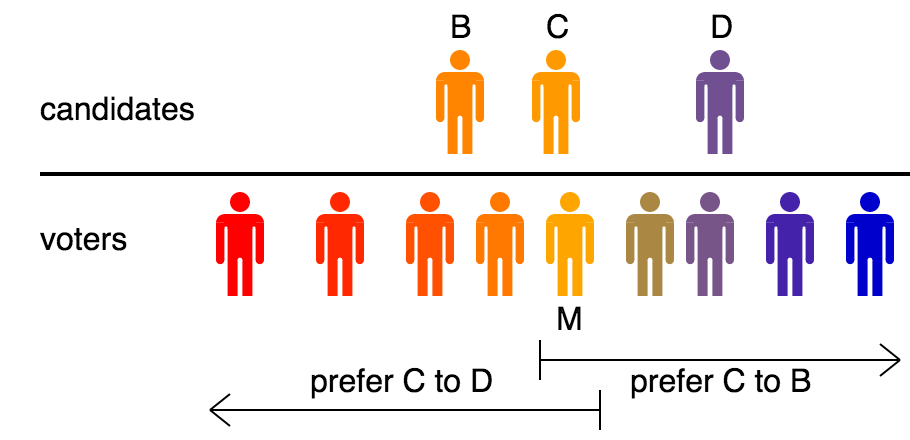
In political science and social choice theory, social choice, Black's median voter theorem says that if voters and candidates are distributed along a political spectrum, any voting method Condorcet criterion, compatible with majority-rule will elect the candidate preferred by the median voter. The median voter theorem thus shows that under a realistic model of voter behavior, Arrow's impossibility theorem, Arrow's theorem does not apply, and Decision theory, rational choice is possible for societies. The theorem was first derived by Duncan Black in 1948, and independently by Kenneth Arrow. Voting rules without this median voter property, like Instant-runoff voting, ranked choice voting, Plurality voting, plurality, and plurality-with-primaries have a Center-squeeze, center-squeeze effect that encourages candidates to take more extreme positions than the population would prefer. Similar median voter theorems exist for rules like score voting and approval voting when voters are either ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Political Science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, political behavior, and associated constitutions and laws. Specialists in the field are political scientists. History Origin Political science is a social science dealing with systems of governance and power, and the analysis of political activities, political institutions, political thought and behavior, and associated constitutions and laws. As a social science, contemporary political science started to take shape in the latter half of the 19th century and began to separate itself from political philosophy and history. Into the late 19th century, it was still uncommon for political science to be considered a distinct field from history. The term "political science" was not always distinguished from political philosophy, and the modern dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Corollary
In mathematics and logic, a corollary ( , ) is a theorem of less importance which can be readily deduced from a previous, more notable statement. A corollary could, for instance, be a proposition which is incidentally proved while proving another proposition; it might also be used more casually to refer to something which naturally or incidentally accompanies something else. Overview In mathematics, a corollary is a theorem connected by a short proof to an existing theorem. The use of the term ''corollary'', rather than ''proposition'' or ''theorem'', is intrinsically subjective. More formally, proposition ''B'' is a corollary of proposition ''A'', if ''B'' can be readily deduced from ''A'' or is self-evident from its proof. In many cases, a corollary corresponds to a special case of a larger theorem, which makes the theorem easier to use and apply, even though its importance is generally considered to be secondary to that of the theorem. In particular, ''B'' is unlikely to be te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donald Saari
Donald Gene Saari (born March 1940) is an American mathematician, a Distinguished Professor of Mathematics and Economics and former director of the Institute for Mathematical Behavioral Sciences at the University of California, Irvine. His research interests include the -body problem, the Borda count voting system, and application of mathematics to the social sciences. Contributions Saari has been widely quoted as an expert in voting systems and lottery odds. He is opposed to the use of the Condorcet criterion in evaluating voting systems, and among positional voting schemes he favors using the Borda count over plurality voting, because it reduces the frequency of paradoxical outcomes (which however cannot be avoided entirely in ranking systems because of Arrow's impossibility theorem). For instance, as he has pointed out, plurality voting can lead to situations where the election outcome would remain unchanged if all voters' preferences were reversed; this cannot happen with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borda Count
The Borda method or order of merit is a positional voting rule that gives each candidate a number of points equal to the number of candidates ranked below them: the lowest-ranked candidate gets 0 points, the second-lowest gets 1 point, and so on. The candidate with the most points wins. The Borda count has been independently reinvented several times, with the first recorded proposal in 1435 being by Nicholas of Cusa (see History below), but is named after the 18th-century French mathematician and naval engineer Jean-Charles de Borda, who re-devised the system in 1770. The Borda count is well-known in social choice theory both for its pleasant theoretical properties and its ease of manipulation. In the absence of strategic voting and strategic nomination, the Borda count tends to elect broadly-acceptable options or candidates (rather than consistently following the preferences of a majority); when both voting and nomination patterns are completely random, the Borda count gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marquis De Condorcet
Marie Jean Antoine Nicolas de Caritat, Marquis of Condorcet (; ; 17 September 1743 – 29 March 1794), known as Nicolas de Condorcet, was a French Philosophy, philosopher, Political economy, political economist, Politics, politician, and mathematician. His ideas, including support for liberal economy, free markets, Universal access to education, public education, constitutionalism, constitutional government, and Social equality, equal rights for women and people of all races, have been said to embody the ideals of the Age of Enlightenment, of which he has been called the "last witness", and Enlightenment rationalism. A critic of the constitution proposed by Marie-Jean Hérault de Séchelles in 1793, the Convention Nationale – and the Jacobin faction in particular – voted to have Condorcet arrested. He died in prison after a period of hiding from the French Revolutionary authorities. Early years Condorcet was born in Ribemont (in present-day Aisne), descended ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Model Of Voting
In political science and social choice theory, the spatial (sometimes ideological or ideal-point) model of voting, also known as the Hotelling–Downs model, is a mathematical model of voting behavior. It describes voters and candidates as varying along one or more axes (or dimensions), where each axis represents an attribute of the candidate that voters care about. Voters are modeled as having an ideal point in this space and preferring candidates closer to this point over those who are further away; these kinds of preferences are called single-peaked. The most common example of a spatial model is a political spectrum or compass, such as the traditional left-right axis, but issue spaces can be more complex. For example, a study of German voters found at least four dimensions were required to adequately represent all political parties. Besides ideology, a dimension can represent any attribute of the candidates, such as their views on one particular issue. It can also represen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coombs' Method
Coombs' method is a ranked voting system. Like instant-runoff (IRV-RCV), Coombs' method is a sequential-loser method, where the last-place finisher according to one method is eliminated in each round. However, unlike in instant-runoff, each round has electors voting against their least-favorite candidate; the candidate ranked last by the most voters is eliminated. The method fails several voting system criteria, including Condorcet's majority criterion, monotonicity, participation, and clone-independence. However, it does satisfy Black's single-peaked median voter criterion. History The method was popularized by Clyde Coombs. It was described by Edward J. Nanson as the "Venetian method" (which should not be confused with the Republic of Venice's use of score voting in elections for Doge). Procedures Each voter rank-orders all of the candidates on their ballot. Otherwise, the candidate ranked last by the largest number ( plurality) of voters is eliminated, making eac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Valence Politics
Valence or valency may refer to: Science *Valence (chemistry), a measure of an element's combining power with other atoms * Valence electron, electrons in the outer shell of an atom's energy levels *Valence quarks, those quarks within a hadron that determine the hadron's quantum numbers * Degree (graph theory), also called the valency of a vertex in graph theory *Valency (linguistics), aspect of verbs relative to other parts of speech * Valence (psychology) or hedonic tone, the (emotional) value associated with an event, object or situation Places France * Valence, Charente, a commune in the Charente department * Valence, Drôme, Drôme, a commune and prefecture of the Drôme department ** University of Valence, a medieval university * Valence, Tarn-et-Garonne, a commune in the Tarn-et-Garonne department * Canton of Valence, Tarn-et-Garonne department * Arrondissement of Valence, Drôme department * Roman Catholic Diocese of Valence * Valence-d'Albigeois, in the Tarn depa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single Peaked Preferences
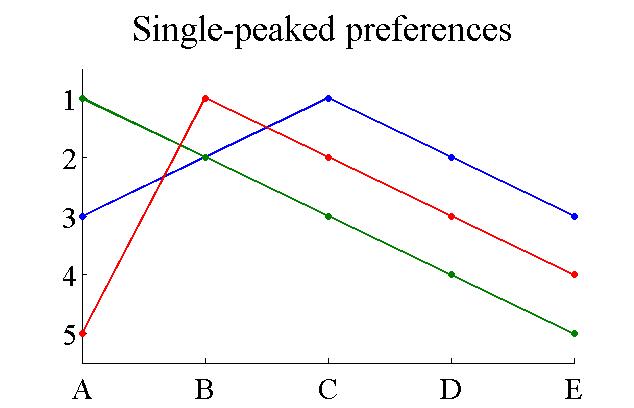
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of Public good (economics), public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the Monotonicity (mechani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majority Vote
A majority is more than half of a total; however, the term is commonly used with other meanings, as explained in the "#Related terms, Related terms" section below. It is a subset of a Set (mathematics), set consisting of more than half of the set's elements. For example, if a group consists of 31 individuals, a majority would be 16 or more individuals, while having 15 or fewer individuals would not constitute a majority. A majority is different from, but often confused with, a Plurality (voting), plurality, which is a subset larger than any other subset but not necessarily more than half the set. See the "#Related terms, Related terms" section below for details. Majority vote In parliamentary procedure, a majority always means precisely "more than half". Other common definitions (e.g. the frequent 50%+1) may be misleading #Common errors, (see "Common errors" below). Depending on the parliamentary authority used, there may be a difference in the total that is used to calculat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Winner
A Condorcet winner (, ) is a candidate who would receive the support of more than half of the electorate in a one-on-one race against any one of their opponents. Voting systems where a majority winner will always win are said to satisfy the Condorcet winner criterion. The Condorcet winner criterion extends the principle of majority rule to elections with multiple candidates. Named after Nicolas de Condorcet, it is also called a majority winner, a majority-preferred candidate, a beats-all winner, or tournament winner (by analogy with round-robin tournaments). A Condorcet winner may not necessarily always exist in a given electorate: it is possible to have a rock, paper, scissors-style cycle, when multiple candidates defeat each other (Rock < Paper < Scissors < Rock). This is called , and is analogous to the counterintuitive [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |