|
Mechanical Properties Of Biomaterials
Materials that are used for biomedical or clinical applications are known as biomaterials. The following article deals with fifth generation biomaterials that are used for bone structure replacement. For any material to be classified for biomedical applications, three requirements must be met. The first requirement is that the material must be biocompatible; it means that the organism should not treat it as a foreign object. Secondly, the material should be biodegradable (for in-graft only); the material should harmlessly degrade or dissolve in the body of the organism to allow it to resume natural functioning. Thirdly, the material should be mechanically sound; for the replacement of load-bearing structures, the material should possess equivalent or greater mechanical stability to ensure high reliability of the graft. Introduction The biomaterial term is used for materials that can be used in biomedical and clinical applications. They are bioactive and biocompatible in nature. Curr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biomedical
Biomedicine (also referred to as Western medicine, mainstream medicine or conventional medicine)Biomedicine " NCI Dictionary of Cancer Medicine. . is a branch of that applies biological and physiological principles to . Biomedicine stresses standardized, evidence-based treatment validated through biological research, with treatment administered via formally tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the Stress (mechanics), stress in a material just before it Yield (engineering), yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the Elasticity (physics), elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the Pascal (unit), pascal (Pa), although it is usually expressed in Pascal (unit), gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional analysis, dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (mechanics)
In physics and continuum mechanics, deformation is the change in the shape (geometry), shape or size of an object. It has dimension (physics), dimension of length with SI unit of metre (m). It is quantified as the residual displacement (geometry), displacement of particles in a non-rigid body, from an configuration to a configuration, excluding the body's average translation (physics), translation and rotation (its rigid transformation). A ''configuration'' is a set containing the position (geometry), positions of all particles of the body. A deformation can occur because of structural load, external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. In a continuous body, a ''deformation field'' results from a Stress (physics), stress field due to applied forces or because of some changes in the conditions of the body. The relation between stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biomaterials
A biomaterial is a substance that has been engineered to interact with biological systems for a medical purpose – either a therapeutic (treat, augment, repair, or replace a tissue function of the body) or a diagnostic one. The corresponding field of study, called biomaterials science or biomaterials engineering, is about fifty years old. It has experienced steady growth over its history, with many companies investing large amounts of money into the development of new products. Biomaterials science encompasses elements of medicine, biology, chemistry, tissue engineering and materials science. A biomaterial is different from a biological material, such as bone, that is produced by a biological system. However, "biomaterial" and "biological material" are often used interchangeably. Further, the word "bioterial" has been proposed as a potential alternate word for biologically-produced materials such as bone, or fungal biocomposites. Additionally, care should be exercised in defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
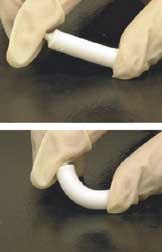
Artificial Bone
Artificial bone refers to bone-like material created in a laboratory that can be used in bone grafts, to replace human bone that was lost due to severe fractures, disease, etc. Bone fracture, which is a complete or partial break in the bone, is a very common condition that has more than three million US cases per year. Human bones have the ability to regenerate themselves by cycle of bone resorption and bone formation. The cell responsible for bone resorption is osteoclast, while the cell responsible for bone formation is osteoblast. That being said, the human body can regenerate fractured bone. However, if damage to bone is caused by a disease or severe injury, it becomes difficult for the body to repair itself. When the human body is unable to regenerate the lost bone tissue, surgeons come in and replace the missing bone using autografts, allografts, and synthetic grafts (artificial bone). When comparing artificial bone to autograft and allograft, it is less invasive and more bio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress Relaxation
In materials science, stress relaxation is the observed decrease in stress in response to strain generated in the structure. This is primarily due to keeping the structure in a strained condition for some finite interval of time hence causing some amount of plastic strain. This should not be confused with creep, which is a constant state of stress with an increasing amount of strain. Since relaxation relieves the state of stress, it has the effect of also relieving the equipment reactions. Thus, relaxation has the same effect as cold springing, except it occurs over a longer period of time. The amount of relaxation which takes place is a function of time, temperature and stress level, thus the actual effect it has on the system is not precisely known, but can be bounded. Stress relaxation describes how polymers relieve stress under constant strain. Because they are viscoelastic, polymers behave in a nonlinear, non-Hookean fashion.Meyers and Chawla. "Mechanical Behavior of Mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rheological
Rheology (; ) is the study of the flow of matter, primarily in a fluid (liquid or gas) state but also as "soft solids" or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied forcRheology is the branch of physics that deals with the deformation and flow of materials, both solids and liquids.W. R. Schowalter (1978) Mechanics of Non-Newtonian Fluids Pergamon The term ''rheology'' was coined by Eugene C. Bingham, a professor at Lafayette College, in 1920 from a suggestion by a colleague, Markus Reiner.The Deborah Number The term was inspired by the of |
Linear Elasticity
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics. The fundamental assumptions of linear elasticity are infinitesimal strains — meaning, "small" deformations — and linear relationships between the components of stress and strain — hence the "linear" in its name. Linear elasticity is valid only for stress states that do not produce yielding. Its assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis. Mathematical formulation Equations governing a linear elastic boundary value problem are based on three tensor partial differential equations for the balance of linear momentum and six in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flow Plasticity Theory
Flow plasticity is a solid mechanics theory that is used to describe the plasticity (physics), plastic behavior of materials. Flow plasticity theories are characterized by the assumption that a flow rule (plasticity), flow rule exists that can be used to determine the amount of plastic deformation in the material. In flow plasticity theories it is assumed that the total deformation (mechanics), strain in a body can be decomposed additively (or multiplicatively) into an elastic part and a plastic part. The elastic part of the strain can be computed from a linear elasticity, linear elastic or hyperelastic material, hyperelastic constitutive model. However, determination of the plastic part of the strain requires a flow rule (plasticity), flow rule and a hardening model (plasticity), hardening model. Small deformation theory Typical flow plasticity theories for unidirectional loading (for small deformation perfect plasticity or hardening plasticity) are developed on the basis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |