|
Matrix Regularization
In the field of statistical learning theory, matrix regularization generalizes notions of vector regularization to cases where the object to be learned is a matrix. The purpose of regularization is to enforce conditions, for example sparsity or smoothness, that can produce stable predictive functions. For example, in the more common vector framework, Tikhonov regularization optimizes over : \min_x \, Ax - y\, ^2 + \lambda \, x\, ^2 to find a vector x that is a stable solution to the regression problem. When the system is described by a matrix rather than a vector, this problem can be written as : \min_X \, AX - Y\, ^2 + \lambda \, X\, ^2, where the vector norm enforcing a regularization penalty on x has been extended to a matrix norm on X. Matrix regularization has applications in matrix completion, multivariate regression, and multi-task learning. Ideas of feature and group selection can also be extended to matrices, and these can be generalized to the nonparametric case of mul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Learning Theory
Statistical learning theory is a framework for machine learning drawing from the fields of statistics and functional analysis. Statistical learning theory deals with the statistical inference problem of finding a predictive function based on data. Statistical learning theory has led to successful applications in fields such as computer vision, speech recognition, and bioinformatics. Introduction The goals of learning are understanding and prediction. Learning falls into many categories, including supervised learning, unsupervised learning, online learning, and reinforcement learning. From the perspective of statistical learning theory, supervised learning is best understood. Supervised learning involves learning from a training set of data. Every point in the training is an input-output pair, where the input maps to an output. The learning problem consists of inferring the function that maps between the input and the output, such that the learned function can be used to pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Multivariate Analysis
The ''Journal of Multivariate Analysis'' is a monthly peer-reviewed scientific journal that covers applications and research in the field of multivariate statistical analysis. The journal's scope includes theoretical results as well as applications of new theoretical methods in the field. Some of the research areas covered include copula modeling, functional data analysis, graphical modeling, high-dimensional data analysis, image analysis, multivariate extreme-value theory, sparse modeling, and spatial statistics. According to the ''Journal Citation Reports'', the journal has a 2017 impact factor of 1.009. See also *List of statistics journals This is a list of scientific journals published in the field of statistics. Introductory and outreach *''The American Statistician'' *'' Significance'' General theory and methodology *''Annals of the Institute of Statistical Mathematics'' *''An ... References External links * {{DEFAULTSORT:Journal of Multivariate Analysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimation Theory
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An '' estimator'' attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered: * The probabilistic approach (described in this article) assumes that the measured data is random with probability distribution dependent on the parameters of interest * The set-membership approach assumes that the measured data vector belongs to a set which depends on the parameter vector. Examples For example, it is desired to estimate the proportion of a population of voters who will vote for a particular candidate. That proportion is the parameter sought; the estimate is based on a small random sample of voters. Alternatively, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reproducing Kernel Hilbert Space
In functional analysis (a branch of mathematics), a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Roughly speaking, this means that if two functions f and g in the RKHS are close in norm, i.e., \, f-g\, is small, then f and g are also pointwise close, i.e., , f(x)-g(x), is small for all x. The converse does not need to be true. Informally, this can be shown by looking at the supremum norm: the sequence of functions \sin^n (x) converges pointwise, but do not converge uniformly i.e. do not converge with respect to the supremum norm (note that this is not a counterexample because the supremum norm does not arise from any inner product due to not satisfying the parallelogram law). It is not entirely straightforward to construct a Hilbert space of functions which is not an RKHS. Some examples, however, have been found. Note that ''L''2 spaces are not Hilbert spaces of functions (and hence not R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Selection
In machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features (variables, predictors) for use in model construction. Feature selection techniques are used for several reasons: :* simplification of models to make them easier to interpret by researchers/users, :* shorter training times, :* to avoid the curse of dimensionality, :*improve data's compatibility with a learning model class, :*encode inherent symmetries present in the input space. The central premise when using a feature selection technique is that the data contains some features that are either ''redundant'' or ''irrelevant'', and can thus be removed without incurring much loss of information. ''Redundant'' and ''irrelevant'' are two distinct notions, since one relevant feature may be redundant in the presence of another relevant feature with which it is strongly correlated. Feature sele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proximal Gradient Method
Proximal gradient methods are a generalized form of projection used to solve non-differentiable convex optimization problems. Many interesting problems can be formulated as convex optimization problems of the form \operatorname\limits_ \sum_^n f_i(x) where f_i: \mathbb^N \rightarrow \mathbb,\ i = 1, \dots, n are possibly non-differentiable convex functions. The lack of differentiability rules out conventional smooth optimization techniques like the steepest descent method and the conjugate gradient method, but proximal gradient methods can be used instead. Proximal gradient methods starts by a splitting step, in which the functions f_1, . . . , f_n are used individually so as to yield an easily implementable algorithm. They are called proximal because each non-differentiable function among f_1, . . . , f_n is involved via its proximity operator. Iterative shrinkage thresholding algorithm, projected Landweber, projected gradient, alternating projections, alternating- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
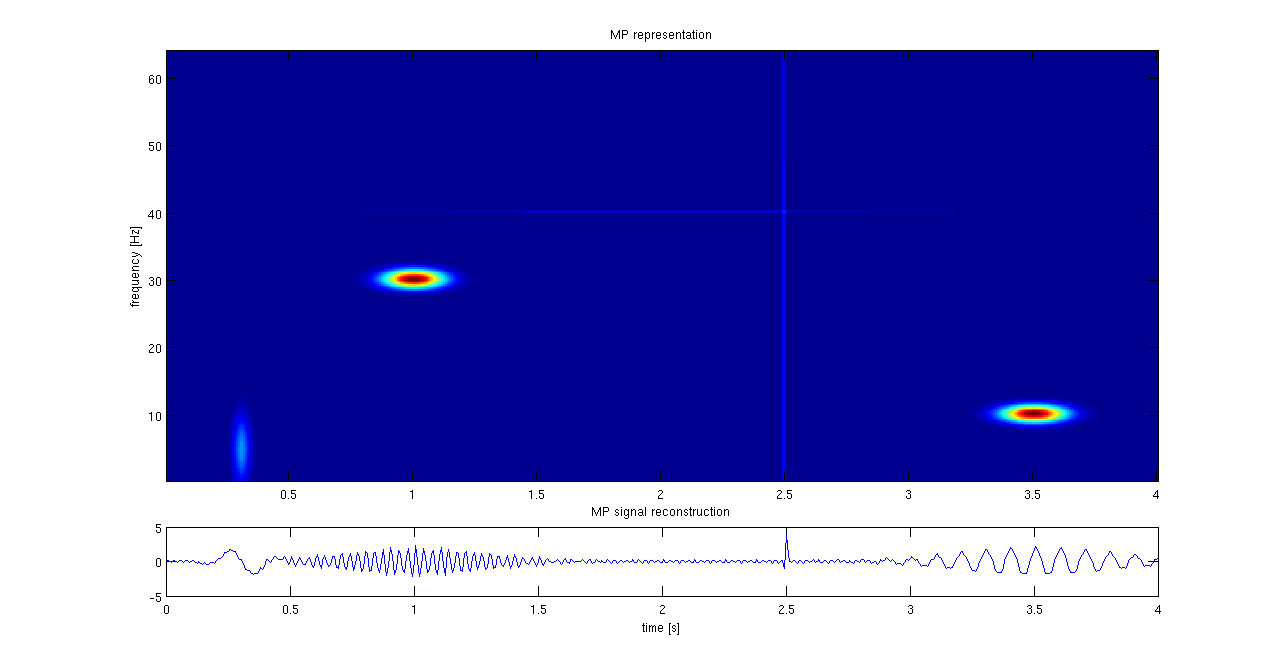
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactorily d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning (journal)
''Machine Learning'' is a peer-reviewed scientific journal, published since 1986. In 2001, forty editors and members of the editorial board of ''Machine Learning'' resigned in order to support the ''Journal of Machine Learning Research'' (JMLR), saying that in the era of the internet, it was detrimental for researchers to continue publishing their papers in expensive journals with pay-access archives. Instead, they wrote, they supported the model of ''JMLR'', in which authors retained copyright over their papers and archives were freely available on the internet. Following the mass resignation, Kluwer changed their publishing policy to allow authors to self-archive their papers online after peer-review Peer review is the evaluation of work by one or more people with similar competencies as the producers of the work (peers). It functions as a form of self-regulation by qualified members of a profession within the relevant field. Peer review .... Selected articles * * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso (statistics)
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso or LASSO) is a regression analysis method that performs both variable selection and regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear. Though originally defined for linear regression, lasso regularization is easily extended to other statistical models including generalized linear models, g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schatten Norm
In mathematics, specifically functional analysis, the Schatten norm (or Schatten–von-Neumann norm) arises as a generalization of ''p''-integrability similar to the trace class norm and the Hilbert–Schmidt norm. Definition Let H_1, H_2 be Hilbert spaces, and T a (linear) bounded operator from H_1 to H_2. For p\in T\, _ = [\mathrm (, T, ^p). If T is compact and H_1,\,H_2 are separable, then : \, T\, _ := \bigg( \sum _ s^p_n(T)\bigg)^ for s_1(T) \ge s_2(T) \ge \cdots s_n(T) \ge \cdots \ge 0 the singular values of T, i.e. the eigenvalues of the Hermitian operator , T, :=\sqrt. Properties In the following we formally extend the range of p to ,\infty/math> with the convention that \, \cdot\, _ is the operator norm. The dual index to p=\infty is then q=1. * The Schatten norms are unitarily invariant: for unitary operators U and V and p\in ,\infty/math>, :: \, U T V\, _p = \, T\, _p. * They satisfy Hölder's inequality: for all p\in ,\infty/math> and q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tikhonov Regularization
Ridge regression is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. Also known as Tikhonov regularization, named for Andrey Tikhonov, it is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias (see bias–variance tradeoff). The theory was first introduced by Hoerl and Kennard in 1970 in their '' Technometrics'' papers “RIDGE regressions: biased estimation of nonorthogonal problems” and “RIDGE regressions: applications in nonorthogonal problems”. This was the result of ten years of research into the field of ridge a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |